Butterfly network
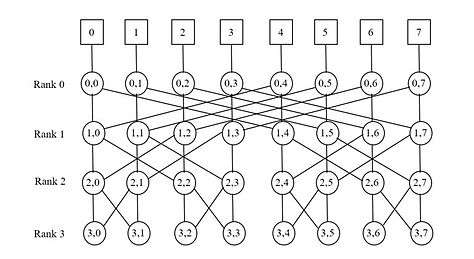
A butterfly network is a multistage interconnection network topology, which can be used to connect different nodes in a multiprocessor system. The interconnect network for a shared memory multiprocessor systems needs to have low latency and high bandwidth compared to other network systems, like local area networks (LANs) or internet.[1] There are three reasons for the needs of low latency and high banwidth in multiprocessor systems: (1) Messages are relatively short as most messages consist of coherence protocol requests and responses without data. (2) Messages are generated frequently because each read or write miss generates messages to every node in the system to ensure coherence. Read or write misses occur when the requested data is not in the processors cache and need to be fetched from either memory or another processor's cache. (3) Messages are generated frequently, therefore rendering it difficult for processors to hide the communication delay.
The major components of an interconnect network are:[2]
- Processor Nodes which consist of one or more processors along with their caches, memories and communication assist.
- Switching Nodes (Router) which connect communication assist of different processor nodes in a system. In multistage topologies, higher level switching nodes connect to lower level switching nodes as shown in figure 1, where switching nodes in rank 0 connect to processor nodes directly while switching nodes in rank 1 connect to switching nodes in rank 0.
- Link which are physical wires between two switching nodes (routers). They can be uni-directional or bi-directional.
These multistage networks have lower cost than a cross bar but still obtain lower contention than a bus. Also the ratio of switching nodes to processor nodes is greater than one in a butterfly network. Such topology where the ratio of switching nodes to processor nodes is greater than one is called an indirect topology.[3]
The network derived its name from connections between nodes in two adjacent ranks (as shown in figure 1), which resembles a butterfly. When top and bottom ranks are merged into a single rank, it is called a Wrapped Butterfly Network.[3] In figure 1, if rank 3 nodes are connected back to respective rank 0 nodes, then it becomes a wrapped butterfly network.
BBN Butterfly, a massive parallel computer built by Bolt, Beranek and Newman in the 1980s, used butterfly interconnect network.[4] Also, Cray machine Cray C90, used butterfly network to communicate between its 16 processors and 1024 memory banks.[5]
Butterfly network building[3]
For a butterfly network with 'p' processor nodes, there needs to be p(log2 p + 1) switching nodes. Figure 1 shows a network with 8 processor nodes, which means there are 32 switching nodes. It also represents each node as N(rank, column number). For example, node at column 6 in rank 1 is represented as (1,6) and node at column 2 in rank 0 is represented as (0,2).
For any 'i' greater than zero, a switching node N(i,j) gets connected to N(i-1, j) and N(i-1, m), where 'm' is obtained by flipping the ith most significant bit of j. For example, consider the node N(1,6): i equals 1 and j equals 6, therefore m is obtained by flipping the first most significant bit of 6.
| Variable | Binary representation | Decimal Representation |
| j | 110 | 6 |
| m | 010 | 2 |
As a result the nodes connected to N(1,6) are :-
| N(i,j) | N(i-1,j) | N(i-1,m) |
| (1,6) | (0,6) | (0,2) |
Thus, N(0,6), N(1,6), N(0,2), N(1,2) form a butterfly pattern. Several butterfly patterns exist in the figure and therefore, this network is called Butterfly Network.
Butterfly network routing[3]
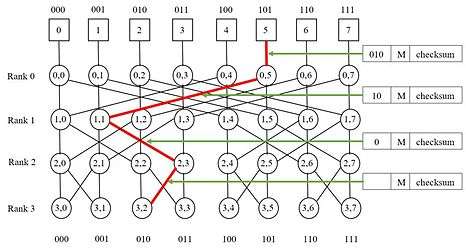
In a wrapped butterfly network (which means rank 0 gets merged with rank 3. In figure 2, it is shown by replicating the processor nodes below rank 3), a message is sent from processor 5 to processor 2. The packet transmitted over the link is of the form:
| Header | Payload | Trailer |
The header contains the destination of the message, which is processor 2 (010 in binary). The payload is the message 'M' and trailer contains checksum. Therefore the actual message transmitted from processor 5 is:
| 010 | M | checksum |
Upon reaching a switching node, one of the two output links is selected based on the most significant bit of the destination address. If that bit is zero, the left link is selected. If that bit is one, the right link is selected. Subsequently, this bit is removed from the destination address in the packet transmitted through the selected link. This is shown in figure 2.
- The above packet reaches N(0,5). From the header of the packet it removes the leftmost bit to decide the direction. Since it is a zero, left link of N(0,5) (which connects to N(1,1)) gets selected. The new header is '10'.
- The new packet reaches N(1,1). From the header of the packet it removes the leftmost bit to decide the direction. Since it is a one, right link of N(1,1) (which connects to N(2,3)) gets selected. The new header is '0'.
- The new packet reaches N(2,3). From the header of the packet it removes the leftmost bit to decide the direction. Since it is a zero, left link of N(2,3) (which connects to N(3,2)) gets selected. The header field is empty.
- Processor 2 receives the packet, which now contains only the payload 'M' and the checksum.
Butterfly network parameters[6]
There are several parameters to evaluate a network topology, but the prominent ones relevant in designing large scale multi-processor systems are discussed here. These parameters are summarized below and an explanation of how they are calculated for a butterfly network with 8 processor nodes as shown in figure 1 is provided.
- Bisection Bandwidth: A representative measure of the bandwidth bottleneck which restricts overall communication. It is the maximum bandwidth required to sustain communication between all nodes in the network. This can be interpreted as the minimum number of links that need to be severed to split the system into two equal portions. For example, the 8 node butterfly network can be split into two by cutting 4 links that crisscross across the middle. Thus bisection bandwidth of this particular system is 4.
- Diameter: This is the worst case latency (between two nodes) possible in the system. It can be calculated in terms of network hops, which is the number of links a message must travel in order to reach the destination node. In the 8 node butterfly network, it appears that N(0,0) and N(3,7) are farthest away, but upon inspecting carefully, it is apparent that due to the symmetric nature of the network, traversing from any rank 0 node to any rank 3 node requires only 3 hops. Therefore the diameter of this system is 3.
- Links: Total number of links required to construct the entire network structure. This is an indicator for overall cost and complexity of implementation. The example network shown in figure 1 requires a total of 48 links (16 links each between rank 0 and 1, rank 1 and 2, rank 2 and 3).
- Degree: Represents the complexity of each router in the network. This is equal to the number of in/out links connected to each switching node. The butterfly network switching nodes have 2 input links and 2 output links, hence it is a 4-degree network.
Comparison with other network topologies
This section compares the butterfly network with other network topologies like linear array, ring, 2-D mesh and hypercube.[7] Note that linear array can be considered as a 1-D mesh topology. All their relevant parameters are compiled in the below table[8] (‘p’ represents the number of processor nodes).
| Topology | Diameter | Bisection Bandwidth | Links | Degree |
| Linear array | p-1 | 1 | p-1 | 2 |
| Ring | p/2 | 2 | p | 2 |
| 2-D mesh | 2((√p) - 1) | √p | 2√p((√p) - 1) | 4 |
| Hypercube | log2(p) | p/2 | log2(p) × (p/2) | log2(p) |
| Butterfly | log2(p) | p/2 | log2(p) × 2p | 4 |
Advantages
- Butterfly networks have lower diameter than other toplogies like linear array,ring and 2-D mesh. This implies that in butterfly network, a message sent from one processor would reach its destination in lower number of network hops.
- Butterfly networks have higher bisection bandwidth than other toplogies like linear array,ring and 2-D mesh. This implies that in butterfly network, higher number of links need to be broken in order to prevent global communication.
Disadvantages
- Butterfly networks are more complex and costlier than other topologies like linear array, ring and 2-D mesh due to higher number of links required to sustain the network.
The difference between hypercube and butterfly lies within their implementation. Butterfly network has a symmetric structure where all processor nodes between two ranks are equidistant to each other, whereas hypercube is more suitable for a multi-processor system which demands unequal distances between its nodes. By looking at the number of links required, it may appear that hypercube is cheaper and simpler compared to a butterfly network, but as the number of processor nodes go beyond 16, the router cost and complexity (represented by degree) of butterfly network becomes lower than hypercube because its degree is independent of the number of nodes.
In conclusion, there is no single network topology which is best for all scenarios. The decision has to be made based on factors like number of processor nodes in the system, bandwidth-latency requirements, cost and scalability.
See also
References
- ↑ Solihin, Yan (2016). Fundamentals of Parallel Computer Architecture. Solihin Books. pp. 371–372. ISBN 978-0-9841630-0-7.
- ↑ Solihin, Yan (2016). Fundamentals of Parallel Computer Architecture. Solihin Books. pp. 373–374. ISBN 978-0-9841630-0-7.
- 1 2 3 4 Leighton, F.Thomson (1992). Introduction to Parallel Algorithms and Architectures: Arrays, Trees, Hypercubes. Morgan Kaufmann Publishers. ISBN 1-55860-117-1.
- ↑ T., LeBlanc,; M., Scott,; C., Brown, (1988-01-01). "Large-Scale Parallel Programming: Experience with the BBN Butterfly Parallel Processor".
- ↑ Jadhav, Sunitha S. Advanced Computer Architecture and Computing. Technical Publications. pp. Section 3–22. ISBN 9788184315721.
- ↑ Solihin, Yan (2016). Fundamentals of Parallel Computer Architecture. Solihin Books. pp. 377–378. ISBN 978-0-9841630-0-7.
- ↑ M. Arjomand, H. Sarbazi-Azad, "Performance Evaluation of Butterfly on-Chip Network for MPSoCs", International SoC Design Conference, pp. 1–296-1-299, 2008
- ↑ Solihin, Yan (2016). Fundamentals of Parallel Computer Architecture. Solihin Books. pp. 379–380. ISBN 978-0-9841630-0-7.