Branch predictor
In computer architecture, a branch predictor[1][2][3][4][5] is a digital circuit that tries to guess which way a branch (e.g. an if-then-else structure) will go before this is known for sure. The purpose of the branch predictor is to improve the flow in the instruction pipeline. Branch predictors play a critical role in achieving high effective performance in many modern pipelined microprocessor architectures such as x86.

Two-way branching is usually implemented with a conditional jump instruction. A conditional jump can either be "not taken" and continue execution with the first branch of code which follows immediately after the conditional jump, or it can be "taken" and jump to a different place in program memory where the second branch of code is stored. It is not known for certain whether a conditional jump will be taken or not taken until the condition has been calculated and the conditional jump has passed the execution stage in the instruction pipeline (see fig. 1).
Without branch prediction, the processor would have to wait until the conditional jump instruction has passed the execute stage before the next instruction can enter the fetch stage in the pipeline. The branch predictor attempts to avoid this waste of time by trying to guess whether the conditional jump is most likely to be taken or not taken. The branch that is guessed to be the most likely is then fetched and speculatively executed. If it is later detected that the guess was wrong then the speculatively executed or partially executed instructions are discarded and the pipeline starts over with the correct branch, incurring a delay.
The time that is wasted in case of a branch misprediction is equal to the number of stages in the pipeline from the fetch stage to the execute stage. Modern microprocessors tend to have quite long pipelines so that the misprediction delay is between 10 and 20 clock cycles. As a result, making a pipeline longer increases the need for a more advanced branch predictor.
The first time a conditional jump instruction is encountered, there is not much information to base a prediction on. But the branch predictor keeps records of whether branches are taken or not taken. When it encounters a conditional jump that has been seen several times before then it can base the prediction on the history. The branch predictor may, for example, recognize that the conditional jump is taken more often than not, or that it is taken every second time.
Branch prediction is not the same as branch target prediction. Branch prediction attempts to guess whether a conditional jump will be taken or not. Branch target prediction attempts to guess the target of a taken conditional or unconditional jump before it is computed by decoding and executing the instruction itself. Branch prediction and branch target prediction are often combined into the same circuitry.
Implementation
Static branch prediction
Static prediction is the simplest branch prediction technique because it does not rely on information about the dynamic history of code executing. Instead it predicts the outcome of a branch based solely on the branch instruction.[6]
The early implementations of SPARC and MIPS (two of the first commercial RISC architectures) use single-direction static branch prediction: they always predict that a conditional jump will not be taken, so they always fetch the next sequential instruction. Only when the branch or jump is evaluated and found to be taken, does the instruction pointer get set to a non-sequential address.
Both CPUs evaluate branches in the decode stage and have a single cycle instruction fetch. As a result, the branch target recurrence is two cycles long, and the machine always fetches the instruction immediately after any taken branch. Both architectures define branch delay slots in order to utilize these fetched instructions.
A more advanced form of static prediction presumes that backward branches will be taken and that forward branches will not. A backward branch is one that has a target address that is lower than its own address. This technique can help with prediction accuracy of loops, which are usually backward-pointing branches, and are taken more often than not taken.
Some processors allow branch prediction hints to be inserted into the code to tell whether the static prediction should be taken or not taken. The Intel Pentium 4 accepts branch prediction hints while this feature is abandoned in later processors.[7]
Static prediction is used as a fall-back technique in some processors with dynamic branch prediction when there isn't any information for dynamic predictors to use. Both the Motorola MPC7450 (G4e) and the Intel Pentium 4 use this technique as a fall-back.[8]
In static prediction, all decisions are made at compile time, before the execution of the program.[9]
Dynamic branch prediction
Dynamic branch prediction[2] uses information about taken or not taken branches gathered at run-time to predict the outcome of a branch.[1]
Next line prediction
Some superscalar processors (MIPS R8000, Alpha 21264 and Alpha 21464 (EV8)) fetch each line of instructions with a pointer to the next line. This next line predictor handles branch target prediction as well as branch direction prediction.
When a next line predictor points to aligned groups of 2, 4 or 8 instructions, the branch target will usually not be the first instruction fetched, and so the initial instructions fetched are wasted. Assuming for simplicity a uniform distribution of branch targets, 0.5, 1.5, and 3.5 instructions fetched are discarded, respectively.
Since the branch itself will generally not be the last instruction in an aligned group, instructions after the taken branch (or its delay slot) will be discarded. Once again assuming a uniform distribution of branch instruction placements, 0.5, 1.5, and 3.5 instructions fetched are discarded.
The discarded instructions at the branch and destination lines add up to nearly a complete fetch cycle, even for a single-cycle next-line predictor.
One-level branch prediction
Saturating counter
A 1-bit saturating counter records the last outcome of the branch. This is the most simple version possible, though not very effective.
A 2-bit saturating counter is a state machine with four states:
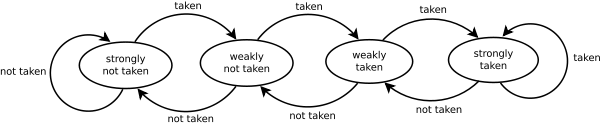
- Strongly not taken
- Weakly not taken
- Weakly taken
- Strongly taken
When a branch is evaluated, the corresponding state machine is updated. Branches evaluated as not taken decrement the state toward strongly not taken, and branches evaluated as taken increment the state toward strongly taken. The advantage of the two-bit counter over a one-bit scheme is that a conditional jump has to deviate twice from what it has done most in the past before the prediction changes. For example, a loop-closing conditional jump is mispredicted once rather than twice.
The original, non-MMX Intel Pentium processor uses a saturating counter, though with an imperfect implementation.[7]
On the SPEC'89 benchmarks, very large bimodal predictors saturate at 93.5% correct, once every branch maps to a unique counter.[10]
The predictor table is indexed with the instruction address bits, so that the processor can fetch a prediction for every instruction before the instruction is decoded.
Two-level predictor
The Two-Level Branch Predictor, also referred to as Correlation-Based Branch Predictor, uses a two-dimensional table of counters, also called "Pattern History Table". The table entries are two-bit counters.
Two-level adaptive predictor
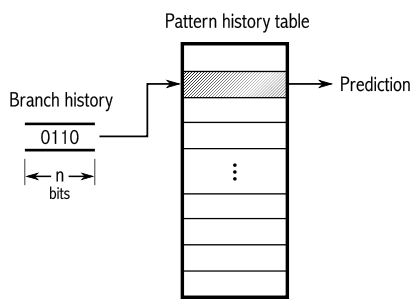
If an if statement is executed three times, the decision made on the third execution might depend upon whether the previous two were taken or not. In such scenarios, two-level adaptive predictor works more efficiently than a saturation counter. Conditional jumps that are taken every second time or have some other regularly recurring pattern are not predicted well by the saturating counter. A two-level adaptive predictor remembers the history of the last n occurrences of the branch and uses one saturating counter for each of the possible 2n history patterns. This method is illustrated in figure 3.
Consider the example of n = 2. This means that the last two occurrences of the branch are stored in a two-bit shift register. This branch history register can have four different binary values, 00, 01, 10 and 11, where zero means "not taken" and one means "taken". A pattern history table contains four entries per branch, one for each of the 22 = 4 possible branch histories, and each entry in the table contains a two-bit saturating counter of the same type as in figure 2 for each branch. The branch history register is used for choosing which of the four saturating counters to use. If the history is 00, then the first counter is used; if the history is 11, then the last of the four counters is used.
Assume, for example, that a conditional jump is taken every third time. The branch sequence is 001001001... In this case, entry number 00 in the pattern history table will go to state "strongly taken", indicating that after two zeroes comes a one. Entry number 01 will go to state "strongly not taken", indicating that after 01 comes a zero. The same is the case with entry number 10, while entry number 11 is never used because there are never two consecutive ones.
The general rule for a two-level adaptive predictor with an n-bit history is that it can predict any repetitive sequence with any period if all n-bit sub-sequences are different.[7]
The advantage of the two-level adaptive predictor is that it can quickly learn to predict an arbitrary repetitive pattern. This method was invented by T.-Y. Yeh and Yale Patt at the University of Michigan.[12] Since the initial publication in 1991, this method has become very popular. Variants of this prediction method are used in most modern microprocessors.
Local branch prediction
A local branch predictor has a separate history buffer for each conditional jump instruction. It may use a two-level adaptive predictor. The history buffer is separate for each conditional jump instruction, while the pattern history table may be separate as well or it may be shared between all conditional jumps.
The Intel Pentium MMX, Pentium II and Pentium III have local branch predictors with a local 4-bit history and a local pattern history table with 16 entries for each conditional jump.
On the SPEC'89 benchmarks, very large local predictors saturate at 97.1% correct.[13]
Global branch prediction
A global branch predictor does not keep a separate history record for each conditional jump. Instead it keeps a shared history of all conditional jumps. The advantage of a shared history is that any correlation between different conditional jumps is part of making the predictions. The disadvantage is that the history is diluted by irrelevant information if the different conditional jumps are uncorrelated, and that the history buffer may not include any bits from the same branch if there are many other branches in between. It may use a two-level adaptive predictor.
This scheme is only better than the saturating counter scheme for large table sizes, and it is rarely as good as local prediction. The history buffer must be longer in order to make a good prediction. The size of the pattern history table grows exponentially with the size of the history buffer. Hence, the big pattern history table must be shared among all conditional jumps.
A two-level adaptive predictor with globally shared history buffer and pattern history table is called a "gshare" predictor if it xors the global history and branch PC, and "gselect" if it concatenates them. Global branch prediction is used in AMD processors, and in Intel Pentium M, Core, Core 2, and Silvermont-based Atom processors.[14]
Alloyed branch prediction
An alloyed branch predictor[15] combines the local and global prediction principles by concatenating local and global branch histories, possibly with some bits from the program counter as well. Tests indicate that the VIA Nano processor may be using this technique.[7]
Agree predictor
An agree predictor is a two-level adaptive predictor with globally shared history buffer and pattern history table, and an additional local saturating counter. The outputs of the local and the global predictors are XORed with each other to give the final prediction. The purpose is to reduce contentions in the pattern history table where two branches with opposite prediction happen to share the same entry in the pattern history table.[16]
The agree predictor was used in the first version of the Intel Pentium 4, but was later abandoned.
Hybrid predictor
A hybrid predictor, also called combined predictor, implements more than one prediction mechanism. The final prediction is based either on a meta-predictor that remembers which of the predictors has made the best predictions in the past, or a majority vote function based on an odd number of different predictors.
Scott McFarling proposed combined branch prediction in his 1993 paper.[17]
On the SPEC'89 benchmarks, such a predictor is about as good as the local predictor.
Predictors like gshare use multiple table entries to track the behavior of any particular branch. This multiplication of entries makes it much more likely that two branches will map to the same table entry (a situation called aliasing), which in turn makes it much more likely that prediction accuracy will suffer for those branches. Once you have multiple predictors, it is beneficial to arrange that each predictor will have different aliasing patterns, so that it is more likely that at least one predictor will have no aliasing. Combined predictors with different indexing functions for the different predictors are called gskew predictors, and are analogous to skewed associative caches used for data and instruction caching.
Loop predictor
A conditional jump that controls a loop is best predicted with a special loop predictor. A conditional jump in the bottom of a loop that repeats N times will be taken N-1 times and then not taken once. If the conditional jump is placed at the top of the loop, it will be not taken N-1 times and then taken once. A conditional jump that goes many times one way and then the other way once is detected as having loop behavior. Such a conditional jump can be predicted easily with a simple counter. A loop predictor is part of a hybrid predictor where a meta-predictor detects whether the conditional jump has loop behavior.
Many microprocessors today have loop predictors.[7]
Indirect branch predictor
An indirect jump instruction can choose among more than two branches. Some processors have specialized indirect branch predictors.[18][19] Newer processors from Intel[20] and AMD[21] can predict indirect branches by using a two-level adaptive predictor. This kind of instruction contributes more than one bit to the history buffer. The zBC12 and later z/Architecture processors from IBM support a BRANCH PREDICTION PRELOAD instruction that can preload the branch predictor entry for a given instruction with a branch target address constructed by adding the contents of a general-purpose register to an immediate displacement value.[22][23]
Processors without this mechanism will simply predict an indirect jump to go to the same target as it did last time.[7]
Prediction of function returns
A function will normally return to where it is called from. The return instruction is an indirect jump that reads its target address from the call stack. Many microprocessors have a separate prediction mechanism for return instructions. This mechanism is based on a so-called return stack buffer, which is a local mirror of the call stack. The size of the return stack buffer is typically 4 - 16 entries.[7]
Overriding branch prediction
The trade-off between fast branch prediction and good branch prediction is sometimes dealt with by having two branch predictors. The first branch predictor is fast and simple. The second branch predictor, which is slower, more complicated, and with bigger tables, will override a possibly wrong prediction made by the first predictor.
The Alpha 21264 and Alpha EV8 microprocessors used a fast single-cycle next line predictor to handle the branch target recurrence and provide a simple and fast branch prediction. Because the next line predictor is so inaccurate, and the branch resolution recurrence takes so long, both cores have two-cycle secondary branch predictors which can override the prediction of the next line predictor at the cost of a single lost fetch cycle.
The Intel Core i7 has two branch target buffers and possibly two or more branch predictors.[24]
Neural branch prediction
Machine learning for branch prediction using LVQ and multi-layer perceptrons, called "neural branch prediction", was proposed by Prof. Lucian Vintan (Lucian Blaga University of Sibiu).[25] The neural branch predictor research was developed much further by Prof. Daniel Jimenez (Rutgers University, USA). In 2001, (HPCA Conference) the first perceptron predictor was presented that was feasible to implement in hardware. The first commercial implementation of perceptron branch predictor was in AMD's Piledriver microarchitecture.[26]
The main advantage of the neural predictor is its ability to exploit long histories while requiring only linear resource growth. Classical predictors require exponential resource growth. Jimenez reports a global improvement of 5.7% over a McFarling-style hybrid predictor.[27] He also used a gshare/perceptron overriding hybrid predictors.
The main disadvantage of the perceptron predictor is its high latency. Even after taking advantage of high-speed arithmetic tricks, the computation latency is relatively high compared to the clock period of many modern microarchitectures. In order to reduce the prediction latency, Jimenez proposed in 2003 the fast-path neural predictor, where the perceptron predictor chooses its weights according to the current branch’s path, rather than according to the branch’s PC. Many other researchers developed this concept (A. Seznec, M. Monchiero, D. Tarjan & K. Skadron, V. Desmet, Akkary et al., K. Aasaraai, Michael Black, etc.)
Most of the state-of-the-art branch predictors are using a perceptron predictor (see Intel's "Championship Branch Prediction Competition" [28]). Intel already implements this idea in one of the IA-64's simulators (2003).
The AMD Ryzen processor, previewed on December, 13th, 2016, revealed its newest processor architecture using a neural network based branch predictor to minimize prediction errors.[29][30]
History
The IBM Stretch, designed in the late 1950s, pre-executes all unconditional branches and any conditional branches that depended on the index registers. For other conditional branches, the first two production models implemented predict untaken; subsequent models were changed to implement predictions based on the current values of the indicator bits (corresponding to today's condition codes).[31] The Stretch designers had considered static hint bits in the branch instructions early in the project but decided against them. Misprediction recovery was provided by the lookahead unit on Stretch, and part of Stretch's reputation for less-than-stellar performance was blamed on the time required for misprediction recovery. Subsequent IBM large computer designs did not use branch prediction with speculative execution until the IBM 3090 in 1985.
Two-bit predictors were introduced by Tom McWilliams and Curt Widdoes in 1977 for the Lawrence Livermore National Lab S-1 supercomputer and independently by Jim Smith in 1979 at CDC.[32]
Microprogrammed processors, popular from the 1960s to the 1980s and beyond, took multiple cycles per instruction, and generally did not require branch prediction. However, in addition to the IBM 3090, there are several other examples of microprogrammed designs that incorporated branch prediction.
The Burroughs B4900, a microprogrammed COBOL machine released around 1982, was pipelined and used branch prediction. The B4900 branch prediction history state is stored back into the in-memory instructions during program execution. The B4900 implements 4-state branch prediction by using 4 semantically equivalent branch opcodes to represent each branch operator type. The opcode used indicated the history of that particular branch instruction. If the hardware determines that the branch prediction state of a particular branch needs to be updated, it rewrites the opcode with the semantically equivalent opcode that hinted the proper history. This scheme obtains a 93% hit rate. US patent 4,435,756 and others were granted on this scheme.
The VAX 9000, announced in 1989, is both microprogrammed and pipelined, and performs branch prediction.[33]
The first commercial RISC processors, the MIPS R2000 and R3000 and the earlier SPARC processors, do only trivial "not-taken" branch prediction. Because they use branch delay slots, fetched just one instruction per cycle, and execute in-order, there is no performance loss. The later, R4000 uses the same trivial "not-taken" branch prediction, and loses two cycles to each taken branch because the branch resolution recurrence is four cycles long.
Branch prediction became more important with the introduction of pipelined superscalar processors like the Intel Pentium, DEC Alpha 21064, the MIPS R8000, and the IBM POWER series. These processors all rely on one-bit or simple bimodal predictors.
The DEC Alpha 21264 (EV6) uses a next-line predictor overridden by a combined local predictor and global predictor, where the combining choice is made by a bimodal predictor.[34]
The AMD K8 has a combined bimodal and global predictor, where the combining choice is another bimodal predictor. This processor caches the base and choice bimodal predictor counters in bits of the L2 cache otherwise used for ECC. As a result, it has effectively very large base and choice predictor tables, and parity rather than ECC on instructions in the L2 cache. Parity is just fine, since any instruction suffering a parity error can be invalidated and refetched from memory.
The Alpha 21464[34] (EV8, cancelled late in design) had a minimum branch misprediction penalty of 14 cycles. It was to use a complex but fast next line predictor overridden by a combined bimodal and majority-voting predictor. The majority vote was between the bimodal and two gskew predictors.
See also
- Branch target predictor
- Branch predication
- Branch prediction analysis attacks – on RSA public-key cryptography
- Instruction unit
- Instruction prefetch
- Cache prefetching
References
- 1 2 Alexey Malishevsky; Douglas Beck; Andreas Schmid; Eric Landry. "Dynamic Branch Prediction".
- 1 2 Chih-Cheng Cheng. "The Schemes and Performances of Dynamic Branch predictors" (PDF).
- ↑ Raj Parihar. "Branch Prediction Techniques and Optimizations" (PDF).
- ↑ Onur Mutlu (February 11, 2013). "18-447 Computer Architecture Lecture 11: Branch Prediction" (PDF).
- ↑ Pierre Michaud; André Seznec; Richard Uhlig (September 1996). "Skewed branch predictors" (PDF).
- ↑ P. Shen, John; Lipasti, Mikko (2005). Modern processor design: fundamentals of superscalar processors. Boston: McGraw-Hill Higher Education. p. 455. ISBN 0-07-057064-7.
- 1 2 3 4 5 6 7 Fog, Agner (2016-12-01). "The microarchitecture of Intel, AMD and VIA CPUs" (PDF). p. 36. Retrieved 2017-03-22.
- ↑ The Pentium 4 and the G4e: an Architectural Comparison, Ars Technica
- ↑ Jim Plusquellic. "CMSC 611: Advanced Computer Architecture, Chapter 4 (Part V)".
- ↑ S. McFarling Combining Branch Predictors Digital Western Research Lab (WRL) Technical Report, TN-36, 1993
- ↑ "New Algorithm Improves Branch Prediction: 3/27/95" (PDF). Carnegie Mellon University. Retrieved February 2, 2016.
- ↑ Yeh, T.-Y.; Patt, Y. N. (1991). "Two-Level Adaptive Training Branch Prediction". Proceedings of the 24th annual international symposium on Microarchitecture. Albuquerque, New Mexico, Puerto Rico: ACM. pp. 51–61.
- ↑ S. McFarling Combining Branch Predictors Digital Western Research Lab (WRL) Technical Report, TN-36, 1993:8
- ↑ "Silvermont, Intel’s Low Power Architecture (page 2)". Real World Technologies.
- ↑ Skadron, K.; Martonosi, M; Clark, D.W. (Oct 2000). "A Taxonomy of Branch Mispredictions, and Alloyed Prediction as a Robust Solution to Wrong-History Mispredictions". Proceedings of the 2000 International Conference on Parallel Architectures and Compilation Techniques. Philadelphia.
- ↑ Sprangle, E.; et al. (June 1997). "The Agree Predictor: A Mechanism for Reducing Negative Branch History Interference". Proceedings of the 24th International Symposium on Computer Architecture. Denver.
- ↑ McFarling (1993). "Combining Branch Predictors" — introduces combined predictors.
- ↑ "Cortex-A15 MPCore Technical Reference Manual, section 6.5.3 "Indirect predictor"". ARM Holdings.
- ↑ Karel Driesen; Urs Hölzle (June 25, 1997). "Limits of Indirect Branch Prediction" (PDF).
- ↑ Jon Stokes (February 25, 2004). "A Look at Centrino’s Core: The Pentium M". pp. 2–3.
- ↑ Aaron Kanter (October 28, 2008). "Performance Analysis for Core 2 and K8: Part 1". p. 5.
- ↑ "z/Architecture Principles of Operation" (PDF). IBM. March 2015. pp. 7–40 – 7–43. SA22-7832-10.
- ↑ "IBM zEnterprise BC12 Technical Guide" (PDF). IBM. February 2014. p. 78.
- ↑ WO 2000/014628, Yeh, Tse-Yu & H P Sharangpani, "A method and apparatus for branch prediction using a second level branch prediction table", published 16.03.2000
- ↑ Lucian N. Vintan (1999). Towards a High Performance Neural Branch Predictor (PDF). Proc. Int'l J. Conf. on Neural Networks (IJCNN).
- ↑ Jarred Walton (May 15, 2012). "The AMD Trinity Review (A10-4600M): A New Hope". AnandTech.
- ↑ Daniel A. Jimenez. "Fast Path-Based Neural Branch Prediction" (PDF). Retrieved March 18, 2016.
- ↑ "Championship Branch Prediction".
- ↑ "AMD Takes Computing to a New Horizon with Ryzen™ Processors". www.amd.com. Retrieved 2016-12-14.
- ↑ "AMD’s Zen CPU is now called Ryzen, and it might actually challenge Intel". Ars Technica UK. Retrieved 2016-12-14.
- ↑ IBM Stretch (7030) -- Aggressive Uniprocessor Parallelism
- ↑ S-1 Supercomputer
- ↑ Micro-architecture of the VAX 9000
- 1 2 Seznec, Felix, Krishnan, Sazeides. Design Tradeoffs for the Alpha EV8 Conditional Branch Predictor
External links
- Seznec et al. (1996). "Multiple-Block Ahead Branch Predictors" – demonstrates prediction accuracy is not impaired by indexing with previous branch address.
- Seznec et al. (2002). "Design Tradeoffs for the Alpha EV8 Conditional Branch Predictor" – describes the Alpha EV8 branch predictor. This paper does an excellent job discussing how they arrived at their design from various hardware constraints and simulation studies.
- Jimenez (2003). "Reconsidering Complex Branch Predictors" – describes the EV6 and K8 branch predictors, and pipelining considerations.
- Fog, Agner (2009). "The microarchitecture of Intel, AMD and VIA CPUs". Retrieved 2009-10-01.
- Andrews, Jeff (2007-10-30). "Branch and Loop Reorganization to Prevent Mispredicts". Intel Software Network. Retrieved 2008-08-20.
- Yee, Alexander. "What is Branch Prediction? - Stack Overflow Example".