Cupola (geometry)

Set of cupolae
Pentagonal cupola (example)
Schläfli symbol	{n} \|\| t{n}
Faces	n triangles, n squares, 1 n-gon, 1 2n-gon
Edges	5n
Vertices	3n
Symmetry group	C_nv, [1,n], (*nn), order 2n
Rotation group	C_n, [1,n]⁺, (nn), order n
Dual	Trapyramids
Properties	convex

In geometry, a cupola is a solid formed by joining two polygons, one (the base) with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

A cupola can be seen as a prism where one of the polygons has been collapsed in half by merging alternate vertices.

A cupola can be given an extended Schläfli symbol {n} || t{n}, representing a regular polygon {n} joined by a parallel of its truncation, t{n} or {2n}.

Cupolae are a subclass of the prismatoids.

Examples

Family of convex cupolae
n	2	3	4	5	6
Name	{2} \|\| t{2}	{3} \|\| t{3}	{4} \|\| t{4}	{5} \|\| t{5}	{6} \|\| t{6}
Cupola	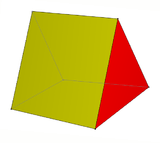Digonal cupola	Triangular cupola	Square cupola	Pentagonal cupola	Hexagonal cupola (Flat)
Related uniform polyhedra	Triangular prism	Cubocta- hedron	Rhombi- cubocta- hedron	Rhomb- icosidodeca- hedron	Rhombi- trihexagonal tiling

Plane "hexagonal cupolae" in the rhombitrihexagonal tiling

The above-mentioned three polyhedra are the only non-trivial convex cupolae with regular faces: The "hexagonal cupola" is a plane figure, and the triangular prism might be considered a "cupola" of degree 2 (the cupola of a line segment and a square). However, cupolae of higher-degree polygons may be constructed with irregular triangular and rectangular faces.

Coordinates of the vertices

A 40-sided cupola has 40 isosceles triangles (blue), 40 rectangles (yellow), a top regular 40-gon (red) and a bottom regular 80-gon (hidden).

The definition of the cupola does not require the base (or the side opposite the base, which can be called the top) to be a regular polygon, but it is convenient to consider the case where the cupola has its maximal symmetry, C_nv. In that case, the top is a regular n-gon, while the base is either a regular 2n-gon or a 2n-gon which has two different side lengths alternating and the same angles as a regular 2n-gon. It is convenient to fix the coordinate system so that the base lies in the xy-plane, with the top in a plane parallel to the xy-plane. The z-axis is the n-fold axis, and the mirror planes pass through the z-axis and bisect the sides of the base. They also either bisect the sides or the angles of the top polygon, or both. (If n is even, half of the mirror planes bisect the sides of the top polygon and half bisect the angles, while if n is odd, each mirror plane bisects one side and one angle of the top polygon.) The vertices of the base can be designated V₁ through V_2n, while the vertices of the top polygon can be designated V_2n+1 through V_3n. With these conventions, the coordinates of the vertices can be written as:

V_2j−1: (r_b cos[2π(j − 1) / n + α], r_b sin[2π(j − 1) / n + α], 0)
V_2j: (r_b cos(2πj / n − α), r_b sin(2πj / n − α), 0)
V_2n+j: (r_t cos(πj / n), r_t sin(πj / n), h)

where j = 1, 2, ..., n.

Since the polygons V₁V₂V_2n+2V_2n+1, etc. are rectangles, this puts a constraint on the values of r_b, r_t, and α. The distance V₁V₂ is equal to

r_b{[cos(2π / n − α) − cos α]² + [sin(2π / n − α) − sin α]²}^¹⁄₂

= r_b{[cos²(2π / n − α) − 2cos(2π / n − α)cos α + cos² α] + [sin²(2π / n − α) − 2sin(2π / n − α)sin α + sin² α]}^¹⁄₂

= r_b{2[1 − cos(2π / n − α)cos α − sin(2π / n − α)sin α]}^¹⁄₂

= r_b{2[1 − cos(2π / n − 2α)]}^¹⁄₂

while the distance V_2n+1V_2n+2 is equal to

r_t{[cos(π / n) − 1]² + sin²(π / n)}^¹⁄₂

= r_t{[cos²(π / n) − 2cos(π / n) + 1] + sin²(π / n)}^¹⁄₂

= r_t{2[1 − cos(π / n)]}^¹⁄₂.

These are to be equal, and if this common edge is denoted by s,

r_b = s / {2[1 − cos(2π / n − 2α)]}^¹⁄₂

r_t = s / {2[1 − cos(π / n)]}^¹⁄₂

These values are to be inserted into the expressions for the coordinates of the vertices given earlier.

Star-cupolae

Family of star-cupolae
n / d	4	5	7	8
3	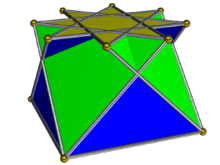{4/3}	{5/3}	{7/3}	{8/3}
5	—	—	{7/5}	{8/5}

Family of star-cuploids
n / d	3	5	7
2	Crossed triangular cuploid	Pentagrammic cuploid	Heptagrammic cuploid
4	—	Crossed pentagonal cuploid	Crossed heptagrammic cuploid

Star cupolae exist for all bases {n/d} where ⁶/₅ < ⁿ/_d < 6 and d is odd. At the limits the cupolae collapse into plane figures: beyond the limits the triangles and squares can no longer span the distance between the two polygons. When d is even, the bottom base {2n/d} becomes degenerate: we can form a cuploid or semicupola by withdrawing this degenerate face and instead letting the triangles and squares connect to each other here. In particular, the tetrahemihexahedron may be seen as a {3/2}-cuploid. The cupolae are all orientable, while the cuploids are all nonorientable. When n/d > 2 in a cuploid, the triangles and squares do not cover the entire base, and a small membrane is left in the base that simply covers empty space. Hence the {5/2} and {7/2} cuploids pictured above have membranes (not filled in), while the {5/4} and {7/4} cuploids pictured above do not.

The height h of an {n/d}-cupola or cuploid is given by the formula $h={\sqrt {1-{\frac {1}{4\sin ^{{2}}({\frac {\pi d}{n}})}}}}$ . In particular, h = 0 at the limits of n/d = 6 and n/d = 6/5, and h is maximized at n/d = 2 (the triangular prism, where the triangles are upright).^[1]^[2]

In the images above, the star cupolae have been given a consistent colour scheme to aid identifying their faces: the base n/d-gon is red, the base 2n/d-gon is yellow, the squares are blue, and the triangles are green. The cuploids have the base n/d-gon red, the squares yellow, and the triangles blue, as the other base has been withdrawn.

Anticupola

Set of anticupolas
Pentagonal example
Schläfli symbol	s{n} \|\| t{n}
Faces	3n triangles 1 n-gon, 1 2n-gon
Edges	6n
Vertices	3n
Symmetry group	C_nv, [1,n], (*nn), order 2n
Rotation group	C_n, [1,n]⁺, (nn), order n
Dual	?
Properties	convex

An n-gonal anticupola is constructed from a regular 2n-gonal base, 3n triangles as two types, and a regular n-gonal top. For n=2, the top digon face is reduced to a single edge. The vertices of the top polygon are aligned with vertices in the lower polygon. The symmetry is C_nv, order 2n.

An anticupola can't be constructed with all regular faces, although some can be made regular. If the top n-gon and triangles are regular, the base 2n-gon can not be planar and regular. In such a case, n=6 generates a regular hexagon and surrounding equilateral triangles of a snub hexagonal tiling, which can be closed into a zero volume polygon with the base a symmetric 12-gon shaped like a larger hexagon, having adjacent pairs of colinear edges.

Two anticupola can be augmented together on their base as a bianticupolae.

Family of convex anticupolae
n	2	3	4	5	6...
Name	s{2} \|\| t{2}	s{3} \|\| t{3}	s{4} \|\| t{4}	s{5} \|\| t{5}	s{6} \|\| t{6}
Image	Digonal	Triangular	Square	Pentagonal	Hexagonal
Transparent
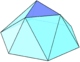Net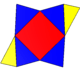

Hypercupolae

The hypercupolae or polyhedral cupolae are a family of convex nonuniform polychora (here four-dimensional figures), analogous to the cupolas. Each one's bases are a Platonic solid and its expansion.^[3]

Name	Tetrahedral cupola		Cubic cupola		Octahedral cupola		Dodecahedral cupola		Hexagonal tiling cupola
Schläfli symbol	{3,3} \|\| rr{3,3}		{4,3} \|\| rr{4,3}		{3,4} \|\| rr{3,4}		{5,3} \|\| rr{5,3}		{6,3} \|\| rr{6,3}
Segmentochora index^[3]	K4.23		K4.71		K4.107		K4.152
circumradius	1		sqrt((3+sqrt(2))/2) = 1.485634		sqrt(2+sqrt(2)) = 1.847759		3+sqrt(5) = 5.236068
Image
Cap cells
Vertices	16		32		30		80		∞
Edges	42		84		84		210		∞
Faces	42	24 {3} + 18 {4}	80	32 {3} + 48 {4}	82	40 {3} + 42 {4}	194	80 {3} + 90 {4} + 24 {5}	∞
Cells	16	1 tetrahedron 4 triangular prisms 6 triangular prisms 4 triangular pyramids 1 cuboctahedron	28	1 cube 6 square prisms 12 triangular prisms 8 triangular pyramids 1 rhombicuboctahedron	28	1 octahedron 8 triangular prisms 12 triangular prisms 6 square pyramids 1 rhombicuboctahedron	64	1 dodecahedron 12 pentagonal prisms 30 triangular prisms 20 triangular pyramids 1 rhombicosidodecahedron	∞	1 hexagonal tiling ∞ hexagonal prisms ∞ triangular prisms ∞ triangular pyramids 1 rhombitrihexagonal tiling
Related uniform polychora	runcinated 5-cell		runcinated tesseract		runcinated 24-cell		runcinated 120-cell		runcinated hexagonal tiling honeycomb

References

↑ http://www.orchidpalms.com/polyhedra/cupolas/cupola1.html
↑ http://www.orchidpalms.com/polyhedra/cupolas/cupola2.html
1 2 Convex Segmentochora Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1-4, 139-181, 2000

Johnson, N.W. Convex Polyhedra with Regular Faces. Canad. J. Math. 18, 169–200, 1966.

External links

Weisstein, Eric Wolfgang. "Cupola". MathWorld.

Segmentotopes

Convex polyhedra

Platonic solids (regular)

Archimedean solids
(semiregular or uniform)

Catalan solids
(duals of Archimedean)

Dihedral regular

dihedron
hosohedron

Dihedral uniform

prisms antiprisms
duals:	bipyramids trapezohedra

Dihedral others

Degenerate polyhedra are in italics.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.