Absolutely convex set

A set C in a real or complex vector space is said to be absolutely convex or disked if it is convex and balanced (circled), in which case it is called a disk.

Properties

A set $C$ is absolutely convex if and only if for any points $x_{1},\,x_{2}$ in $C$ and any numbers $\lambda _{1},\,\lambda _{2}$ satisfying $|\lambda _{1}|+|\lambda _{2}|\leq 1$ the sum $\lambda _{1}x_{1}+\lambda _{2}x_{2}$ belongs to $C$ .

Since the intersection of any collection of absolutely convex sets is absolutely convex then for any subset A of a vector space one can define its absolutely convex hull to be the intersection of all absolutely convex sets containing A.

Absolutely convex hull

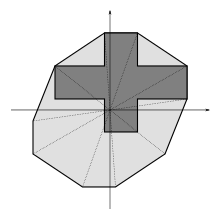
The light gray area is the Absolutely convex hull of the cross.

The absolutely convex hull of the set A is defined to be

${\mbox{absconv}}A=\left\{\sum _{{i=1}}^{n}\lambda _{i}x_{i}:n\in \mathbb{N} ,\,x_{i}\in A,\,\sum _{{i=1}}^{n}|\lambda _{i}|\leq 1\right\}$ .

References

Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics. 53. Cambridge University Press. pp. 4–6.
Narici, Lawrence; Beckenstein, Edward (July 26, 2010). Topological Vector Spaces, Second Edition. Pure and Applied Mathematics (Second ed.). Chapman and Hall/CRC.

Schaefer, H.H. (1999). Topological vector spaces. Springer-Verlag Press. p. 39.

Functional analysis (topics)
TVS types	Banach Banach Lattice Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert (pre-Hilbert) LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Strictly convex Webbed Topological tensor product (of Hilbert spaces)
Mapping topologies	Dual Dual space Operator Ultraweak Weak (operator) Mackey Strong (polar operator) Ultrastrong Uniform convergence
Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary
Operator theory	Banach algebras C-algebras Spectrum (C-algebra radius) Spectral theory (of ODEs Spectral theorem) Polar decomposition Singular value decomposition
Theorems	Banach–Alaoglu Banach–Mazur Banach–Saks Bessel's inequality Cauchy–Schwarz inequality Closed graph Closed range Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Gelfand–Naimark Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Krein–Milman Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point
Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure Weakly measurable function
Types of sets	Absolutely convex Absorbing Balanced Bounded Convex Convex cone (subset) Linear cone (subset) Radial Star-shaped Symmetric Zonotope
Subsets / set operations	Algebraic interior (core) Bounding points Convex hull Extreme point Interior Minkowski addition Polar

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

Absolutely convex set

Properties

Absolutely convex hull

See also

References