2

← 1 2 3 →
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]]
Cardinal two
Ordinal 2nd (second / twoth)
Numeral system binary
Factorization prime
Gaussian integer factorization
Prime 1st
Divisors 1, 2
Roman numeral II
Roman numeral (unicode) Ⅱ, ⅱ
Greek prefix di-
Latin prefix duo- bi-
Old English prefix twi-
Binary 102
Ternary 23
Quaternary 24
Quinary 25
Senary 26
Octal 28
Duodecimal 212
Hexadecimal 216
Vigesimal 220
Base 36 236
Greek numeral β'
Arabic & Kurdish ٢
Urdu ۲
Ge'ez ፪
Bengali ২
Chinese numeral 二，弍，贰，貳
Devanāgarī २ (do)
Telugu ౨
Tamil ௨
Hebrew ב (Bet)
Khmer ២
Korean 이，둘
Thai ๒

2 (Two; /ˈtuː/) is a number, numeral, and glyph. It is the natural number following 1 and preceding 3.

In mathematics

An integer is called even if it is divisible by 2. For integers written in a numeral system based on an even number, such as decimal and hexadecimal, divisibility by 2 is easily tested by merely looking at the last digit. If it is even, then the whole number is even. In particular, when written in the decimal system, all multiples of 2 will end in 0, 2, 4, 6, or 8.

Two is the smallest and first prime number, and the only even prime number (for this reason it is sometimes called "the oddest prime").[1] The next prime is three. Two and three are the only two consecutive prime numbers. 2 is the first Sophie Germain prime, the first factorial prime, the first Lucas prime, the first Ramanujan prime,[2] and the first Smarandache-Wellin prime.

Two is the third Fibonacci number.

Two is the base of the simplest numeral system in which natural numbers can be written concisely, being the length of the number a logarithm of the value of the number (whereas in base 1 the length of the number is the value of the number itself); the binary system is used in computers.

For any number x:

x + x = 2 · x addition to multiplication
x · x = x2 multiplication to exponentiation
xx = x↑↑2 exponentiation to tetration

In general:

hyper(x,n,x) = hyper(x,(n + 1),2)

Two also has the unique property that 2 + 2 = 2 · 2 = 22 = 2↑↑2 = 2↑↑↑2, and so on, no matter how high the level of the hyperoperation is.

Two is the only number x such that the sum of the reciprocals of the powers of x equals itself. In symbols

This comes from the fact that:

Powers of two are central to the concept of Mersenne primes, and important to computer science. Two is the first Mersenne prime exponent.

Taking the square root of a number is such a common mathematical operation, that the spot on the root sign where the exponent would normally be written for cubic roots and other such roots, is left blank for square roots, as it is considered tacit.

The square root of 2 was the first known irrational number.

The smallest field has two elements.

In the set-theoretical construction of the natural numbers, 2 is identified with the set {{∅},∅}. This latter set is important in category theory: it is a subobject classifier in the category of sets.

Two also has the unique property such that

and also

for a not equal to zero

In n-dimensional space for any n, any two distinct points determine a line.

For any polyhedron homeomorphic to a sphere, the Euler characteristic is χ = V − E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces.

List of basic calculations

Multiplication 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 50 100 1000
2 × x 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 100 200 2000
Division 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2 ÷ x 2 1 0.6 0.5 0.4 0.3 0.285714 0.25 0.2 0.2 0.18 0.16 0.153846 0.142857 0.13
x ÷ 2 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5
Exponentiation 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2x 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 32768 65536 131072 262144 524288 1048576
x2 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400

Evolution of the glyph

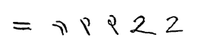
The glyph used in the modern Western world to represent the number 2 traces its roots back to the Brahmin Indians, who wrote "2" as two horizontal lines. The modern Chinese and Japanese languages still use this method. The Gupta rotated the two lines 45 degrees, making them diagonal, and sometimes also made the top line shorter and made its bottom end curve towards the center of the bottom line. Apparently for speed, the Nagari started making the top line more like a curve and connecting to the bottom line. The Ghubar Arabs made the bottom line completely vertical, and now the glyph looks like a dotless closing question mark. Restoring the bottom line to its original horizontal position, but keeping the top line as a curve that connects to the bottom line leads to our modern glyph.[3]

In fonts with text figures, 2 usually is of x-height, for example, .

In science

In technology

In religion

Judaism

The number 2 is important in Judaism, with one of the earliest references being that God ordered Noah to put two of every unclean animal (Gen. 7:2) in his ark (see Noah's Ark). Later on, the Ten Commandments were given in the form of two tablets. The number also has ceremonial importance, such as the two candles that are traditionally kindled to usher in the Shabbat, recalling the two different ways Shabbat is referred to in the two times the Ten Commandments are recorded in the Torah. These two expressions are known in Hebrew as שמור וזכור ("guard" and "remember"), as in "Guard the Shabbat day to sanctify it" (Deut. 5:12) and "Remember the Shabbat day to sanctify it" (Ex. 20:8). Two challahs (lechem mishneh) are placed on the table for each Shabbat meal and a blessing made over them, to commemorate the double portion of manna which fell in the desert every Friday to cover that day's meals and the Shabbat meals.

In Jewish law, the testimonies of two witnesses are required to verify and validate events, such as marriage, divorce, and a crime that warrants capital punishment.

"Second-Day Yom Tov" (Yom Tov Sheini Shebegaliyot) is a rabbinical enactment that mandates a two-day celebration for each of the one-day Jewish festivals (i.e., the first and seventh day of Passover, the day of Shavuot, the first day of Sukkot, and the day of Shemini Atzeret) outside the Land of Israel.

Numerological significance

The twos of all four suits in playing cards

The most common philosophical dichotomy is perhaps the one of good and evil, but there are many others. See dualism for an overview. In Hegelian dialectic, the process of synthesis creates two perspectives from one.

The ancient Sanskrit language of India, does not only have a singular and plural form for nouns, as do many other languages, but instead has, a singular (1) form, a dual (2) form, and a plural (everything above 2) form, for all nouns, due to the significance of 2. It is viewed as important because of the anatomical significance of 2 (2 hands, 2 nostrils, 2 eyes, 2 legs, etc.)

Two (二, èr) is a good number in Chinese culture. There is a Chinese saying, "good things come in pairs". It is common to use double symbols in product brand names, e.g. double happiness, double coin, double elephants etc. Cantonese people like the number two because it sounds the same as the word "easy" (易) in Cantonese.

In Finland, two candles are lit on Independence Day and put on a windowsill, to remind passersby of the sacrifices of past generations in the struggle for independence and democracy.[4]

In pre-1972 Indonesian and Malay orthography, 2 was shorthand for the reduplication that forms plurals: orang "person", orang-orang or orang2 "people".

In Astrology, Taurus is the second sign of the Zodiac.

In sports

In other fields

Groups of two:

In North American educational systems, the number 2.00 denotes a grade-point average of "C", which in some colleges and universities is the minimum required for good academic standing at the undergraduate level.[5]

See also

References

  1. ↑ John Horton Conway & Richard K. Guy, The Book of Numbers. New York: Springer (1996): 25. ISBN 0-387-97993-X. "Two is celebrated as the only even prime, which in some sense makes it the oddest prime of all."
  2. ↑ "Sloane's A104272 : Ramanujan primes". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
  3. ↑ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 393, Fig. 24.62
  4. ↑ UUSI-VIDENOJA, Hannu (6 December 1994). "Candles light nation's way: MESSAGE". South China Morning Post. Retrieved 9 May 2017.
  5. ↑ For a typical example, see the University of Oklahoma grading regulations.
Look up two or both in Wiktionary, the free dictionary.
Wikimedia Commons has media related to:
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.