Alpha helix

Protein secondary structure Beta sheet Alpha helix
The image above contains clickable links
Interactive diagram of hydrogen bonds in protein secondary structure. Cartoon above, atoms below with nitrogen in blue, oxygen in red (PDB: 1AXC​​)

The Alpha Helix (α-helix) is a common motif in the secondary structure of proteins and is a righthand-spiral conformation (i.e. helix) in which every backbone N−H group donates a hydrogen bond to the backbone C=O group of the amino acid located three or four residues earlier along the protein sequence.

Alpha Helix is also called a classic Pauling–Corey–Branson α-helix. The name 3.613-helix is also used for this type of helix, denoting the average number of residues per helical turn, with 13 atoms being involved in the ring formed by the hydrogen bond.

Among types of local structure in proteins, the α-helix is the most regular and the most predictable from sequence, as well as the most prevalent.

Discovery

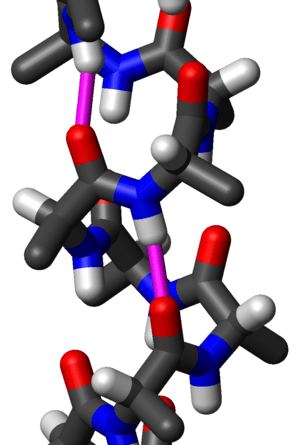
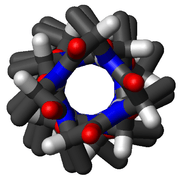
Side view of an α-helix of alanine residues in atomic detail. Two hydrogen bonds for the same peptide group are highlighted in magenta; the H to O distance is about 2 Å (0.20 nm). The protein chain runs upward here; that is, its N-terminus is at the bottom and its C-terminus at the top. Note that the sidechains (black stubs) angle slightly downward, toward the N-terminus, while the peptide oxygens (red) point up and the peptide NHs (blue with grey stubs) point down.
Top view of the same helix shown above. Four carbonyl groups are pointing upwards toward the viewer, spaced roughly 100° apart on the circle, corresponding to 3.6 amino-acid residues per turn of the helix.

In the early 1930s, William Astbury showed that there were drastic changes in the X-ray fiber diffraction of moist wool or hair fibers upon significant stretching. The data suggested that the unstretched fibers had a coiled molecular structure with a characteristic repeat of ~5.1 ångströms (0.51 nanometres).

Astbury initially proposed a kinked-chain structure for the fibers. He later joined other researchers (notably the American chemist Maurice Huggins) in proposing that:

Although incorrect in their details, Astbury's models of these forms were correct in essence and correspond to modern elements of secondary structure, the α-helix and the β-strand (Astbury's nomenclature was kept), which were developed by Linus Pauling, Robert Corey and Herman Branson in 1951 (see below); that paper showed both right- and left-handed helices, although in 1960 the crystal structure of myoglobin[1] showed that the right-handed form is the common one. Hans Neurath was the first to show that Astbury's models could not be correct in detail, because they involved clashes of atoms.[2] Neurath's paper and Astbury's data inspired H. S. Taylor,[3] Maurice Huggins[4] and Bragg and collaborators[5] to propose models of keratin that somewhat resemble the modern α-helix.

Two key developments in the modeling of the modern α-helix were: the correct bond geometry, thanks to the crystal structure determinations of amino acids and peptides and Pauling's prediction of planar peptide bonds; and his relinquishing of the assumption of an integral number of residues per turn of the helix. The pivotal moment came in the early spring of 1948, when Pauling caught a cold and went to bed. Being bored, he drew a polypeptide chain of roughly correct dimensions on a strip of paper and folded it into a helix, being careful to maintain the planar peptide bonds. After a few attempts, he produced a model with physically plausible hydrogen bonds. Pauling then worked with Corey and Branson to confirm his model before publication.[6] In 1954, Pauling was awarded his first Nobel Prize "for his research into the nature of the chemical bond and its application to the elucidation of the structure of complex substances" (such as proteins), prominently including the structure of the α-helix.

Structure

Geometry and hydrogen bonding

The amino acids in an α-helix are arranged in a right-handed helical structure where each amino acid residue corresponds to a 100° turn in the helix (i.e., the helix has 3.6 residues per turn), and a translation of 1.5 Å (0.15 nm) along the helical axis. Dunitz[7] describes how Pauling's first article on the theme in fact shows a left-handed helix, the enantiomer of the true structure. Short pieces of left-handed helix sometimes occur with a large content of achiral glycine amino acids, but are unfavorable for the other normal, biological L-amino acids. The pitch of the alpha-helix (the vertical distance between consecutive turns of the helix) is 5.4 Å (0.54 nm), which is the product of 1.5 and 3.6. What is most important is that the N-H group of an amino acid forms a hydrogen bond with the C=O group of the amino acid four residues earlier; this repeated i + 4 → i hydrogen bonding is the most prominent characteristic of an α-helix. Official international nomenclature[8] specifies two ways of defining α-helices, rule 6.2 in terms of repeating φ, ψ torsion angles (see below) and rule 6.3 in terms of the combined pattern of pitch and hydrogen bonding. The α-helices can be identified in protein structure using several computational methods, one of which being DSSP (Dictionary of Protein Secondary Structure).[9]

Contrast of helix end views between α (offset squarish) vs 310 (triangular)

Similar structures include the 310 helix (i + 3 → i hydrogen bonding) and the π-helix (i + 5 → i hydrogen bonding). The α-helix can be described as a 3.613 helix, since the i + 4 spacing adds three more atoms to the H-bonded loop compared to the tighter 310 helix, and on average, 3.6 amino acids are involved in one ring of α-helix. The subscripts refer to the number of atoms (including the hydrogen) in the closed loop formed by the hydrogen bond.[10]

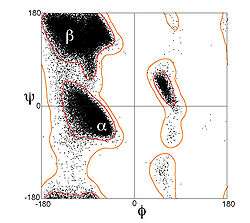
Ramachandran plot (φ, ψ plot), with data points for α-helical residues forming a dense diagonal cluster below and left of center, around the global energy minimum for backbone conformation.[11]

Residues in α-helices typically adopt backbone (φ, ψ) dihedral angles around (−60°, −45°), as shown in the image at right. In more general terms, they adopt dihedral angles such that the ψ dihedral angle of one residue and the φ dihedral angle of the next residue sum to roughly −105°. As a consequence, α-helical dihedral angles, in general, fall on a diagonal stripe on the Ramachandran diagram (of slope −1), ranging from (−90°, −15°) to (−35°, −70°). For comparison, the sum of the dihedral angles for a 310 helix is roughly −75°, whereas that for the π-helix is roughly −130°. The general formula for the rotation angle Ω per residue of any polypeptide helix with trans isomers is given by the equation[12]

3 cos Ω = 1 − 4 cos2 φ + ψ/2

The α-helix is tightly packed; there is almost no free space within the helix. The amino-acid side-chains are on the outside of the helix, and point roughly "downward" (i.e., toward the N-terminus), like the branches of an evergreen tree (Christmas tree effect). This directionality is sometimes used in preliminary, low-resolution electron-density maps to determine the direction of the protein backbone.[13]

2D (2-dimensional) diagrams for representing α-helices

Helical wheel diagram
Wenxiang diagram

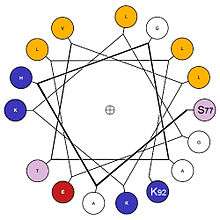
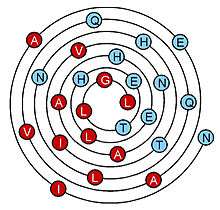
Three differently arranged styles of 2D diagrams are used to represent different aspects of the sequence and structure relationships that confer specific physical and interaction properties on individual α-helices. Two of these emphasize circular placement around the cylindrical cross-section: The first-developed such diagram is called the "helical wheel",[14] and a more recent version is called the "wenxiang diagram".[15] The latter name came from the fact that it resembles a coil-like incense used in China to repel mosquitos (Chinese: 蚊香; pinyin: wénxiāng).

The helical wheel represents a helix by a projection of the Cα backbone structure down the helix axis, while the wenxiang diagram represents it more abstractly as a smooth spiral coiled on the plane of the page. Both label the sequence with one-letter amino-acid code (see amino acid) at each Cα position, using different colors or symbols to code the amino-acid properties. Hydrophobic vs hydrophilic amino acids are always distinguished, as the most important property governing helix interactions. Sometimes positively vs negatively charged hydrophilics are distinguished, and sometimes ambiguous amino acids such as glycine (G) are distinguished. Color-coding conventions are various. The helical wheel does not change representation along the helix, while the wenxiang diagram is able to show the relative locations of the amino acids in an α-helix regardless of how long it is.

Either circular style of diagram can provide an intuitive and easily visualizable 2D picture that characterizes the disposition of hydrophobic and hydrophilic residues in α-helices,[14][15] and can be used to study helix–helix interactions,[16] helix-membrane interactions as quantified by the helical hydrophobic moment,[17] or protein-protein interactions.[18] [19] Various utilities and web sites are available to generate helical wheels, such as the page by Kael Fischer.[20]

The third style of 2D diagram is called a "helical net". It is generated by opening the cylindrical surface of each helix along a line parallel to the axis and laying the result out vertically. The helix net is not suitable for studying helix–helix packing interactions, but it has become the dominant means of representing the sequence arrangement for integral membrane proteins because it shows important relationships of the helical sequence to vertical positioning within the membrane even without knowledge of how the helices are arranged in 3D.

Stability

Helices observed in proteins can range from four to over forty residues long, but a typical helix contains about ten amino acids (about three turns). In general, short polypeptides do not exhibit much α-helical structure in solution, since the entropic cost associated with the folding of the polypeptide chain is not compensated for by a sufficient amount of stabilizing interactions. In general, the backbone hydrogen bonds of α-helices are considered slightly weaker than those found in β-sheets, and are readily attacked by the ambient water molecules. However, in more hydrophobic environments such as the plasma membrane, or in the presence of co-solvents such as trifluoroethanol (TFE), or isolated from solvent in the gas phase,[21] oligopeptides readily adopt stable α-helical structure. Furthermore, crosslinks can be incorporated into peptides to conformationally stabilize helical folds. Crosslinks stabilize the helical state by entropically destabilizing the unfolded state and by removing enthalpically stabilized "decoy" folds that compete with the fully helical state.[22] It has been shown that α-helices are more stable, robust to mutations and designable than β-strands in natural proteins[23], and also in artificial designed proteins.[24]

An α-helix in ultrahigh-resolution electron density contours, with oxygen atoms in red, nitrogen atoms in blue, and hydrogen bonds as green dotted lines (PDB file 2NRL, 17-32). The N-terminus is at the top, here.

Experimental determination

Since the α-helix is defined by its hydrogen bonds and backbone conformation, the most detailed experimental evidence for α-helical structure comes from atomic-resolution X-ray crystallography such as the example shown at right. It is clear that all the backbone carbonyl oxygens point downward (toward the C-terminus) but splay out slightly, and the H-bonds are approximately parallel to the helix axis. Protein structures from NMR spectroscopy also show helices well, with characteristic observations of nuclear Overhauser effect (NOE) couplings between atoms on adjacent helical turns. In some cases, the individual hydrogen bonds can be observed directly as a small scalar coupling in NMR.

There are several lower-resolution methods for assigning general helical structure. The NMR chemical shifts (in particular of the Cα, Cβ and C′) and residual dipolar couplings are often characteristic of helices. The far-UV (170–250 nm) circular dichroism spectrum of helices is also idiosyncratic, exhibiting a pronounced double minimum at around 208 and 222 nm. Infrared spectroscopy is rarely used, since the α-helical spectrum resembles that of a random coil (although these might be discerned by, e.g., hydrogen-deuterium exchange). Finally, cryo electron microscopy is now capable of discerning individual α-helices within a protein, although their assignment to residues is still an active area of research.

Long homopolymers of amino acids often form helices if soluble. Such long, isolated helices can also be detected by other methods, such as dielectric relaxation, flow birefringence, and measurements of the diffusion constant. In stricter terms, these methods detect only the characteristic prolate (long cigar-like) hydrodynamic shape of a helix, or its large dipole moment.

Amino-acid propensities

Different amino-acid sequences have different propensities for forming α-helical structure. Methionine, alanine, leucine, glutamate, and lysine uncharged ("MALEK" in the amino-acid 1-letter codes) all have especially high helix-forming propensities, whereas proline and glycine have poor helix-forming propensities.[25] Proline either breaks or kinks a helix, both because it cannot donate an amide hydrogen bond (having no amide hydrogen), and also because its sidechain interferes sterically with the backbone of the preceding turn – inside a helix, this forces a bend of about 30° in the helix's axis.[10] However, proline is often seen as the first residue of a helix, it is presumed due to its structural rigidity. At the other extreme, glycine also tends to disrupt helices because its high conformational flexibility makes it entropically expensive to adopt the relatively constrained α-helical structure.

Table of standard amino acid alpha-helical propensities

Estimated differences in free energy, Δ(ΔG), estimated in kcal/mol per residue in an α-helical configuration, relative to alanine arbitrarily set as zero. Higher numbers (more positive free energies) are less favoured. Significant deviations from these average numbers are possible, depending on the identities of the neighbouring residues.

Differences in free energy per residue[26]
Amino acid 3-
letter		 1-
letter		 Helical penalty
kcal/mol kJ/mol
Alanine Ala A 0.00 0.00
Arginine Arg R 0.21 0.88
Asparagine Asn N 0.65 2.72
Aspartic acid Asp D 0.69 2.89
Cysteine Cys C 0.68 2.85
Glutamic acid Glu E 0.40 1.67
Glutamine Gln Q 0.39 1.63
Glycine Gly G 1.00 4.18
Histidine His H 0.61 2.55
Isoleucine Ile I 0.41 1.72
Leucine Leu L 0.21 0.88
Lysine Lys K 0.26 1.09
Methionine Met M 0.24 1.00
Phenylalanine Phe F 0.54 2.26
Proline Pro P 3.16 13.22
Serine Ser S 0.50 2.09
Threonine Thr T 0.66 2.76
Tryptophan Trp W 0.49 2.05
Tyrosine Tyr Y 0.53 2.22
Valine Val V 0.61 2.55

Dipole moment

A helix has an overall dipole moment due to the aggregate effect of the individual microdipoles from the carbonyl groups of the peptide bond pointing along the helix axis.[27] The effects of this macrodipole are a matter of some controversy. α-helices often occur with the N-terminal end bound by a negatively charged group, sometimes an amino acid side chain such as glutamate or aspartate, or sometimes a phosphate ion. Some regard the helix macrodipole as interacting electrostatically with such groups. Others feel that this is misleading and it is more realistic to say that the hydrogen bond potential of the free NH groups at the N-terminus of an α-helix can be satisfied by hydrogen bonding; this can also be regarded as set of interactions between local microdipoles such as C=O···H−N.[28][29]

Coiled coils

Coiled-coil α helices are highly stable forms in which two or more helices wrap around each other in a "supercoil" structure. Coiled coils contain a highly characteristic sequence motif known as a heptad repeat, in which the motif repeats itself every seven residues along the sequence (amino acid residues, not DNA base-pairs). The first and especially the fourth residues (known as the a and d positions) are almost always hydrophobic; the fourth residue is typically leucine - this gives rise to the name of the structural motif called a leucine zipper, which is a type of coiled-coil. These hydrophobic residues pack together in the interior of the helix bundle. In general, the fifth and seventh residues (the e and g positions) have opposing charges and form a salt bridge stabilized by electrostatic interactions. Fibrous proteins such as keratin or the "stalks" of myosin or kinesin often adopt coiled-coil structures, as do several dimerizing proteins. A pair of coiled-coils – a four-helix bundle – is a very common structural motif in proteins. For example, it occurs in human growth hormone and several varieties of cytochrome. The Rop protein, which promotes plasmid replication in bacteria, is an interesting case in which a single polypeptide forms a coiled-coil and two monomers assemble to form a four-helix bundle.

The amino acids that make up a particular helix can be plotted on a helical wheel, a representation that illustrates the orientations of the constituent amino acids (see the article for leucine zipper for such a diagram). Often in globular proteins, as well as in specialized structures such as coiled-coils and leucine zippers, an α-helix will exhibit two "faces" – one containing predominantly hydrophobic amino acids oriented toward the interior of the protein, in the hydrophobic core, and one containing predominantly polar amino acids oriented toward the solvent-exposed surface of the protein.

Larger-scale assemblies

The Hemoglobin molecule has four heme-binding subunits, each made largely of α-helices.

Myoglobin and hemoglobin, the first two proteins whose structures were solved by X-ray crystallography, have very similar folds made up of about 70% α-helix, with the rest being non-repetitive regions, or "loops" that connect the helices. In classifying proteins by their dominant fold, the Structural Classification of Proteins database maintains a large category specifically for all-α proteins.

Hemoglobin then has an even larger-scale quaternary structure, in which the functional oxygen-binding molecule is made up of four subunits.

Functional roles

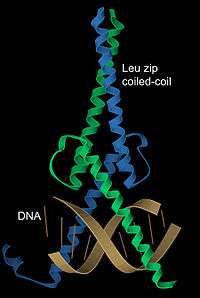
Leucine zipper coiled-coil helices & DNA-binding helices: transcription factor Max (PDB file 1HLO)
Bovine rhodopsin (PDB file 1GZM), with a bundle of seven helices crossing the membrane (membrane surfaces marked by horizontal lines)

DNA binding

α-Helices have particular significance in DNA binding motifs, including helix-turn-helix motifs, leucine zipper motifs and zinc finger motifs. This is because of the convenient structural fact that the diameter of an α-helix is about 12 Å (1.2 nm) including an average set of sidechains, about the same as the width of the major groove in B-form DNA, and also because coiled-coil (or leucine zipper) dimers of helices can readily position a pair of interaction surfaces to contact the sort of symmetrical repeat common in double-helical DNA.[30] An example of both aspects is the transcription factor Max (see image at left), which uses a helical coiled coil to dimerize, positioning another pair of helices for interaction in two successive turns of the DNA major groove.

Membrane spanning

α-Helices are also the most common protein structure element that crosses biological membranes (transmembrane protein)[31] it is presumed because the helical structure can satisfy all backbone hydrogen-bonds internally, leaving no polar groups exposed to the membrane if the sidechains are hydrophobic. Proteins are sometimes anchored by a single membrane-spanning helix, sometimes by a pair, and sometimes by a helix bundle, most classically consisting of seven helices arranged up-and-down in a ring such as for rhodopsins (see image at right) or for G protein–coupled receptors (GPCRs).

Mechanical properties

α-Helices under axial tensile deformation, a characteristic loading condition that appears in many alpha-helix-rich filaments and tissues, results in a characteristic three-phase behavior of stiff-soft-stiff tangent modulus.[32] Phase I corresponds to the small-deformation regime during which the helix is stretched homogeneously, followed by phase II, in which alpha-helical turns break mediated by the rupture of groups of H-bonds. Phase III is typically associated with large-deformation covalent bond stretching.

Dynamical features

Alpha-helices in proteins may have low-frequency accordion-like motion as observed by the Raman spectroscopy[33] and analyzed via the quasi-continuum model.[34][35] Helices not stabilized by tertiary interactions show dynamic behavior, which can be mainly attributed to helix fraying from the ends.[36]

Helix–coil transition

Homopolymers of amino acids (such as polylysine) can adopt α-helical structure at low temperature that is "melted out" at high temperatures. This helix–coil transition was once thought to be analogous to protein denaturation. The statistical mechanics of this transition can be modeled using an elegant transfer matrix method, characterized by two parameters: the propensity to initiate a helix and the propensity to extend a helix.

The α-helix in art

Julian Voss-Andreae's Alpha Helix for Linus Pauling (2004), powder coated steel, height 10 ft (3 m). The sculpture stands in front of Pauling's childhood home on 3945 SE Hawthorne Boulevard in Portland, Oregon, USA.

At least five artists have made explicit reference to the α-helix in their work: Julie Newdoll in painting and Julian Voss-Andreae, Bathsheba Grossman, Byron Rubin, and Mike Tyka in sculpture.

San Francisco area artist Julie Newdoll,[37] who holds a degree in Microbiology with a minor in art, has specialized in paintings inspired by microscopic images and molecules since 1990. Her painting "Rise of the Alpha Helix" (2003) features human figures arranged in an α helical arrangement. According to the artist, "the flowers reflect the various types of sidechains that each amino acid holds out to the world".[37] It is interesting to note that this same metaphor is also echoed from the scientist's side: "β sheets do not show a stiff repetitious regularity but flow in graceful, twisting curves, and even the α-helix is regular more in the manner of a flower stem, whose branching nodes show the influence of environment, developmental history, and the evolution of each part to match its own idiosyncratic function."[10]

Julian Voss-Andreae is a German-born sculptor with degrees in experimental physics and sculpture. Since 2001 Voss-Andreae creates "protein sculptures"[38] based on protein structure with the α-helix being one of his preferred objects. Voss-Andreae has made α-helix sculptures from diverse materials including bamboo and whole trees. A monument Voss-Andreae created in 2004 to celebrate the memory of Linus Pauling, the discoverer of the α-helix, is fashioned from a large steel beam rearranged in the structure of the α-helix. The 10-foot-tall (3 m), bright-red sculpture stands in front of Pauling's childhood home in Portland, Oregon.

Ribbon diagrams of α-helices are a prominent element in the laser-etched crystal sculptures of protein structures created by artist Bathsheba Grossman, such as those of insulin, hemoglobin, and DNA polymerase.[39] Byron Rubin is a former protein crystallographer now professional sculptor in metal of proteins, nucleic acids, and drug molecules - many of which featuring α-helices, such as subtilisin, human growth hormone, and phospholipase A2.[40]

Mike Tyka is a computational biochemist at the University of Washington working with David Baker. Tyka has been making sculptures of protein molecules since 2010 from copper and steel, including ubiquitin and a potassium channel tetramer.[41]

See also

References

  1. ↑ Kendrew JC, Dickerson RE, Strandberg BE, Hart RG, Davies DR, Phillips DC, Shore VC (February 1960). "Structure of myoglobin: A three-dimensional Fourier synthesis at 2 Å resolution". Nature. 185 (4711): 422–7. Bibcode:1960Natur.185..422K. PMID 18990802. doi:10.1038/185422a0.
  2. ↑ Neurath H (1940). "Intramolecular folding of polypeptide chains in relation to protein structure". Journal of Physical Chemistry. 44 (3): 296–305. doi:10.1021/j150399a003.
  3. ↑ Taylor HS (1942). "Large molecules through atomic spectacles". Proceedings of the American Philosophical Society. 85: 1–12. JSTOR 985121.
  4. ↑ Huggins M (1943). "The structure of fibrous proteins". Chemical Reviews. 32 (2): 195–218. doi:10.1021/cr60102a002.
  5. ↑ Bragg WL, Kendrew JC, Perutz MF (1950). "Polypeptide chain configurations in crystalline proteins". Proceedings of the Royal Society A. 203 (1074): 321–?. Bibcode:1950RSPSA.203..321B. doi:10.1098/rspa.1950.0142.
  6. ↑ Pauling L, Corey RB, Branson HR (April 1951). "The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain". Proceedings of the National Academy of Sciences of the United States of America. 37 (4): 205–11. Bibcode:1951PNAS...37..205P. PMC 1063337 Freely accessible. PMID 14816373. doi:10.1073/pnas.37.4.205.
  7. ↑ Dunitz J (2001). "Pauling's Left-Handed α-Helix". Angewandte Chemie International Edition. 40 (22): 4167–4173. doi:10.1002/1521-3773(20011119)40:22<4167::AID-ANIE4167>3.0.CO;2-Q.
  8. ↑ IUPAC-IUB Commission on Biochemical Nomenclature (1970). "Abbreviations and symbols for the description of the conformation of polypeptide chains". Journal of Biological Chemistry. 245: 6489–6497.
  9. ↑ Kabsch W, Sander C (December 1983). "Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features". Biopolymers. 22 (12): 2577–637. PMID 6667333. doi:10.1002/bip.360221211.
  10. 1 2 3 Richardson JS (1981). "The anatomy and taxonomy of protein structure". Advances in Protein Chemistry. 34: 167–339. PMID 7020376. doi:10.1016/S0065-3233(08)60520-3.
  11. ↑ Lovell SC, Davis IW, Arendall WB, de Bakker PI, Word JM, Prisant MG, Richardson JS, Richardson DC (February 2003). "Structure validation by Calpha geometry: phi,psi and Cbeta deviation". Proteins. 50 (3): 437–50. PMID 12557186. doi:10.1002/prot.10286.
  12. ↑ Dickerson RE, Geis I (1969), Structure and Action of Proteins, Harper, New York
  13. ↑ Terwilliger TC (March 2010). "Rapid model building of alpha-helices in electron-density maps". Acta Crystallographica. Section D, Biological Crystallography. 66 (Pt 3): 268–75. PMC 2827347 Freely accessible. PMID 20179338. doi:10.1107/S0907444910000314.
  14. 1 2 Schiffer M, Edmundson AB (March 1967). "Use of helical wheels to represent the structures of proteins and to identify segments with helical potential". Biophysical Journal. 7 (2): 121–35. Bibcode:1967BpJ.....7..121S. PMC 1368002 Freely accessible. PMID 6048867. doi:10.1016/S0006-3495(67)86579-2.
  15. 1 2 Chou KC, Zhang CT, Maggiora GM (May 1997). "Disposition of amphiphilic helices in heteropolar environments". Proteins. 28 (1): 99–108. PMID 9144795. doi:10.1002/(SICI)1097-0134(199705)28:1<99::AID-PROT10>3.0.CO;2-C.
  16. ↑ Kurochkina N (May 2010). "Helix-helix interactions and their impact on protein motifs and assemblies". Journal of Theoretical Biology. 264 (2): 585–92. PMID 20202472. doi:10.1016/j.jtbi.2010.02.026.
  17. ↑ Eisenberg D, Weiss RM, Terwilliger TC (1982). "The helical hydrophobic moment: a measure of the amphiphilicity of a helix". Nature. 299 (5881): 371–4. Bibcode:1982Natur.299..371E. PMID 7110359. doi:10.1038/299371a0.
  18. ↑ Zhou GP (September 2011). "The disposition of the LZCC protein residues in wenxiang diagram provides new insights into the protein-protein interaction mechanism". Journal of Theoretical Biology. 284 (1): 142–8. PMID 21718705. doi:10.1016/j.jtbi.2011.06.006.
  19. ↑ Zhou GP (2011). "The Structural Determinations of the Leucine Zipper Coiled-Coil Domains of the cGMP-Dependent Protein Kinase I alpha and its Interaction with the Myosin Binding Subunit of the Myosin Light Chains Phosphase". Protein & Peptide Letters. 18 (10): 966–978. PMID 21592084. doi:10.2174/0929866511107010966.
  20. ↑ .
  21. ↑ Hudgins RR, Jarrold MF (1999). "Helix Formation in Unsolvated Alanine-Based Peptides: Helical Monomers and Helical Dimers". Journal of the American Chemical Society. 121 (14): 3494–3501. doi:10.1021/ja983996a.
  22. ↑ Kutchukian PS, Yang JS, Verdine GL, Shakhnovich EI (April 2009). "All-atom model for stabilization of alpha-helical structure in peptides by hydrocarbon staples". Journal of the American Chemical Society. 131 (13): 4622–7. PMC 2735086 Freely accessible. PMID 19334772. doi:10.1021/ja805037p.
  23. ↑ Abrusan G, Marsh JA (2016). "Alpha helices are more robust to mutations than beta strands". PLoS Computational Biology. 12 (12): 1–16. PMID 27935949. doi:10.1371/journal.pcbi.1005242.
  24. ↑ Rocklin GJ, et al. (2017). "Global analysis of protein folding using massively parallel design, synthesis, and testing". Science. 357 (6347): 168–175. PMID 28706065. doi:10.1126/science.aan0693.
  25. ↑ Pace CN, Scholtz JM (July 1998). "A helix propensity scale based on experimental studies of peptides and proteins". Biophysical Journal. 75 (1): 422–7. Bibcode:1998BpJ....75..422N. PMC 1299714 Freely accessible. PMID 9649402. doi:10.1016/S0006-3495(98)77529-0.
  26. ↑ Pace, C. Nick; Scholtz, J. Martin (1998). "A Helix Propensity Scale Based on Experimental Studies of Peptides and Proteins". Biophysical Journal. 75. pp. 422–427. doi:10.1016/s0006-3495(98)77529-0.
  27. ↑ Hol WG, van Duijnen PT, Berendsen HJ (1978). "The alpha helix dipole and the properties of proteins". Nature. 273: 443–446. Bibcode:1978Natur.273..443H. doi:10.1038/273443a0.
  28. ↑ He JJ, Quiocho FA (October 1993). "Dominant role of local dipoles in stabilizing uncompensated charges on a sulfate sequestered in a periplasmic active transport protein". Protein Science. 2 (10): 1643–7. PMC 2142251 Freely accessible. PMID 8251939. doi:10.1002/pro.5560021010.
  29. ↑ Milner-White EJ (November 1997). "The partial charge of the nitrogen atom in peptide bonds". Protein Science. 6 (11): 2477–82. PMC 2143592 Freely accessible. PMID 9385654. doi:10.1002/pro.5560061125.
  30. ↑ Branden & Tooze, chapter 10
  31. ↑ Branden & Tooze, chapter 12.
  32. ↑ Ackbarow T, Chen X, Keten S, Buehler MJ (October 2007). "Hierarchies, multiple energy barriers, and robustness govern the fracture mechanics of alpha-helical and beta-sheet protein domains". Proceedings of the National Academy of Sciences of the United States of America. 104 (42): 16410–5. Bibcode:2007PNAS..10416410A. PMC 2034213 Freely accessible. PMID 17925444. doi:10.1073/pnas.0705759104.
  33. ↑ Painter PC, Mosher LE, Rhoads C (July 1982). "Low-frequency modes in the Raman spectra of proteins". Biopolymers. 21 (7): 1469–72. PMID 7115900. doi:10.1002/bip.360210715.
  34. ↑ Chou KC (December 1983). "Identification of low-frequency modes in protein molecules". The Biochemical Journal. 215 (3): 465–9. PMC 1152424 Freely accessible. PMID 6362659. doi:10.1042/bj2150465.
  35. ↑ Chou KC (May 1984). "Biological functions of low-frequency vibrations (phonons). III. Helical structures and microenvironment". Biophysical Journal. 45 (5): 881–9. Bibcode:1984BpJ....45..881C. PMC 1434967 Freely accessible. PMID 6428481. doi:10.1016/S0006-3495(84)84234-4.
  36. ↑ Fierz B, Reiner A, Kiefhaber T (January 2009). "Local conformational dynamics in alpha-helices measured by fast triplet transfer". Proceedings of the National Academy of Sciences of the United States of America. 106 (4): 1057–62. Bibcode:2009PNAS..106.1057F. PMC 2633579 Freely accessible. PMID 19131517. doi:10.1073/pnas.0808581106.
  37. 1 2 "Julie Newdoll Scientifically Inspired Art, Music, Board Games". www.brushwithscience.com. Retrieved 2016-04-06.
  38. ↑ Voss-Andreae J (2005). "Protein Sculptures: Life's Building Blocks Inspire Art". Leonardo. 38: 41–45. doi:10.1162/leon.2005.38.1.41.
  39. ↑ Grossman, Bathsheba. "Bathsheba Sculpture - About the Artist". www.bathsheba.com. Retrieved 2016-04-06.
  40. ↑ "About". molecularsculpture.com. Retrieved 2016-04-06.
  41. ↑ Tyka, Mike. "About". www.miketyka.com. Retrieved 2016-04-06.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.