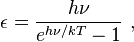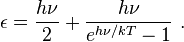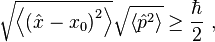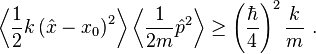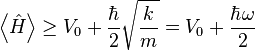Zero-point energy

Zero-point energy, also called quantum vacuum zero-point energy, is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state.

All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature. The uncertainty principle requires every physical system to have a zero-point energy greater than the minimum of its classical potential well. This results in motion even at absolute zero. For example, liquid helium does not freeze under atmospheric pressure at any temperature because of its zero-point energy.

The concept of zero-point energy was developed by Max Planck in Germany in 1911 as a corrective term added to a zero-grounded formula developed in his original quantum theory in 1900.[1] The term zero-point energy is a translation from the German Nullpunktsenergie.[2]:275ff

Vacuum energy is the zero-point energy of all the fields in space, which in the Standard Model includes the electromagnetic field, other gauge fields, fermionic fields, and the Higgs field. It is the energy of the vacuum, which in quantum field theory is defined not as empty space but as the ground state of the fields. In cosmology, the vacuum energy is one possible explanation for the cosmological constant.[3] A related term is zero-point field, which is the lowest energy state of a particular field.[4]

Scientists are not in agreement about how much energy is contained in the vacuum. Quantum mechanics requires the energy to be large as Paul Dirac claimed it is, like a sea of energy. Other scientists specializing in General Relativity require the energy to be small enough for curvature of space to agree with observed astronomy. The Heisenberg uncertainty principle allows the energy to be as large as needed to promote quantum actions for a brief moment of time, even if the average energy is small enough to satisfy relativity and flat space. To cope with disagreements, the vacuum energy is described as a virtual energy potential of positive and negative energy.[5]

History

In 1900, Max Planck derived the average energy of a single energy radiator, e.g., a vibrating atomic unit, as a function of absolute temperature:[6]

\epsilon = \frac{h\nu}{ e^{h\nu/kT}-1} ~,

where h is Planck's constant, ν is the frequency, k is Boltzmann's constant, and T is the absolute temperature.

In a series of works from 1911 to 1913, Planck proposed his second quantum theory, in which he introduced the zero-point energy. Only the emitted radiation was attributed to discrete energy quanta, while the absorbed radiation could be continuous in energy. From these ideas, he found that the average energy of an oscillator is[1]:sec 2[7]:235ff

\epsilon =\frac{h\nu}{2} + \frac{h\nu}{e^{h\nu/kT}-1} ~.

Soon, the idea of zero-point energy attracted the attention of Albert Einstein and his assistant Otto Stern. They attempted to prove the existence of zero-point energy by calculating the specific heat of hydrogen gas and compared it with the experimental data. However, after assuming they had succeeded and after publishing the findings, they retracted the support of the idea because they found Planck's second theory may not apply to their example.[2]:270ff

In 1916 Walther Nernst proposed that empty space was filled with zero-point electromagnetic radiation.[1]:sec 4 Then in 1925, the existence of zero-point energy was shown to be “required by quantum mechanics, as a direct consequence of Heisenberg's uncertainty principle” in Werner Heisenberg's famous article "Quantum theoretical re-interpretation of kinematic and mechanical relations".[8]:162

Relation to the uncertainty principle

Zero-point energy is fundamentally related to the Heisenberg uncertainty principle.[9] Roughly speaking, the uncertainty principle states that complementary variables (such as a particle's position and momentum, or a field's value and derivative at a point in space) cannot simultaneously be specified precisely by any given quantum state. In particular, there cannot exist a state in which the system simply sits motionless at the bottom of its potential well: for, then, its position and momentum would both be completely determined to arbitrarily great precision. Therefore, instead, the lowest-energy state (the ground state) of the system must have a distribution in position and momentum that satisfies the uncertainty principle−−which implies its energy must be greater than the minimum of the potential well.

Near the bottom of a potential well, the Hamiltonian of a general system (the quantum-mechanical operator giving its energy) can be approximated as a quantum harmonic oscillator,

\hat{H} = V_0 + \frac{1}{2} k \left(\hat{x} - x_0\right)^2 + \frac{1}{2m} \hat{p}^2~,

where V0 is the minimum of the classical potential well.

The uncertainty principle tells us that

\sqrt{\left\langle \left(\hat{x} - x_0\right)^2 \right\rangle} \sqrt{\left\langle \hat{p}^2 \right\rangle} \geq \frac{\hbar}{2}~,

making the expectation values of the kinetic and potential terms above satisfy

\left\langle \frac{1}{2} k \left(\hat{x} - x_0\right)^2 \right\rangle \left\langle \frac{1}{2m} \hat{p}^2 \right\rangle \geq \left(\frac{\hbar}{4}\right)^2 \frac{k}{m}~.

The expectation value of the energy must therefore be at least

\left\langle \hat{H} \right\rangle \geq V_0 + \frac{\hbar}{2} \sqrt{\frac{k}{m}} = V_0 + \frac{\hbar \omega}{2}

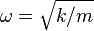where \omega = \sqrt{k/m} is the angular frequency at which the system oscillates.

A more thorough treatment, showing that the energy of the ground state actually saturates this bound and is exactly E0=V0+ħω/2, requires solving for the ground state of the system.

Varieties

The concept of zero-point energy occurs in a number of situations.

In ordinary quantum mechanics, the zero-point energy is the energy associated with the ground state of the system. The professional physics literature tends to measure frequency, as denoted by ν above, using angular frequency, denoted with ω and defined by ω=2πν. This leads to a convention of writing Planck's constant h with a bar through its top (ħ) to denote the quantity h/2π. In these terms, the most famous such example of zero-point energy is the above E=ħω/2 associated with the ground state of the quantum harmonic oscillator. In quantum mechanical terms, the zero-point energy is the expectation value of the Hamiltonian of the system in the ground state.

The zero-point energy E=ħω/2 causes the ground-state of an harmonic oscillator to advance its phase (color). This has measurable effects when several eigenstates are superimposed.

In quantum field theory, the fabric of space is visualized as consisting of fields, with the field at every point in space and time being a quantum harmonic oscillator, with neighboring oscillators interacting. In this case, one has a contribution of E=ħω/2 from every point in space, resulting in a calculation of infinite zero-point energy in any finite volume; this is one reason renormalization is needed to make sense of quantum field theories. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.

In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations, or the zero-point energy to the particle masses.

Experimental observations

A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect, proposed in 1948 by Dutch physicist Hendrik B. G. Casimir (Philips Research), who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move. This force has been measured and found to be in good agreement with the theory. However, there is still some debate on whether vacuum energy is necessary to explain the Casimir effect. Robert Jaffe of MIT argues that the Casimir force should not be considered evidence for vacuum energy, since it can be derived in QED without reference to vacuum energy by considering charge-current interactions (the radiation-reaction picture).[10]

The experimentally measured Lamb shift has been argued to be, in part, a zero-point energy effect.[11]

Gravitation and cosmology

Unsolved problem in physics:
Why doesn't the zero-point energy density of the vacuum change with changes in the volume of the universe? And related to that, why doesn't the large constant zero-point energy density of the vacuum cause a large cosmological constant? What cancels it out?
(more unsolved problems in physics)

In cosmology, the zero-point energy offers an intriguing possibility for explaining the speculative positive values of the proposed cosmological constant. [12] In brief, if the energy is "really there", then it should exert a gravitational force.[13] In general relativity, mass and energy are equivalent; both produce a gravitational field. One obvious difficulty with this association is that the zero-point energy of the vacuum is absurdly large. Naively, it is infinite, because it includes the energy of waves with arbitrarily short wavelengths. But since only differences in energy are physically measurable, the infinity can be removed by renormalization. In all practical calculations, this is how the infinity is handled. It is also arguable that undiscovered physics relevant at the Planck scale reduces or eliminates the energy of waves shorter than the Planck length, making the total zero-point energy finite.

Utilization controversy

As a scientific concept, the existence of zero-point energy is not controversial. However, the ability to harness zero point energy for useful work is considered pseudoscience by the scientific community at large.[14][15] Zero-point energy is, by definition, a minimum energy below which a thermodynamic system can never go.[14] Thus, none of this energy can be withdrawn without altering the system to a different form in which the system has a lower zero-point energy. [16] Nevertheless, there have been numerous claims of devices capable of extracting usable zero-point energy. None of these claims has ever been validated by the scientific community.[17]

Science skeptic and writer, Martin Gardner has called claims of such zero-point-energy-based systems, "as hopeless as past efforts to build perpetual motion machines"[18] A perpetual motion machine is a device that can operate indefinitely, with optional output of excess energy, without any source of fuel. Such a device would violate the laws of thermodynamics. Despite the science, numerous articles and books have been published addressing and discussing the potential of tapping zero-point-energy from the quantum vacuum or elsewhere. Examples of such are the work of the following authors: Claus Wilhelm Turtur,[19] Jeane Manning, Joel Garbon,[20] John Bedini,[21] Tom Bearden,[22][23][24] Thomas Valone,[25][26][27] Moray B King,[28][29][30] Christopher Toussaint, Bill Jenkins,[31] Nick Cook[32] and William James.[33]

The calculation that underlies the Casimir experiment, a calculation based on the formula predicting infinite vacuum energy, shows the zero-point energy of a system consisting of a vacuum between two plates will decrease at a finite rate as the two plates are drawn together. The vacuum energies are predicted to be infinite, but the changes are predicted to be finite. Casimir combined the projected rate of change in zero-point energy with the principle of conservation of energy to predict a force on the plates. The predicted force, which is very small and was experimentally measured to be within 5% of its predicted value, is finite.[34] Even though the zero-point energy is theoretically infinite, there is no evidence to suggest that infinite amounts of zero-point energy are available for use, that zero-point energy can be withdrawn for free, or that zero-point energy can be used in violation of conservation of energy.[35]

While unrelated to energy generation, there is a somewhat realistic potential for the utilization of zero-point energy in the design of extremely small scale devices like MEMS and NEMS.[14]

A document released by the NGIC shows there is ongoing worldwide research into zero-point energy, particular in China, Germany, Russia and Brazil.[14]

In popular culture

"Zero point energy" has been invoked in science fiction movies and video games, often as an explanation for "impossible" technology that provides free energy or otherwise contradicts known laws of physics.

In Disney/Pixar's animated film The Incredibles, the main villain Syndrome refers to his weapons as using zero-point energy.[36][37] The fan fiction community devoted to the character is named "Zero Point" because of this.[38]

In the TV show Stargate Atlantis, Zero Point Modules are advanced power sources built by the Ancients to power their cities and outposts. Weighing only a few kilograms,[39] a single ZPM can power the entire city of Atlantis for thousands of years. ZPMs supposedly extract vacuum energy from a small artificially-created region of subspace,[40] based on the concept of zero-point energy.[41] ZPMs are depicted as more powerful and efficient than fictional Naquadah generators or any conventional energy source on present day Earth.[40]

Notes

  1. 1 2 3 Kragh, Helge (2012). "Preludes to dark energy: zero-point energy and vacuum speculations". Archive for History of Exact Sciences (Springer-Verlag) 66 (3): 199–240. doi:10.1007/s00407-011-0092-3.
  2. 1 2 Albert Einstein (1995). Martin J. Klein; et al., eds. The Collected Papers of Albert Einstein, Volume 4: The Swiss Years: Writings, 1912-1914. Princeton University Press. ISBN 9780691037059.
  3. ↑ Rugh, S. E.; Zinkernagel, H. (2002). "The Quantum Vacuum and the Cosmological Constant Problem". Studies in History and Philosophy of Modern Physics, vol. 33 (4): 663–705. arXiv:hep-th/0012253. doi:10.1016/S1355-2198(02)00033-3.
  4. ↑ Gribbin, J. (1998). Q is for Quantum: An Encyclopedia of Particle Physics. Touchstone Books. ISBN 0-684-86315-4.
  5. ↑ Peskin, M. E.; Schroeder, D. V. (1995). An introduction to quantum field theory. Addison-Wesley. pp. 786–791. ISBN 978-0-201-50397-5.
  6. ↑ Planck, M (1900). "Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum". Verhandlungen der Deutschen Physikalischen Gesellschaft 2: 237–245.
  7. ↑ Thomas S. Kuhn. Black-Body Theory and the Quantum Discontinuity, 1894-1912. University of Chicago Press. ISBN 978-0-226-45800-7.
  8. ↑ Kragh, Helge (2002). Quantum Generations: A History of Physics in the Twentieth Century (Reprint ed.). Princeton University Press. ISBN 978-0691095523.
  9. ↑ W. Heisenberg (1927). [Original work as HTML "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik"] Check |url= value (help). Zeitschrift für Physik 43 (3): 172–198. Bibcode:1927ZPhy...43..172H. doi:10.1007/BF01397280
  10. ↑ Jaffe, R. L. (2005). "Casimir effect and the quantum vacuum". Physical Review D 72 (2): 021301. arXiv:hep-th/0503158. Bibcode:2005PhRvD..72b1301J. doi:10.1103/PhysRevD.72.021301.
  11. ↑ Hawton, M. (1993). "Self-consistent frequencies of the electron-photon system". Physical Review A 48 (3): 1824. Bibcode:1993PhRvA..48.1824H. doi:10.1103/PhysRevA.48.1824.
  12. ↑ Tarkowski, W. (2004). "A Toy Model of the Five-Dimensional Universe with the Cosmological Constant". International Journal of Modern Physics A 19 (29): 5051. arXiv:gr-qc/0407024. Bibcode:2004IJMPA..19.5051T. doi:10.1142/S0217751X04019366.
  13. ↑ Zee, A. (2008). "Gravity and Its Mysteries: Some Thoughts and Speculations" (PDF). AAPPS Bulletin 18 (4): 32.
  14. 1 2 3 4 Amber M. Aiken, Ph.D. "Zero-Point Energy: Can We Get Something From Nothing?" (PDF). U.S. Army National Ground Intelligence Center. Forays into "free energy" inventions and perpetual-motion machines using ZPE are considered by the broader scientific community to be pseudoscience.
  15. ↑ Zero-point energy, on season 8 , episode 2 of Scientific American Frontiers.
  16. ↑ "FOLLOW-UP: What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy?". Scientific American. 18 August 1997.
  17. ↑ Matt Visser (3 October 1996). "What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy?". Phlogistin / Scientific American Magazine. Archived from the original on August 18, 1997. Retrieved 31 May 2013.
  18. ↑ Martin Gardner, "'Dr' Bearden's Vacuum Energy", Skeptical Inquirer, January/February 2007
  19. ↑ Claus Wilhelm Turtur. Conversion of the zero-point energy of the quantum vacuum into classical mechanical energy (PDF). Bremen Europ. Hochsch.-Verl. Archived from the original on 2010.
  20. ↑ Jeane Manning, Joel Garbon. Breakthrough power : how quantum-leap new energy inventions can transform our world. Amber Bridge Books.
  21. ↑ John Bedini, Tom Bearden. Free energy generation : circuits & schematics. Cheniere Press.
  22. ↑ Tom Bearden. Energy from the vacuum : concepts & principles. Cheniere Press.
  23. ↑ Tom Bearden. Clash of the geniuses : inventing the impossible. New Science Ideas.
  24. ↑ Tom Bearden. Virtual State Engineering and Its Implications. Ft. Belvoir Defense Technical Information Center.
  25. ↑ Thomas Valone. Practical conversion of zero-point energy : feasibility study of the extraction of zero-point energy from the quantum vacuum for the performance of useful work. Integrity Research Institute.
  26. ↑ Thomas Valone. Zero point energy : the fuel of the future. Integrity Research Institute.
  27. ↑ Thomas Valone. Future energy : proceedings of the First International Conference on Future Energy. Integrity Research Institute.
  28. ↑ Moray B King. Tapping the zero-point energy : how free energy and anti-gravity might be possible with today's physics. Adventures Unlimited.
  29. ↑ Moray B King. Quest for zero point energy : engineering principles for 'free energy' inventions. Adventures Unlimited.
  30. ↑ Moray B King. The energy machine of T. Henry Moray : zero-point energy & pulsed plasma physics. Adventures Unlimited.
  31. ↑ Christopher Toussaint, Bill Jenkins. Free energy : the race to zero point. Lightworks Audio & Video.
  32. ↑ Nick Cook. The hunt for zero point : inside the classified world of antigravity technology. Broadway Books.
  33. ↑ William James. Zero point : power of the gods. Bloomington.
  34. ↑ "What is the Casimir Effect?".
  35. ↑ "FOLLOW-UP: What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy?". Scientific American. 18 August 1997.
  36. ↑ "Buddy Pine character profile". Retrieved 5 September 2012.
  37. ↑ "Zero Point Energy". Retrieved 5 September 2012.
  38. ↑ "Zero Point at FanFiction.net". Retrieved 5 September 2012.
  39. ↑ Stargate SG-1: The DVD Collection 52
  40. 1 2 "The Rising" (Stargate Atlantis)
  41. ↑ "Zero Point Energy goes Hollywood!". Retrieved 2008-03-14.

Bibliography

External links

Listen to this article (info/dl)


This audio file was created from a revision of the "Zero-point energy" article dated 2006-12-09, and does not reflect subsequent edits to the article. (Audio help)
More spoken articles

This article is issued from Wikipedia - version of the Thursday, February 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.