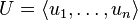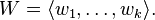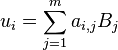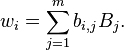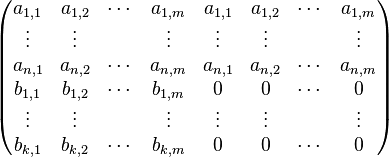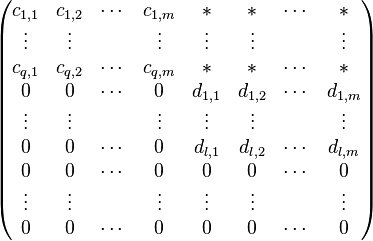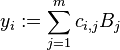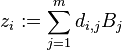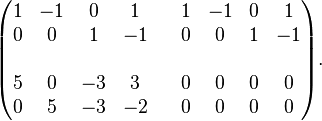Zassenhaus algorithm
In mathematics, the Zassenhaus algorithm[1] is a method to calculate a basis for the intersection and sum of two subspaces of a vector space. It is named after Hans Zassenhaus, but no publication of this algorithm by him is known.[2] It is used in computer algebra systems.[3]
Algorithm
Input
Let V be a vector space and U, W two finite-dimensional subspaces of V with the following spanning sets:
and
Finally, let 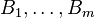 be linearly independent vectors so that
be linearly independent vectors so that  and
and  can be written as
can be written as
and
Output
The algorithm computes the base of the sum 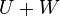 and a base of the intersection
and a base of the intersection 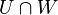 .
.
Algorithm
The algorithm creates the following block matrix of size 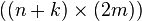 :
:
Using elementary row operations, this matrix is transformed to the row echelon form. Then, it has the following shape:
Here,  stands for arbitrary numbers, and the vectors
stands for arbitrary numbers, and the vectors
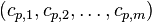 for every
for every 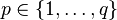 and
and 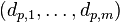 for every
for every 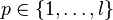 are nonzero.
are nonzero.
Then 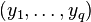 with
with
is a basis of 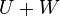 and
and 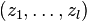 with
with
is a basis of 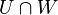 .
.
Proof of correctness
First, we define 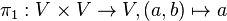 to be the projection to the first component.
to be the projection to the first component.
Let
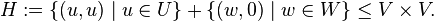 Then
Then 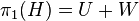 and
and
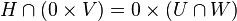 .
.
Also, 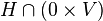 is the kernel of
is the kernel of 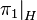 , the projection restricted to H.
Therefore,
, the projection restricted to H.
Therefore, 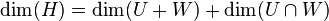 .
.
The Zassenhaus Algorithm calculates a basis of H. In the first m columns of this matrix, there is a basis 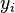 of
of 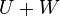 .
.
The rows of the form 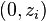 (with
(with 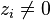 ) are obviously in
) are obviously in 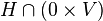 . Because the matrix is in row echelon form, they also linearly independent.
All rows which are different from zero (
. Because the matrix is in row echelon form, they also linearly independent.
All rows which are different from zero (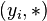 and
and 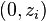 ) are a basis of H, so there are
) are a basis of H, so there are 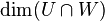 such
such  s. Therefore, the
s. Therefore, the  s form a basis of
s form a basis of 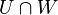 .
.
Example
Consider the two subspaces 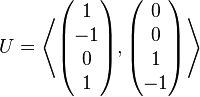 and
and 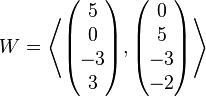 of the vector space
of the vector space  .
.
Using the standard basis, we create the following matrix of dimension 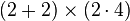 :
:
Using elementary row operations, we transform this matrix into the following matrix:
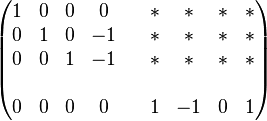 (some entries have been replaced by "
(some entries have been replaced by " " because they are irrelevant to the result).
" because they are irrelevant to the result).
Therefore,
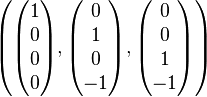 is a basis of
is a basis of 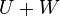 , and
, and
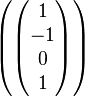 is a basis of
is a basis of 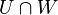 .
.
References
- ↑ Luks, Eugene M.; Rákóczi, Ferenc; Wright, Charles R. B. (April 1997), "Some algorithms for nilpotent permutation groups", Journal of Symbolic Computation 23 (4): 335–354, doi:10.1006/jsco.1996.0092.
- ↑ Fischer, Gerd (2012), Lernbuch Lineare Algebra und Analytische Geometrie (in German), Vieweg+Teubner, pp. 207–210, doi:10.1007/978-3-8348-2379-3, ISBN 978-3-8348-2378-6
- ↑ The GAP Group (February 13, 2015), "24 Matrices", GAP Reference Manual, Release 4.7, retrieved 2015-06-11
External links
- "Mathematik-Online-Lexikon: Zassenhaus-Algorithmus" (in German). Retrieved 2012-09-15.