Zariski's main theorem

In algebraic geometry, Zariski's main theorem, proved by Oscar Zariski (1943), is a statement about the structure of birational morphisms stating roughly that there is only one branch at any normal point of a variety. It is the special case of Zariski's connectedness theorem when the two varieties are birational.

Zariski's main theorem can be stated in several ways which at first sight seem to be quite different, but are in fact deeply related. Some of the variations that have been called Zariski's main theorem are as follows:

The name "Zariski's main theorem" comes from the fact that Zariski labelled it as the "MAIN THEOREM" in Zariski (1943).

Zariski's main theorem for birational morphisms

Let f be a birational mapping of algebraic varieties V and W. Recall that f is defined by a closed subvariety \Gamma \subset V \times W (a "graph" of f) such that the projection on the first factor p_1 induces an isomorphism between an open U \subset V and p_1^{-1}(U), and such that p_2 \circ p_1^{-1} is an isomorphism on U too. The complement of U in V is called a fundamental variety or indeteminancy locus, and an image of a subset of V under p_2 \circ p_1^{-1} is called a total transform of it.

The original statement of the theorem in (Zariski 1943, p. 522) reads:

MAIN THEOREM: If W is an irreducible fundamental variety on V of a birational correspondence T between V and V′ and if T has no fundamental elements on V′ then — under the assumption that V is locally normal at W — each irreducible component of the transform T[W] is of higher dimension than W.

Here T is essentially a morphism from V′ to V that is birational, W is a subvariety of the set where the inverse of T is not defined whose local ring is normal, and the transform T[W] means the inverse image of W under the morphism from V′ to V.

Here are some variants of this theorem stated using more recent terminology. Hartshorne (1977, Corollary III.11.4) calls the following connectedness statement "Zariski's Main theorem":

If f:X→Y is a birational projective morphism between noetherian integral schemes, then the inverse image of every normal point of Y is connected.

The following consequence of it (Theorem V.5.2,loc.cit.) also goes under this name:

If f:X→Y is a birational transformation of projective varieties with Y normal, then the total transform of a fundamental point of f is connected and of dimension at least 1.

Examples

Zariski's main theorem for quasifinite morphisms

In EGA III, Grothendieck calls the following statement which does not involve connectedness a "Main theorem" of Zariski Grothendieck (1961, Théorème 4.4.3):

If f:X→Y is a quasi-projective morphism of Noetherian schemes then the set of points that are isolated in their fiber is open in X. Moreover the induced scheme of this set is isomorphic to an open subset of a scheme that is finite over Y.

In EGA IV, Grothendieck observed that the last statement could be deduced from a more general theorem about the structure of quasi-finite morphisms, and the latter is often referred to as the "Zariski's main theorem in the form of Grothendieck". It is well known that open immersions and finite morphisms are quasi-finite. Grothendieck proved that under the hypothesis of separatedness all quasi-finite morphisms are compositions of such Grothendieck (1966, Théorème 8.12.6):

if Y is a quasi-compact separated scheme and 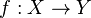f: X \to Y is a separated, quasi-finite, finitely presented morphism then there is a factorization into 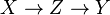X \to Z \to Y, where the first map is an open immersion and the second one is finite.

The relation between this theorem about quasi-finite morphisms and Théorème 4.4.3 of EGA III quoted above is that if f:X→Y is a projective morphism of varieties, then the set of points that are isolated in their fiber is quasifinite over Y. Then structure theorem for quasi-finite morphisms applies and yields the desired result.

Zariski's main theorem for commutative rings

Zariski (1949) reformulated his main theorem in terms of commutative algebra as a statement about local rings. Grothendieck (1961, Théorème 4.4.7) generalized Zariski's formulation as follows:

If B is an algebra of finite type over a local Noetherian ring A, and n is a maximal ideal of B which is minimal among ideals of B whose inverse image in A is the maximal ideal m of A, then there is a finite A-algebra A′ with a maximal ideal m′ (whose inverse image in A is m) such that the localization Bn is isomorphic to the A-algebra A′m′.

If in addition A and B are integral and have the same field of fractions, and A is integrally closed, then this theorem implies that A and B are equal. This is essentially Zariski's formulation of his main theorem in terms of commutative rings.

Zariski's main theorem: topological form

A topological version of Zariski's main theorem says that if x is a (closed) point of a normal complex variety it is unibranch; in other words there are arbitrarily small neighborhoods U of x such that the set of non-singular points of U is connected (Mumford 1999, III.9).

The property of being normal is stronger than the property of being unibranch: for example, a cusp of a plane curve is unibranch but not normal.

Zariski's main theorem: power series form

A formal power series version of Zariski's main theorem says that if x is a normal point of a variety then it is analytically normal; in other words the completion of the local ring at x is a normal integral domain (Mumford 1999, III.9).

See also

References

This article is issued from Wikipedia - version of the Wednesday, July 22, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.