Work stealing
In parallel computing, work stealing is a scheduling strategy for multithreaded computer programs. It solves the problem of executing a dynamically multithreaded computation, one that can "spawn" new threads of execution, on a statically multithreaded computer, with a fixed number of processors or (cores). It does so efficiently both in terms of execution time, memory usage, and inter-processor communication.
In a work stealing scheduler, each processor in a computer system has a queue of work items (computational tasks, threads) to perform. Each work item consists of a series of instructions, to be executed sequentially, but in the course of its execution, a work item may also spawn new work items that can feasibly be executed in parallel with its other work. These new items are initially put on the queue of the processor executing the work item. When a processor runs out of work, it looks at the queues of other processors and "steals" their work items. In effect, work stealing distributes the scheduling work over idle processors, and as long as all processors have work to do, no scheduling overhead occurs.[1]
Work stealing contrasts with work sharing, another popular scheduling approach for dynamic multithreading, where each work item is scheduled onto a processor when it is spawned. Compared to this approach, work stealing reduces the amount of process migration between processors, because no such migration occurs when all processors have work to do.[2]
The idea of work stealing goes back to the implementation of the Multilisp programming language and work on parallel functional programming languages in the 1980s.[2] It is employed in the scheduler for the Cilk programming language,[3] the Java fork/join framework,[4] and the .NET Task Parallel Library.[5]
Execution model
Work stealing is designed for a "strict" fork–join model of parallel computation, which means that a computation can be viewed as a directed acyclic graph with a single source (start of computation) and a single sink (end of computation). Each node in this graph represents either a fork or a join. Forks produce multiple logically parallel computations, variously called "threads"[2] or "strands".[6] Edges represent serial computation.[7][note 1]
As an example, consider the following trivial fork–join program in Cilk-like syntax:
function f(a, b):
c ← fork g(a)
d ← h(b)
join
return c + d
function g(a):
return a × 2
function h(a):
b ← fork g(a)
c ← a + 1
join
return b + c
The function call f(1, 2) gives rise to the following computation graph:
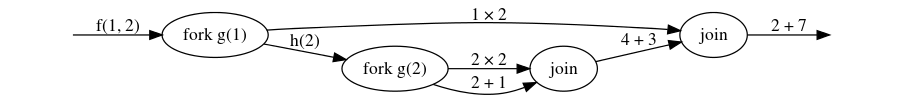
In the graph, when two edges leave a node, the computations represented by the edge labels are logically parallel: they may be performed either in parallel, or sequentially. The computation may only proceed past a join node when the computations represented by its incoming edges are complete. The work of a scheduler, now, is to assign the computations (edges) to processors in a way that makes the entire computation run to completion in the correct order (as constrained by the join nodes), preferably as fast as possible.
Algorithm
The randomized version of the work stealing algorithm presented by Blumofe and Leiserson maintains several threads of execution and schedules these onto  processors. Each of the processors has a double-ended queue (deque) of threads. Call the ends of the deque "top" and "bottom".
processors. Each of the processors has a double-ended queue (deque) of threads. Call the ends of the deque "top" and "bottom".
Each processor that has a current thread to execute, executes the instructions in the thread one by one, until it encounters an instruction that causes one of four "special" behaviors:[2]:10
- A spawn instruction causes a new thread to be created. The current thread is placed at the bottom of the deque, and the processor starts executing the new thread.
- A stalling instruction is one that temporarily halts execution of its thread. The processor pops a thread off the bottom of its deque and starts executing that thread. If its deque is empty, it starts work stealing, explained below.
- An instruction may cause a thread to die. The behavior in this case is the same as for an instruction that stalls.
- An instruction may enable another thread. The other thread is pushed onto the bottom of the deque, but the processor continues execution of its current thread.
Initially, a computation consists of a single thread and is assigned to some processor, while the other processors start off idle. Any processor that becomes idle starts the actual process of work stealing, which means the following:
- it picks another processor uniformly at random;
- if the other processor's deque is non-empty, it pops the top-most thread off the deque and starts executing that;
- else, repeat.
Child stealing vs. continuation stealing
Note that, in the rule for spawn, Blumofe and Leiserson suggest that the "parent" thread execute its new thread, as if performing a function call (in the C-like program f(x); g(y);, the function call to f completes before the call to g is performed). This is called "continuation stealing", because the continuation of the function can be stolen while the spawned thread is executed, and is the scheduling algorithm used in Cilk Plus.[6] It is not the only way to implement work stealing; the alternative strategy is called "child stealing" and is easier to implement as a library, without compiler support.[6] Child stealing is used by Threading Building Blocks, Microsoft's Task Parallel Library and OpenMP, although the latter gives the programmer control over which strategy is used.[6]
Efficiency
Several variants of work stealing have been proposed. The randomized variant due to Blumofe and Leiserson executes a parallel computation in expected time 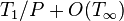 on
on  processors; here,
processors; here,  is the work, or the amount of time required to run the computation on a serial computer, and
is the work, or the amount of time required to run the computation on a serial computer, and 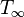 is the span, the amount of time required on an infinitely parallel machine.[note 2] This means that, in expectation, the time required is at most a constant factor times the theoretical minimum.[2] However, the running time (in particular, the number of steals executed) can be exponential in
is the span, the amount of time required on an infinitely parallel machine.[note 2] This means that, in expectation, the time required is at most a constant factor times the theoretical minimum.[2] However, the running time (in particular, the number of steals executed) can be exponential in 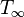 in the worst case.[8] A localized variant, in which a processor attempts to steal back its own work whenever it is free, has also been analyzed theoretically and practically.[9][10]
in the worst case.[8] A localized variant, in which a processor attempts to steal back its own work whenever it is free, has also been analyzed theoretically and practically.[9][10]
Space usage
A computation scheduled by the Blumofe–Leiserson version of work stealing uses 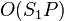 stack space, if
stack space, if  were the stack usage of the same computation on a single processor,[2] fitting the authors' own earlier definition of space efficiency.[11] This bound requires continuation stealing; in a child stealing scheduler, it does not hold, as can be seen from the following example:[6]
were the stack usage of the same computation on a single processor,[2] fitting the authors' own earlier definition of space efficiency.[11] This bound requires continuation stealing; in a child stealing scheduler, it does not hold, as can be seen from the following example:[6]
for i = 0 to n:
fork f(i)
join
In a child-stealing implementation, all "forked" calls to f are put in a work queue that thus grows to size n, which can be made arbitrarily large.
Multiprogramming variant
The work stealing algorithm as outlined earlier, and its analysis, assume a computing environment where a computation is scheduled onto a set of dedicated processors. In a multiprogramming (multi-tasking) environment, the algorithm must be modified to instead schedule computation tasks onto a pool of worker threads, which in turn are scheduled onto the actual processors by an operating system scheduler. At any given time, the OS scheduler will assign to the work stealing process some number PA ≤ P of the P processors in the computer, because other processes may be using the remaining processors. In this setting, work stealing with a pool of P worker threads has the problem that workers acting as thieves may cause livelock: they may block the execution of workers that would actually spawn useful tasks.[12][13]
A variant of work stealing has been devised for this situation, which executes a computation in expected time
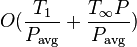 ,
,
where Pavg is the average number of processors allocated to the computation by the OS scheduler over the computation's running time.[14] The multiprogramming work-scheduler scheduler differs from the traditional version in two respects:
- Its queues are non-blocking. While on dedicated processors, access to the queues can be synchronized using locks, this is not advisable in a multiprogramming environment since the operating system might preempt the worker thread holding the lock, blocking the progress of any other workers that try to access the same queue.
- Before each attempt to steal work, a worker thread calls a "yield" system call that yields the processor on which it is scheduled to the OS, in order to prevent starvation.
Attempts to improve on the multiprogramming work stealer have focused on cache locality issues[10] and improved queue data structures.[15]
Alternatives
Several scheduling algorithms for dynamically multithreaded computations compete with work stealing. Besides the traditional work sharing approach, there is a scheduler called parallel depth-first (PDF) that improves on the space bounds of work stealing,[16] as well giving better performance in some situations where the cores of a chip multiprocessor share a cache.[1]
Notes
- ↑ In the original presentation, serial computations were represented as nodes as well, and a directed edge represented the relation "is followed by".
- ↑ See analysis of parallel algorithms for definitions.
References
- 1 2 Chen, Shimin; Gibbons, Phillip B.; Kozuch, Michael; Liaskovitis, Vasileios; Ailamaki, Anastassia; Blelloch, Guy E.; Falsafi, Babak; Fix, Limor; Hardavellas, Nikos; Mowry, Todd C.; Wilkerson, Chris (2007). Scheduling threads for constructive cache sharing on CMPs (PDF). Proc. ACM Symp. on Parallel Algorithms and Architectures. pp. 105–115.
- 1 2 3 4 5 6 Blumofe, Robert D.; Leiserson, Charles E. (1999). "Scheduling multithreaded computations by work stealing" (PDF). JACM 46 (5): 720–748. doi:10.1145/324133.324234.
- ↑ Blumofe, Robert D.; Joerg, Christopher F.; Kuszmaul, Bradley C.; Leiserson, Charles E.; Randall, Keith H.; Zhou, Yuli (1996). "Cilk: An efficient multithreaded runtime system". J. Parallel and Distributed Computing 37 (1): 55–69. doi:10.1006/jpdc.1996.0107.
- ↑ Doug Lea (2000). A Java fork/join framework (PDF). ACM Conf. on Java.
- ↑ Leijen, Daan; Schulte, Wolfram; Burckhardt, Sebastian (2009). "The Design of a Task Parallel Library". ACM SIGPLAN Notices 44 (10). doi:10.1145/1639949.1640106.
- 1 2 3 4 5 Robison, Arch (15 January 2014). A Primer on Scheduling Fork–Join Parallelism with Work Stealing (PDF) (Technical report). ISO/IEC JTC 1/SC 22/WG 21—The C++ Standards Committee. N3872.
- ↑ Halpern, Pablo (24 September 2012). Strict Fork–Join Parallelism (PDF) (Technical report). ISO/IEC JTC 1/SC 22/WG 21—The C++ Standards Committee. N3409=12-0099.
- ↑ Leiserson, Charles E.; Schardl, Tao B.; Suksompong, Warut (2016). "Upper Bounds on Number of Steals in Rooted Trees". Theory of Computing Systems 58 (2): 223–240. doi:10.1007/s00224-015-9613-9.
- ↑ Suksompong, Warut; Leiserson, Charles E.; Schardl, Tao B. (2016). "On the efficiency of localized work stealing". Information Processing Letters 116 (2): 100–106. doi:10.1016/j.ipl.2015.10.002.
- 1 2 Acar, Umut A.; Blelloch, Guy E.; Blumofe, Robert D. "The Data Locality of Work Stealing" (PDF). Theory of Computing Systems 35 (3): 321–347. doi:10.1007/s00224-002-1057-3.
- ↑ Blumofe, Robert D.; Leiserson, Charles E. (1998). "Space-efficient scheduling of multithreaded computations". SIAM J. Computing 27 (1): 202–229. doi:10.1137/s0097539793259471.
- ↑ Ding, Xiaoning; Wang, Kaibo; Gibbons, Phillip B.; Zhang, Xiaodong (2012). BWS: Balanced Work Stealing for Time-Sharing Multicores (PDF). EuroSys.
- ↑ Blumofe, Robert D.; Papadopoulos, Dionisios (1998). The Performance of Work Stealing in Multiprogrammed Environments (Technical report). University of Texas at Austin, Department of Computer Sciences. CiteSeerX: 10
.1 ..1 .48 .2247 - ↑ Arora, Nimar S.; Blumofe, Robert D.; Plaxton, C. Greg (2001). "Thread scheduling for multiprogrammed multiprocessors" (PDF). Theory of Computing Systems 34 (2): 115–144. doi:10.1007/s002240011004.
- ↑ Chase, David R.; Lev, Yosef (2005). Dynamic Circular Work-Stealing Deque. ACM Symp. on Parallelism in Algorithms and Architectures. CiteSeerX: 10
.1 ..1 .170 .1097 - ↑ Blelloch, Guy E.; Gibbons, Phillip B.; Matias, Yossi (1999). "Provably efficient scheduling for languages with fine-grained parallelism" (PDF). Journal of the ACM 46 (2): 281–321. doi:10.1145/301970.301974.