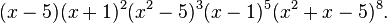Wong graph
| Wong graph | |
|---|---|
| Named after | Pak-Ken Wong |
| Vertices | 30 |
| Edges | 75 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 5 |
| Automorphisms | 96 |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Properties | Cage |
In the mathematical field of graph theory, the Wong graph is a 5-regular undirected graph with 30 vertices and 75 edges.[1][2] It is one of the four (5,5)-cage graphs, the others being the Foster cage, the Meringer graph, and the Robertson–Wegner graph.
Like the unrelated Harries–Wong graph, it is named after Pak-Ken Wong.[3]
It has chromatic number 4, diameter 3, and is 5-vertex-connected.
Algebraic properties
The characteristic polynomial of the Wong graph is
References
- ↑ Weisstein, Eric W., "Wong Graph", MathWorld.
- ↑ Meringer, Markus (1999), "Fast generation of regular graphs and construction of cages", Journal of Graph Theory 30 (2): 137–146, doi:10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G, MR 1665972.
- ↑ Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982.
This article is issued from Wikipedia - version of the Friday, January 29, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.