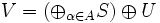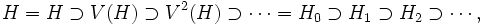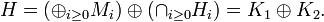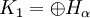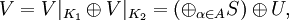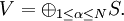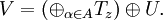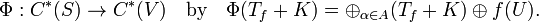Wold's decomposition

This article is about the general mathematical result. For the application to time series analysis, see Wold's theorem.

In mathematics, particularly in operator theory, Wold decomposition or Wold–von Neumann decomposition, named after Herman Wold and John von Neumann, is a classification theorem for isometric linear operators on a given Hilbert space. It states that every isometry is a direct sum of copies of the unilateral shift and a unitary operator.

In time series analysis, the theorem implies that any stationary discrete-time stochastic process can be decomposed into a pair of uncorrelated processes, one deterministic, and the other being a moving average process.

Details

Let H be a Hilbert space, L(H) be the bounded operators on H, and V ∈ L(H) be an isometry. The Wold decomposition states that every isometry V takes the form

V = (\oplus_{\alpha \in A} S) \oplus U

for some index set A, where S in the unilateral shift on a Hilbert space H_α, and U is a unitary operator (possible vacuous). The family {H_α} consists of isomorphic Hilbert spaces.

A proof can be sketched as follows. Successive applications of V give a descending sequences of copies of H isomorphically embedded in itself:

H = H \supset V(H) \supset V^2 (H) \supset \cdots = H_0 \supset H_1 \supset H_2 \supset \cdots,

where V(H) denotes the range of V. The above defined H_i = Vⁱ(H). If one defines

M_i = H_i \ominus H_{i+1} = V^i (H \ominus V(H)) \quad \text{for} \quad i \geq 0 \;,

then

H = (\oplus_{i \geq 0} M_i) \oplus (\cap_{i \geq 0} H_i) = K_1 \oplus K_2.

It is clear that K₁ and K₂ are invariant subspaces of V.

So V(K₂) = K₂. In other words, V restricted to K₂ is a surjective isometry, i.e., a unitary operator U.

Furthermore, each M_i is isomorphic to another, with V being an isomorphism between M_i and M_i+1: V "shifts" M_i to M_i+1. Suppose the dimension of each M_i is some cardinal number α. We see that K₁ can be written as a direct sum Hilbert spaces

K_1 = \oplus H_{\alpha}

where each H_α is an invariant subspaces of V and V restricted to each H_α is the unilateral shift S. Therefore

V = V \vert_{K_1} \oplus V\vert_{K_2} = (\oplus_{\alpha \in A} S) \oplus U,

which is a Wold decomposition of V.

Remarks

It is immediate from the Wold decomposition that the spectrum of any proper, i.e. non-unitary, isometry is the unit disk in the complex plane.

An isometry V is said to be pure if, in the notation of the above proof, ∩_i≥0 H_i = {0}. The multiplicity of a pure isometry V is the dimension of the kernel of V*, i.e. the cardinality of the index set A in the Wold decomposition of V. In other words, a pure isometry of multiplicity N takes the form

V = \oplus_{1 \le \alpha \le N} S .

In this terminology, the Wold decomposition expresses an isometry as a direct sum of a pure isometry and a unitary operator.

A subspace M is called a wandering subspace of V if Vⁿ(M) ⊥ V^m(M) for all n ≠ m. In particular, each M_i defined above is a wandering subspace of V.

A sequence of isometries

The decomposition above can be generalized slightly to a sequence of isometries, indexed by the integers.

The C*-algebra generated by an isometry

Consider an isometry V ∈ L(H). Denote by C*(V) the C*-algebra generated by V, i.e. C*(V) is the norm closure of polynomials in V and V*. The Wold decomposition can be applied to characterize C*(V).

Let C(T) be the continuous functions on the unit circle T. We recall that the C*-algebra C*(S) generated by the unilateral shift S takes the following form

C*(S) = {T_f + K | T_f is a Toeplitz operator with continuous symbol f ∈ C(T) and K is a compact operator}.

In this identification, S = T_z where z is the identity function in C(T). The algebra C*(S) is called the Toeplitz algebra.

Theorem (Coburn) C*(V) is isomorphic to the Toeplitz algebra and V is the isomorphic image of T_z.

The proof hinges on the connections with C(T), in the description of the Toeplitz algebra and that the spectrum of an unitary operator is contained in the circle T.

The following properties of the Toeplitz algebra will be needed:

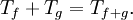
$T_f + T_g = T_{f+g}.\,$
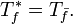
$T_f ^* = T_{{\bar f}} .$
The semicommutator 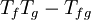$T_fT_g - T_{fg} \,$ is compact.

The Wold decomposition says that V is the direct sum of copies of T_z and then some unitary U:

V = (\oplus_{\alpha \in A} T_z) \oplus U.

So we invoke the continuous functional calculus f → f(U), and define

\Phi : C^*(S) \rightarrow C^*(V) \quad \text{by} \quad \Phi(T_f + K) = \oplus_{\alpha \in A} (T_f + K) \oplus f(U).

One can now verify Φ is an isomorphism that maps the unilateral shift to V:

By property 1 above, Φ is linear. The map Φ is injective because T_f is not compact for any non-zero f ∈ C(T) and thus T_f + K = 0 implies f = 0. Since the range of Φ is a C*-algebra, Φ is surjective by the minimality of C*(V). Property 2 and the continuous functional calculus ensure that Φ preserves the *-operation. Finally, the semicommutator property shows that Φ is multiplicative. Therefore the theorem holds.

References

Coburn, L. (1967). "The C*-algebra of an isometry". Bull. Amer. Math. Soc. 73 (5): 722–726. doi:10.1090/S0002-9904-1967-11845-7.
Constantinescu, T. (1996). Schur Parameters, Factorization and Dilation Problems. Operator Theory, Advances and Applications 82. Birkhäuser. ISBN 3-7643-5285-X.
Douglas, R. G. (1972). Banach Algebra Techniques in Operator Theory. Academic Press. ISBN 0-12-221350-5.
Rosenblum, Marvin; Rovnyak, James (1985). Hardy Classes and Operator Theory. Oxford University Press. ISBN 0-19-503591-7.

This article is issued from Wikipedia - version of the Tuesday, February 09, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.