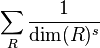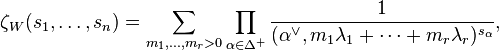Witten zeta function

In mathematics, the Witten zeta function, introduced by Witten (1991), is a function associated to a root system that encodes the degrees of the irreducible representations of the corresponding Lie group. It is a special case of the Shintani zeta function.

Definition

Witten's original definition of the zeta function of a semisimple Lie group was

\sum_R\frac{1}{\dim(R)^s}

where the sum is over equivalence classes of irreducible representations R.

If Δ of rank r is a root system with n positive roots in Δ⁺ and with simple roots λ_i, the Witten zeta function of several variables is given by

\zeta_W(s_1,\dots,s_n) = \sum_{m_1,\dots,m_r>0}\prod_{\alpha\in \Delta^+}\frac{1}{(\alpha^\or, m_1\lambda_1+\cdots+m_r\lambda_r)^{s_\alpha}},

The original zeta function studied by Witten differed from this slightly, in that all the numbers s_α are equal, and the function is multiplied by a constant.

References

Witten, Edward (1991), "On quantum gauge theories in two dimensions", Communications in Mathematical Physics 141 (1): 153–209, doi:10.1007/bf02100009, ISSN 0010-3616, MR 1133264, Zbl 0762.53063
Zagier, Don (1994), "Values of zeta functions and their applications", First European Congress of Mathematics, Vol. II (Paris, 1992), Progr. Math. 120, Basel, Boston, Berlin: Birkhäuser, pp. 497–512, MR 1341859, Zbl 0822.11001

This article is issued from Wikipedia - version of the Wednesday, September 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.