Witt vector
In mathematics, a Witt vector is an infinite sequence of elements of a commutative ring. Ernst Witt showed how to put a ring structure on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.
Motivation
Any  -adic integer (an element of
-adic integer (an element of 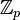 ) can be written as a power series
) can be written as a power series
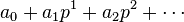 , where the
, where the  's are usually taken from the set
's are usually taken from the set 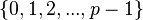 . However, it is hard to figure out an algebraic expression for addition and multiplication, as one faces the problem of carrying. Luckily, this set of representatives is not the only possible choice, and Teichmüller suggested an alternative set consisting of 0 together with the
. However, it is hard to figure out an algebraic expression for addition and multiplication, as one faces the problem of carrying. Luckily, this set of representatives is not the only possible choice, and Teichmüller suggested an alternative set consisting of 0 together with the 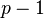 st roots of
st roots of 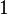 : in other words, the
: in other words, the  roots of
roots of
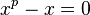 in
in 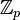 .
.
These Teichmüller representatives can be identified with the elements of the finite field 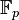 of order
of order  (by taking residues modulo
(by taking residues modulo  ), and elements of
), and elements of 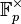 are taken to their representatives by the Teichmüller character
are taken to their representatives by the Teichmüller character 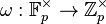 . This identifies the set of
. This identifies the set of  -adic integers with infinite sequences of elements of
-adic integers with infinite sequences of elements of 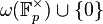 .
.
We now have the following problem: given two infinite sequences of elements of 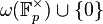 , describe their sum and product as
, describe their sum and product as  -adic integers explicitly. This problem was solved by Witt using Witt vectors.
-adic integers explicitly. This problem was solved by Witt using Witt vectors.
Details
We basically want to derive the ring  -adic integers
-adic integers 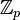 from the finite field with
from the finite field with  elements,
elements, 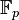 , by some general construction.
, by some general construction.
The ring  of
of  -adic integers consists of the sequences
-adic integers consists of the sequences 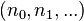 with
with 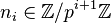 ,such that
,such that 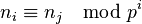 if
if  . (It is a projective limit.) Its elements can be expanded as (formal) power series
. (It is a projective limit.) Its elements can be expanded as (formal) power series 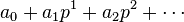 in
in  , where the
, where the  's are usually taken from the set
's are usually taken from the set 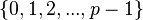 . (The power series usually do not converge in
. (The power series usually do not converge in 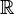 , but do converge in
, but do converge in 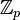 , with
, with  and
and 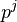 being identified with their images under
being identified with their images under 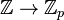 .) Set-theoretically,
.) Set-theoretically,  is just
is just 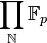 ; but the two sets are not isomorphic as rings. If we denote
; but the two sets are not isomorphic as rings. If we denote  by
by  , then the addition should instead be:
, then the addition should instead be:
But we lack some properties of the coefficients to produce a general formula.
Luckily, there is an alternative subset of 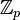 which can work as the coefficient set. This is the set of Teichmüller representatives of elements of
which can work as the coefficient set. This is the set of Teichmüller representatives of elements of 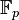 . Without
. Without  they form a subgroup of
they form a subgroup of 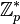 , identified with
, identified with 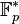 through the Teichmüller character
through the Teichmüller character 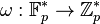 . Note that
. Note that 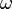 is not additive, as the sum need not be a representative. Despite this, if
is not additive, as the sum need not be a representative. Despite this, if 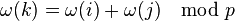 in
in 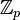 , then
, then 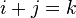 in
in 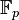 . This is conceptually justified by
. This is conceptually justified by 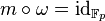 if we denote
if we denote 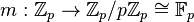 .
.
Teichmüller representatives are explicitly calculated as roots of 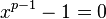 through Hensel lifting. For example, in
through Hensel lifting. For example, in 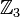 , to calculate the representative of
, to calculate the representative of 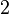 , you first find the unique solution of
, you first find the unique solution of 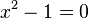 in
in 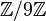 with
with  ; you get
; you get 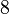 , then repeat it in
, then repeat it in 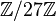 , with conditions
, with conditions 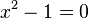 and
and  ; this time it is
; this time it is 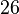 , and so on. The existence of lift in each step is guaranteed by
, and so on. The existence of lift in each step is guaranteed by 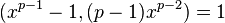 in every
in every 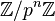 .
.
We can also write the representatives as 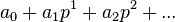 . Note for every
. Note for every 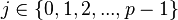 , there is exactly one representative, namely
, there is exactly one representative, namely 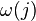 , with
, with 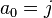 , so we can also expand every
, so we can also expand every  -adic integer as a power series in
-adic integer as a power series in  , with coefficients from the Teichmüller representatives.
, with coefficients from the Teichmüller representatives.
Explicitly, if 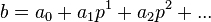 , then
, then 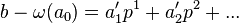 . Then you subtract
. Then you subtract 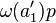 and proceed similarly. Note the coefficients you get most probably differ from the
and proceed similarly. Note the coefficients you get most probably differ from the  's modulo
's modulo  , except the first one.
, except the first one.
This time we have additional properties of the coefficients like  , so we can make some changes to get a neat formula. Since the Teichmüller character is not additive, we don't have
, so we can make some changes to get a neat formula. Since the Teichmüller character is not additive, we don't have 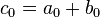 in
in 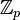 . But it happens in
. But it happens in 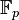 , as the first congruence implies. So actually
, as the first congruence implies. So actually 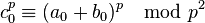 , thus
, thus 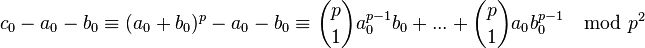 . Since
. Since 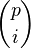 is divisible by
is divisible by  , this resolves the
, this resolves the  -coefficient problem of
-coefficient problem of 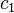 and gives
and gives 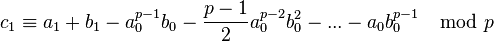 . Note this completely determines
. Note this completely determines 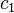 by the lift. Moreover, the
by the lift. Moreover, the 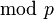 indicates that the calculation can actually be done in
indicates that the calculation can actually be done in 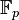 , satisfying our basic aim.
, satisfying our basic aim.
Now for 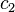 . It is already very cumbersome at this step.
. It is already very cumbersome at this step. 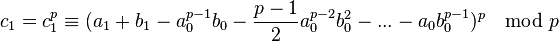 . As for
. As for  , a single
, a single  th power is not enough: actually we take
th power is not enough: actually we take 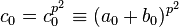 .
. 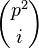 is not always divisible by
is not always divisible by  , but that only happens when
, but that only happens when 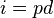 , in which case
, in which case  combined with similar monomials in
combined with similar monomials in 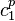 would make a multiple of
would make a multiple of  .
.
At this step, we see that we are actually working with something like
This motivates the definition of Witt vectors.
Construction of Witt rings
Fix a prime number p. A Witt vector over a commutative ring R is a sequence :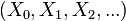 of elements of R. Define the Witt polynomials
of elements of R. Define the Witt polynomials  by
by
and in general
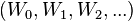 is called the ghost components of the Witt vector
is called the ghost components of the Witt vector 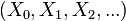 , and is usually denoted by
, and is usually denoted by 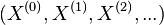 .
.
Then Witt showed that there is a unique way to make the set of Witt vectors over any commutative ring R into a ring, called the ring of Witt vectors, such that
- the sum and product are given by polynomials with integral coefficients that do not depend on R, and
- Every Witt polynomial is a homomorphism from the ring of Witt vectors over R to R.
In other words, if
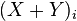 and
and 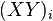 are given by polynomials with integral coefficients that do not depend on R, and
are given by polynomials with integral coefficients that do not depend on R, and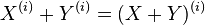 ,
, 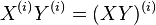 .
.
The first few polynomials giving the sum and product of Witt vectors can be written down explicitly. For example,
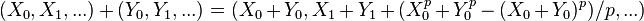
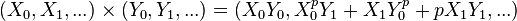 .
.
Examples
- The Witt ring of any commutative ring R in which p is invertible is just isomorphic to RN (the product of a countable number of copies of R). In fact the Witt polynomials always give a homomorphism from the ring of Witt vectors to RN, and if p is invertible this homomorphism is an isomorphism.
- The Witt ring of the finite field of order p is the ring of p-adic integers, as is demonstrated above.
- The Witt ring of a finite field of order pn is the unramified extension of degree n of the ring of p-adic integers.
Universal Witt vectors
The Witt polynomials for different primes p are special cases of universal Witt polynomials, which can be used to form a universal Witt ring (not depending on a choice of prime p). Define the universal Witt polynomials Wn for n≥1 by
and in general
Again, 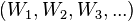 is called the ghost components of the Witt vector
is called the ghost components of the Witt vector 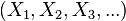 , and is usually denoted by
, and is usually denoted by 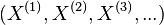 .
.
We can use these polynomials to define the ring of universal Witt vectors over any commutative ring R in much the same way as above (so the universal Witt polynomials are all homomorphisms to the ring R).
Generating Functions
Later Witt orally stated another approach using generating functions.[1]
Definition
Let  be a Witt vector and define
be a Witt vector and define
For  let
let 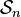 denote the collection of subsets of
denote the collection of subsets of 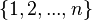 whose elements add up to
whose elements add up to  . Then
. Then 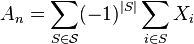 .
.
We can get the ghost components by taking the logarithmic derivative:
Sum
Now we can see 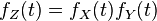 if
if 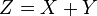 . So that
. So that 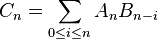 if
if 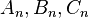 are respective coefficients in the power series for
are respective coefficients in the power series for 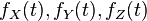 . Then
. Then 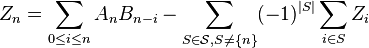 . Since
. Since  is a polynomial in
is a polynomial in  and likely for
and likely for  , we can show by induction that
, we can show by induction that 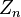 is a polynomial in
is a polynomial in 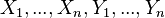 .
.
Product
If we set 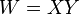 then
then
But
Now 3-tuples 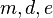 with
with 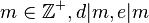 are in bijection with 3-tuples
are in bijection with 3-tuples 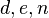 with
with 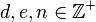 , via
, via ![n=m/[d,e]](../I/m/90dddc21b70efa2ee4cd31803df24815.png) (
(![[d,e]](../I/m/a816f62cb0a168ad080e1c927399060f.png) is the Least common multiple), our series becomes
is the Least common multiple), our series becomes
So that
where 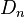 s are polynomials of
s are polynomials of 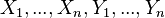 . So by similar induction, suppose
. So by similar induction, suppose 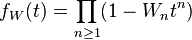 , then
, then  can be solved as polynomials of
can be solved as polynomials of 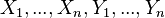 .
.
Ring schemes
The map taking a commutative ring R to the ring of Witt vectors over R (for a fixed prime p) is a functor from commutative rings to commutative rings, and is also representable, so it can be thought of as a ring scheme, called the Witt scheme, over Spec(Z). The Witt scheme can be canonically identified with the spectrum of the ring of symmetric functions.
Similarly the rings of truncated Witt vectors, and the rings of universal Witt vectors, correspond to ring schemes, called the truncated Witt schemes and the universal Witt scheme.
Moreover, the functor taking the commutative ring  to the set
to the set  is represented by the affine space
is represented by the affine space 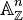 , and the ring structure on Rn makes
, and the ring structure on Rn makes 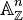 into a ring scheme denoted
into a ring scheme denoted 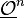 . From the construction of truncated Witt vectors it follows that their associated ring scheme
. From the construction of truncated Witt vectors it follows that their associated ring scheme 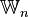 is the scheme
is the scheme 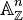 with the unique ring structure such that the morphism
with the unique ring structure such that the morphism 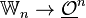 given by the Witt polynomials is a morphism of ring schemes.
given by the Witt polynomials is a morphism of ring schemes.
Commutative unipotent algebraic groups
Over an algebraically closed field of characteristic 0, any unipotent abelian connected algebraic group is isomorphic to a product of copies of the additive group 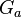 .
The analogue of this for fields of characteristic p is false: the truncated Witt schemes are counterexamples. (We make them into algebraic groups by forgetting the multiplication and just using the additive structure.) However these are essentially the only counterexamples: over an algebraically closed field of characteristic p, any unipotent abelian connected algebraic group is
isogenous to a product of truncated Witt group schemes.
.
The analogue of this for fields of characteristic p is false: the truncated Witt schemes are counterexamples. (We make them into algebraic groups by forgetting the multiplication and just using the additive structure.) However these are essentially the only counterexamples: over an algebraically closed field of characteristic p, any unipotent abelian connected algebraic group is
isogenous to a product of truncated Witt group schemes.
See also
References
- Dolgachev, I.V. (2001), "Witt vector", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel (2009), "Witt vectors. I.", Handbook of algebra. Vol. 6, Amsterdam: Elsevier/North-Holland, pp. 319–472, arXiv:0804.3888, ISBN 978-0-444-53257-2, MR 2553661
- Mumford, David, Lectures on Curves on an Algebraic Surface, Annals of Mathematics Studies 59, Princeton, NJ: Princeton University Press, ISBN 978-0-691-07993-6
- Serre, Jean-Pierre (1979), Local fields, Graduate Texts in Mathematics 67, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90424-5, MR 554237, section II.6
- Serre, Jean-Pierre (1988), Algebraic groups and class fields, Graduate Texts in Mathematics 117, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96648-9, MR 918564
- Witt, Ernst (1936), "Zyklische Körper und Algebren der Characteristik p vom Grad pn. Struktur diskret bewerteter perfekter Körper mit vollkommenem Restklassenkörper der Charakteristik pn", Journal für Reine und Angewandte Mathematik (in German) 176: 126–140, doi:10.1515/crll.1937.176.126
- Greenberg, M. J. (1969), Lectures on Forms in Many Variables, New York and Amsterdam, Benjamin, MR 241358, ASIN: B0006BX17M
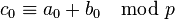
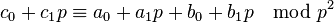
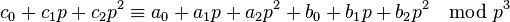
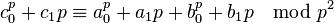
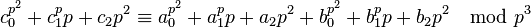
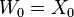
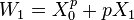
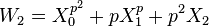
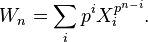
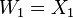
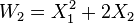
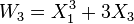
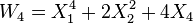
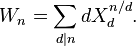
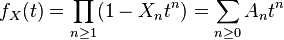
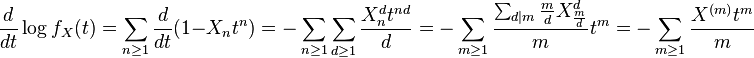
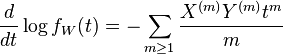
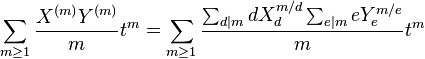
![\sum_{d,e\ge 1}\frac{\frac{d e}{ [d,e]}\sum_{n\ge 1} (X_d^{ [d,e]/d } Y_e^{ [d,e]/e } t^{ [d,e] })^n}{n}](../I/m/d8716083fd3e7b6d600670490c5043d4.png)
![f_W(t)=\prod_{d,e\ge 1}(1-X_d^{[d,e]/d}Y_e^{[d,e]/e} t^{[d,e]})^{d e/[d,e]}=\sum_{n\ge 0}D_n t^n](../I/m/18ade3b58f41fe9f3b18b08bb92fefa3.png)