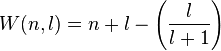Wiswesser's rule

The Wiswesser rule gives a simple method to determine the energetic sequence of the atomic subshells . n is the principal quantum number and l is the azimuthal quantum number. The energetic sequence of the subshells characterized by the quantum numbers is the sequence that leads to a monotonous increasing row of function values for the Wiswesser-function.

For example: if 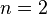and 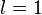, this correspondents with an 2p-orbital.

If the results of this function for each shell and subshell are ordered, the resulting sequence is: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p...

To illustrate this, the corresponding values of each of these shells can be found in the table below:

Order in which orbitals are arranged by increasing energy according to the Madelung rule. Each diagonal red arrow corresponds to a different value of n + ℓ.

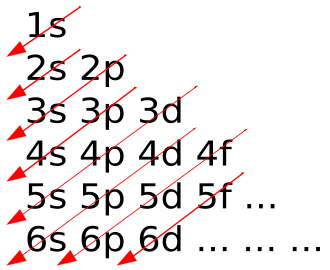
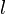2	1	2.5
2	2	3.33
3	1	3.5
3	2	4.33
4	1	4.5
3	3	5.25
4	2	5.33
5	1	5.5
4	3	6.25
5	2	6.33
6	1	6.5
4	4	7.2
5	3	7.25
6	2	7.33
7	1	7.5
5	4	8.2
6	3	8.25
7	2	8.33

We can now clearly see that the Aufbau principle and Wiswesser's Rule come to the same order of filling electron shells.

See also

• Atomic orbital energy
• Aufbau principle
• Electron configuration

References