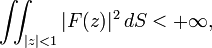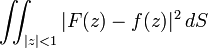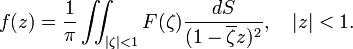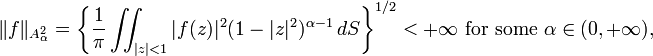Wirtinger's representation and projection theorem

In mathematics, Wirtinger's representation and projection theorem is a theorem proved by Wilhelm Wirtinger in 1932 in connection with some problems of approximation theory. This theorem gives the representation formula for the holomorphic subspace 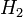$\left.\right. H_2$ of the simple, unweighted holomorphic Hilbert space 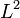$\left.\right. L^2$ of functions square-integrable over the surface of the unit disc 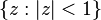$\left.\right.\{z:|z|<1\}$ of the complex plane, along with a form of the orthogonal projection from 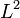$\left.\right. 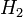L^2$ to $\left.\right. H_2$ .

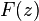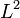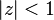Wirtinger's paper ^[1] contains the following theorem presented also in Joseph L. Walsh's well-known monograph ^[2] (p. 150) with a different proof. If $\left.\right.\left. F(z)\right.$ is of the class $\left.\right. L^2$ on $\left.\right. |z|<1$ , i.e.

\iint_{|z|<1}|F(z)|^2 \, dS<+\infty,

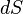where $\left.\right. dS$ is the area element, then the unique function 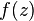$\left.\right. f(z)$ of the holomorphic subclass 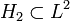$H_2\subset L^2$ , such that

\iint_{|z|<1}|F(z)-f(z)|^2 \, dS

is least, is given by

f(z)=\frac1\pi\iint_{|\zeta|<1}F(\zeta)\frac{dS}{(1-\overline\zeta z)^2},\quad |z|<1.

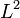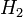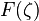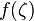The last formula gives a form for the orthogonal projection from $\left.\right. L^2$ to $\left.\right. H_2$ . Besides, replacement of $\left.\right. F(\zeta)$ by $\left.\right. f(\zeta)$ makes it Wirtinger's representation for all 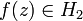$f(z)\in H_2$ . This is an analog of the well-known Cauchy integral formula with the square of the Cauchy kernel. Later, after the 1950s, a degree of the Cauchy kernel was called reproducing kernel, and the notation 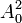$\left.\right. 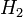A^2_0$ became common for the class $\left.\right. H_2$ .

In 1948 Mkhitar Djrbashian^[3] extended Wirtinger's representation and projection to the wider, weighted Hilbert spaces 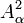$\left.\right. A^2_\alpha$ of functions 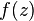$\left.\right. f(z)$ holomorphic in 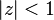$\left.\right.|z|<1$ , which satisfy the condition

\|f\|_{A^2_\alpha}=\left\{\frac1\pi\iint_{|z|<1}|f(z)|^2(1-|z|^2)^{\alpha-1} \, dS\right\}^{1/2}<+\infty\text{ for some }\alpha\in(0,+\infty),

and also to some Hilbert spaces of entire functions. The extensions of these results to some weighted 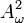$\left.\right. A^2_\omega$ spaces of functions holomorphic in 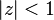$\left.\right. |z|<1$ and similar spaces of entire functions, the unions of which respectively coincide with all functions holomorphic in 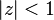$\left.\right. |z|<1$ and the whole set of entire functions can be seen in.^[4]

References

↑ Wirtinger, W. (1932). "Uber eine Minimumaufgabe im Gebiet der analytischen Functionen". Monatshefte fur Math. und Phys. 39: 377–384. doi:10.1007/bf01699078.
↑ Walsh, J. L. (1956). "Interpolation and Approximation by Rational Functions in the Complex Domain". Amer. Math. Soc. Coll. Publ. XX (Ann Arbor, Michigan: Edwards Brothers, Inc.).
↑ Djrbashian, M. M. (1948). "On the Representability Problem of Analytic Functions" (PDF). Soobsch. Inst. Matem. i Mekh. Akad. Nauk Arm. SSR 2: 3–40.
↑ Jerbashian, A. M. (2005). "On the Theory of Weighted Classes of Area Integrable Regular Functions". Complex Variables 50: 155–183. doi:10.1080/02781070500032846.

This article is issued from Wikipedia - version of the Wednesday, February 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Wirtinger's representation and projection theorem

See also

References