Wilson prime
| Named after | John Wilson |
|---|---|
| Publication year | 1938[1] |
| Author of publication | Emma Lehmer |
| Number of known terms | 3 |
| First terms | 5, 13, 563 |
| Largest known term | 563 |
| OEIS index | A007540 |
A Wilson prime, named after English mathematician John Wilson, is a prime number p such that p2 divides (p − 1)! + 1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides (p − 1)! + 1.
The only known Wilson primes are 5, 13, and 563 (sequence A007540 in OEIS); if any others exist, they must be greater than 2×1013.[2] It has been conjectured that infinitely many Wilson primes exist, and that the number of Wilson primes in an interval [x, y] is about log(log(y)/log(x)).[3]
Several computer searches have been done in the hope of finding new Wilson primes.[4][5][6] The Ibercivis distributed computing project includes a search for Wilson primes.[7] Another search is coordinated at the mersenneforum.[8]
Generalizations
Wilson primes of order n
Wilson's theorem can be expressed in general as 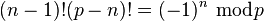 for every prime
for every prime 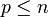 . Generalized Wilson primes of order n are the primes p such that
. Generalized Wilson primes of order n are the primes p such that  divides
divides 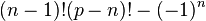 .
.
It was conjectured that for every natural number n, there are infinitely many Wilson primes of order n.
 |
prime 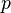 such that such that  divides divides 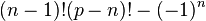 |
OEIS sequence |
|---|---|---|
| 1 | 5, 13, 563, ... | A007540 |
| 2 | 2, 3, 11, 107, 4931, ... | A079853 |
| 3 | 7, ... | |
| 4 | 10429, ... | |
| 5 | 5, 7, 47, ... | |
| 6 | 11, ... | |
| 7 | 17, ... | |
| 8 | ... | |
| 9 | 541, ... | |
| 10 | 11, 1109, ... | |
| 11 | 17, 2713, ... | |
| 12 | ... | |
| 13 | 13, ... | |
| 14 | ... | |
| 15 | 349, ... | |
| 16 | 31, ... | |
| 17 | 61, 251, 479, ... | A152413 |
| 18 | 13151527, ... | |
| 19 | 71, ... | |
| 20 | 59, 499, ... | |
| 21 | 217369, ... | |
| 22 | ... | |
| 23 | ... | |
| 24 | 47, 3163, ... | |
| 25 | ... | |
| 26 | 97579, ... | |
| 27 | 53, ... | |
| 28 | 347, ... | |
| 29 | ... | |
| 30 | 137, 1109, 5179, ... |
Least generalized Wilson prime of order n are
Near-Wilson primes
| p | B |
|---|---|
| 1282279 | +20 |
| 1306817 | −30 |
| 1308491 | −55 |
| 1433813 | −32 |
| 1638347 | −45 |
| 1640147 | −88 |
| 1647931 | +14 |
| 1666403 | +99 |
| 1750901 | +34 |
| 1851953 | −50 |
| 2031053 | −18 |
| 2278343 | +21 |
| 2313083 | +15 |
| 2695933 | −73 |
| 3640753 | +69 |
| 3677071 | −32 |
| 3764437 | −99 |
| 3958621 | +75 |
| 5062469 | +39 |
| 5063803 | +40 |
| 6331519 | +91 |
| 6706067 | +45 |
| 7392257 | +40 |
| 8315831 | +3 |
| 8871167 | −85 |
| 9278443 | −75 |
| 9615329 | +27 |
| 9756727 | +23 |
| 10746881 | −7 |
| 11465149 | −62 |
| 11512541 | −26 |
| 11892977 | −7 |
| 12632117 | −27 |
| 12893203 | −53 |
| 14296621 | +2 |
| 16711069 | +95 |
| 16738091 | +58 |
| 17879887 | +63 |
| 19344553 | −93 |
| 19365641 | +75 |
| 20951477 | +25 |
| 20972977 | +58 |
| 21561013 | −90 |
| 23818681 | +23 |
| 27783521 | −51 |
| 27812887 | +21 |
| 29085907 | +9 |
| 29327513 | +13 |
| 30959321 | +24 |
| 33187157 | +60 |
| 33968041 | +12 |
| 39198017 | −7 |
| 45920923 | −63 |
| 51802061 | +4 |
| 53188379 | −54 |
| 56151923 | −1 |
| 57526411 | −66 |
| 64197799 | +13 |
| 72818227 | −27 |
| 87467099 | −2 |
| 91926437 | −32 |
| 92191909 | +94 |
| 93445061 | −30 |
| 93559087 | −3 |
| 94510219 | −69 |
| 101710369 | −70 |
| 111310567 | +22 |
| 117385529 | −43 |
| 176779259 | +56 |
| 212911781 | −92 |
| 216331463 | −36 |
| 253512533 | +25 |
| 282361201 | +24 |
| 327357841 | −62 |
| 411237857 | −84 |
| 479163953 | −50 |
| 757362197 | −28 |
| 824846833 | +60 |
| 866006431 | −81 |
| 1227886151 | −51 |
| 1527857939 | −19 |
| 1636804231 | +64 |
| 1686290297 | +18 |
| 1767839071 | +8 |
| 1913042311 | −65 |
| 1987272877 | +5 |
| 2100839597 | −34 |
| 2312420701 | −78 |
| 2476913683 | +94 |
| 3542985241 | −74 |
| 4036677373 | −5 |
| 4271431471 | +83 |
| 4296847931 | +41 |
| 5087988391 | +51 |
| 5127702389 | +50 |
| 7973760941 | +76 |
| 9965682053 | −18 |
| 10242692519 | −97 |
| 11355061259 | −45 |
| 11774118061 | −1 |
| 12896325149 | +86 |
| 13286279999 | +52 |
| 20042556601 | +27 |
| 21950810731 | +93 |
| 23607097193 | +97 |
| 24664241321 | +46 |
| 28737804211 | −58 |
| 35525054743 | +26 |
| 41659815553 | +55 |
| 42647052491 | +10 |
| 44034466379 | +39 |
| 60373446719 | −48 |
| 64643245189 | −21 |
| 66966581777 | +91 |
| 67133912011 | +9 |
| 80248324571 | +46 |
| 80908082573 | −20 |
| 100660783343 | +87 |
| 112825721339 | +70 |
| 231939720421 | +41 |
| 258818504023 | +4 |
| 260584487287 | −52 |
| 265784418461 | −78 |
| 298114694431 | +82 |
A prime p satisfying the congruence (p − 1)! ≡ − 1 + Bp mod p2 with small |B| can be called a near-Wilson prime. Near-Wilson primes with B = 0 represent Wilson primes. The following table lists all such primes with |B| ≤ 100 from 106 up to 4×1011:[2]
Wilson numbers
A Wilson number is a natural number n such that W(n) ≡ 0 (mod n2), where 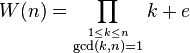 , the constant e = 1 if and only if n have a primitive root, otherwise, e = -1[9] For every natural number n, W(n) is divisible by n, and the quotients (called generalized Wilson quotients) are listed in
, the constant e = 1 if and only if n have a primitive root, otherwise, e = -1[9] For every natural number n, W(n) is divisible by n, and the quotients (called generalized Wilson quotients) are listed in ![]() A157249. The Wilson numbers are
A157249. The Wilson numbers are
- 1, 5, 13, 563, 5971, 558771, 1964215, 8121909, 12326713, 23025711, 26921605, 341569806, 399292158, ... (sequence A157250 in OEIS)
If a Wilson number n is prime, then n is a Wilson prime. There are 13 Wilson numbers up to 5×108.[10]
See also
Notes
- ↑ Lehmer, Emma (April 1938). "On congruences involving Bernoulli numbers and the quotients of Fermat and Wilson" (PDF). Annals of Mathematics 39 (2): 350–360. doi:10.2307/1968791. Retrieved 8 March 2011.
- 1 2 A Search for Wilson primes Retrieved on November 2, 2012.
- ↑ The Prime Glossary: Wilson prime
- ↑ McIntosh, R. (9 March 2004). "WILSON STATUS (Feb. 1999)". E-Mail to Paul Zimmermann. Retrieved 6 June 2011.
- ↑ A search for Wieferich and Wilson primes, p 443
- ↑ Ribenboim, P.; Keller, W. (2006). Die Welt der Primzahlen: Geheimnisse und Rekorde (in German). Berlin Heidelberg New York: Springer. p. 241. ISBN 3-540-34283-4.
- ↑ Ibercivis site
- ↑ Distributed search for Wilson primes (at mersenneforum.org)
- ↑ see Gauss's generalization of Wilson's theorem
- ↑ Agoh, Takashi; Dilcher, Karl; Skula, Ladislav (1998). "Wilson quotients for composite moduli" (PDF). Math. Comput. 67 (222): 843–861. doi:10.1090/S0025-5718-98-00951-X.
References
- Beeger, N. G. W. H. (1913–1914). "Quelques remarques sur les congruences rp−1 ≡ 1 (mod p2) et (p − 1!) ≡ −1 (mod p2)". The Messenger of Mathematics 43: 72–84.
- Goldberg, Karl (1953). "A table of Wilson quotients and the third Wilson prime". J. London Math. Soc. 28 (2): 252–256. doi:10.1112/jlms/s1-28.2.252.
- Ribenboim, Paulo (1996). The new book of prime number records. Springer-Verlag. p. 346. ISBN 0-387-94457-5.
- Crandall, Richard E.; Dilcher, Karl; Pomerance, Carl (1997). "A search for Wieferich and Wilson primes". Math. Comput. 66 (217): 433–449. doi:10.1090/S0025-5718-97-00791-6.
- Crandall, Richard E.; Pomerance, Carl (2001). Prime Numbers: A Computational Perspective. Springer-Verlag. p. 29. ISBN 0-387-94777-9.
- Pearson, Erna H. (1963). "On the Congruences (p − 1)! ≡ −1 and 2p−1 ≡ 1 (mod p2)" (PDF). Math. Comput. 17: 194–195.
External links
- The Prime Glossary: Wilson prime
- Weisstein, Eric W., "Wilson prime", MathWorld.
- Status of the search for Wilson primes
- "Wilson Quotients for composite moduli". CiteSeerX: 10
.1 ..1 .102 .6544 - On congruences involving Bernoulli numbers and the quotients of Fermat and Wilson
| ||||||||||||||||||||||||||||||||||||||||||||||