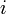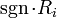Wilcoxon signed-rank test
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used when comparing two related samples, matched samples, or repeated measurements on a single sample to assess whether their population mean ranks differ (i.e. it is a paired difference test). It can be used as an alternative to the paired Student's t-test, t-test for matched pairs, or the t-test for dependent samples when the population cannot be assumed to be normally distributed.[1]
History
The test is named for Frank Wilcoxon (1892–1965) who, in a single paper, proposed both it and the rank-sum test for two independent samples (Wilcoxon, 1945).[2] The test was popularized by Sidney Siegel (1956) in his influential text book on non-parametric statistics.[3] Siegel used the symbol T for a value related to, but not the same as, 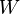 . In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.
. In consequence, the test is sometimes referred to as the Wilcoxon T test, and the test statistic is reported as a value of T.
Assumptions
- Data are paired and come from the same population.
- Each pair is chosen randomly and independently.
- The data are measured at least on an ordinal scale (cannot be nominal).
Test procedure
Let  be the sample size, the number of pairs. Thus, there are a total of 2N data points. For
be the sample size, the number of pairs. Thus, there are a total of 2N data points. For 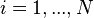 , let
, let 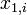 and
and 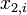 denote the measurements.
denote the measurements.
- H0: difference between the pairs follows a symmetric distribution around zero
- H1: difference between the pairs does not follow a symmetric distribution around zero.
- For
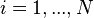 , calculate
, calculate  and
and 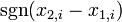 , where
, where 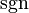 is the sign function.
is the sign function. - Exclude pairs with
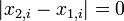 . Let
. Let  be the reduced sample size.
be the reduced sample size. - Order the remaining
 pairs from smallest absolute difference to largest absolute difference,
pairs from smallest absolute difference to largest absolute difference,  .
. - Rank the pairs, starting with the smallest as 1. Ties receive a rank equal to the average of the ranks they span. Let
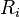 denote the rank.
denote the rank. - Calculate the test statistic
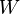
-
![W = \sum_{i=1}^{N_r} [\sgn(x_{2,i} - x_{1,i}) \cdot R_i]](../I/m/581d1a83ad20dc5eb35f6b0f49ec0647.png) , the sum of the signed ranks.
, the sum of the signed ranks.
-
- Under null hypothesis,
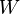 follows a specific distribution with no simple expression. This distribution has an expected value of 0 and a variance of
follows a specific distribution with no simple expression. This distribution has an expected value of 0 and a variance of 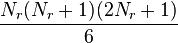 .
.
-
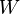 can be compared to a critical value from a reference table.[1]
can be compared to a critical value from a reference table.[1] - The two-sided test consists in rejecting
 , if
, if 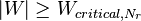 .
.
-
- As
 increases, the sampling distribution of
increases, the sampling distribution of  converges to a normal distribution. Thus,
converges to a normal distribution. Thus,
The T statistic used by Siegel is the smaller of two sums of ranks of given sign; in the example given below, therefore, T would equal 3+4+5+6=18. Low values of T are required for significance. As will be obvious from the example below, T is easier to calculate by hand than W and the test is equivalent to the two-sided test above-described (the distribution of the statistic under H0 has to be adjusted).
Excluding zeros is not a statistically justified method and such an approach can lead to enormous calculation errors. A more stable method is:[4]
- Calculate
![W = \sum_{i=1}^{N} [\sgn(x_{2,i} - x_{1,i}) \cdot R_i]](../I/m/1a6f29a396eab2cfefb454ade7b21d91.png) , (assume sgn(0) = 0)
, (assume sgn(0) = 0) - Calculate sampling probabilities
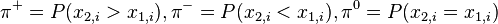
- For
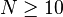 use normal approximation
use normal approximation 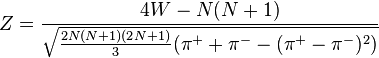 .
.
(Note that this value is undefined if either 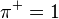 or
or 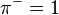 : i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)
: i.e. if all samples show positive effect or all samples show negative effect. This is not the case with the test statistic as originally defined.)
Example
|
order by absolute difference |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
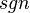 is the sign function,
is the sign function, 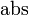 is the absolute value, and
is the absolute value, and 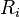 is the rank. Notice that pairs 3 and 9 are tied in absolute value. They would be ranked 1 and 2, so each gets the average of those ranks, 1.5.
is the rank. Notice that pairs 3 and 9 are tied in absolute value. They would be ranked 1 and 2, so each gets the average of those ranks, 1.5.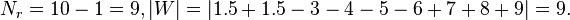
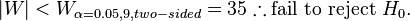
Effect size
To compute an effect size for the signed-rank test, one can use the rank correlation.
If the test statistic W is reported, Kerby (2014) has shown that the rank correlation r is equal to the test statistic W divided by the total rank sum S, or r = W/S.[5] Using the above example, the test statistic is W = 9. The sample size of 9 has a total rank sum of S = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 45. Hence, the rank correlation is 9/45, so r = 0.20.
If the test statistic T is reported, an equivalent way to compute the rank correlation is with the difference in proportion between the two rank sums, which is the Kerby (2014) simple difference formula.[5] To continue with the current example, the sample size is 9, so the total rank sum is 45. T is the smaller of the two rank sums, so T is 3 + 4 + 5 + 6 = 18. From this information alone, the remaining rank sum can be computed, because it is the total sum S minus T, or in this case 45 - 18 = 27. Next, the two rank-sum proportions are 27/45 = 60% and 18/45 = 40%. Finally, the rank correlation is the difference between the two proportions (.60 minus .40), hence r = .20.
Implementations
- ALGLIB includes implementation of the Wilcoxon signed-rank test in C++, C#, Delphi, Visual Basic, etc.
- The free statistical software R includes an implementation of the test as
wilcox.test(x,y, paired=TRUE), where x and y are vectors of equal length.[6] - GNU Octave implements various one-tailed and two-tailed versions of the test in the
wilcoxon_testfunction. - SciPy includes an implementation of the Wilcoxon signed-rank test in Python
See also
- Mann–Whitney–Wilcoxon test (the variant for two independent samples)
- Sign test (Like Wilcoxon test, but without the assumption of symmetric distribution of the differences around the median, and without using the magnitude of the difference)
References
- 1 2 Lowry, Richard. "Concepts & Applications of Inferential Statistics". Retrieved 24 March 2011.
- ↑ Wilcoxon, Frank (Dec 1945). "Individual comparisons by ranking methods" (PDF). Biometrics Bulletin 1 (6): 80–83.
- ↑ Siegel, Sidney (1956). Non-parametric statistics for the behavioral sciences. New York: McGraw-Hill. pp. 75–83.
- ↑ Ikewelugo Cyprian Anaene Oyeka (Apr 2012). "Modified Wilcoxon Signed-Rank Test". Open Journal of Statistics: 172–176.
- 1 2 Kerby, D. S. (2014). The simple difference formula: An approach to teaching nonparametric correlation. Innovative Teaching, volume 3, article 1. doi:10.2466/11.IT.3.1. link to pdf
- ↑ Dalgaard, Peter (2008). Introductory Statistics with R. Springer Science & Business Media. pp. 99–100. ISBN 978-0-387-79053-4.
External links
- Wilcoxon Signed-Rank Test in R
- Example of using the Wilcoxon signed-rank test
- An online version of the test
- A table of critical values for the Wilcoxon signed-rank test
- Brief guide by experimental psychologist Karl L. Weunsch - Nonparametric effect size estimators (Copyright 2015 by Karl L. Weunsch)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
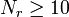 , a
, a 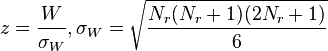 .
.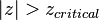 then reject
then reject