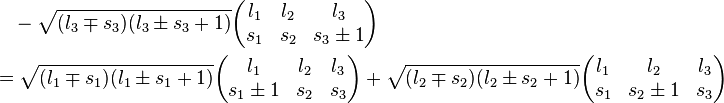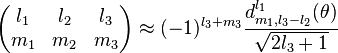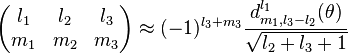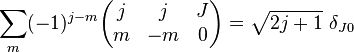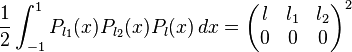3-j symbol
In quantum mechanics, the Wigner 3-j symbols, also called 3j or 3-jm symbols, are related to Clebsch–Gordan coefficients through
Inverse relation
The inverse relation can be found by noting that j1 − j2 − m3 is an integer and making the substitution m3 → −m3:
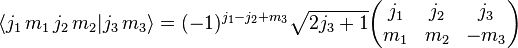 .
.
Note that the exponent of the sign factor is always an integer, therefore it remains the same under inversion.
Symmetry properties
The symmetry properties of 3j symbols are more convenient than those of Clebsch–Gordan coefficients. A 3j symbol is invariant under an even permutation of its columns:
An odd permutation of the columns gives a phase factor:
Changing the sign of the  quantum numbers also gives a phase:
quantum numbers also gives a phase:
Regge symmetries also give
Regge symmetries account for a total of 72 symmetries.[1] These are best displayed by the definition of a Regge symbol which is a one to one correspondence between it and a 3j symbol and assumes the properties of a semi-magic square[2]
whereby the 72 symmetries now correspond to 3! row and 3! column interchanges plus a transposition of the matrix. This can be used to devise an effective storage scheme.[3]
Selection rules
The Wigner 3-j symbol is zero unless all these conditions are satisfied:
Scalar invariant
The contraction of the product of three rotational states with a 3j symbol,
is invariant under rotations.
Orthogonality relations
Relation to spherical harmonics
The 3jm symbols give the integral of the products of three spherical harmonics
with  ,
, 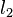 and
and 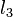 integers.
integers.
Relation to integrals of spin-weighted spherical harmonics
Similar relations exist for the spin-weighted spherical harmonics:
Recursion relations
Asymptotic expressions
For 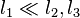 a non-zero 3-j symbol has
a non-zero 3-j symbol has
where 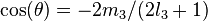 and
and 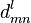 is a Wigner function. Generally a better approximation obeying the Regge symmetry is given by
is a Wigner function. Generally a better approximation obeying the Regge symmetry is given by
where 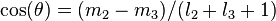 .
.
Other properties
See also
References
- ↑ Regge, T. (1958). "Symmetry Properties of Clebsch-Gordan Coefficients". Nuovo Cimento 10: 544. doi:10.1007/BF02859841.
- ↑ Rasch, J.; Yu, A. C. H. (2003). "Efficient Storage Scheme for Pre-calculated Wigner 3j, 6j and Gaunt Coefficients". SIAM J. Sci. Comput. 25 (4): 1416–1428. doi:10.1137/s1064827503422932.
- ↑ Rasch, J.; Yu, A. C. H. (2003). "Efficient Storage Scheme for Pre-calculated Wigner 3j, 6j and Gaunt Coefficients". SIAM J. Sci. Comput. 25 (4): 1416–1428. doi:10.1137/s1064827503422932.
- L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, volume 8 of Encyclopedia of Mathematics, Addison-Wesley, Reading, 1981.
- D. M. Brink and G. R. Satchler, Angular Momentum, 3rd edition, Clarendon, Oxford, 1993.
- A. R. Edmonds, Angular Momentum in Quantum Mechanics, 2nd edition, Princeton University Press, Princeton, 1960.
- Maximon, Leonard C. (2010), "3j,6j,9j Symbols", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- Varshalovich, D. A.; Moskalev, A. N.; Khersonskii, V. K. (1988). Quantum Theory of Angular Momentum. World Scientific Publishing Co.
- Regge, T. (1958). "Symmetry Properties of Clebsch-Gordon's Coefficients". Nuovo Cimento 10 (3): 544–545. doi:10.1007/BF02859841.
- E. P. Wigner, "On the Matrices Which Reduce the Kronecker Products of Representations of Simply Reducible Groups", unpublished (1940). Reprinted in: L. C. Biedenharn and H. van Dam, Quantum Theory of Angular Momentum, Academic Press, New York (1965).
- Moshinsky, Marcos (1962). "Wigner coefficients for the SU3 group and some applications". Rev. Mod. Phys. 34 (4): 813. Bibcode:1962RvMP...34..813M. doi:10.1103/RevModPhys.34.813.
- Baird, G. E.; Biedenharn, L. C. (1963). "On the representation of the semisimple Lie Groups. II.". J. Math. Phys. 4: 1449. Bibcode:1963JMP.....4.1449B. doi:10.1063/1.1703926.
- Swart de, J. J. (1963). "The octet model and its Glebsch-Gordan coefficients". Rev. Mod. Phys. 35 (4): 916. Bibcode:1963RvMP...35..916D. doi:10.1103/RevModPhys.35.916.
- Baird, G. E.; Biedenharn, L. C. (1964). "On the representations of the semisimple Lie Groups. III. The explicit conjugation Operation for SUn". J. Math. Phys. 5: 1723. Bibcode:1964JMP.....5.1723B. doi:10.1063/1.1704095.
- Horie, Hisashi (1964). "Representations of the symmetric group and the fractional parentage coefficients". J. Phys. Soc. Jpn. 19: 1783. Bibcode:1964JPSJ...19.1783H. doi:10.1143/JPSJ.19.1783.
- P. McNamee, S. J.; Chilton, Frank (1964). "Tables of Clebsch-Gordan coefficients of SU3". Rev. Mod. Phys. 36 (4): 1005. Bibcode:1964RvMP...36.1005M. doi:10.1103/RevModPhys.36.1005.
- Hecht, K. T. (1965). "SU3 recoupling and fractional parentage in the 2s-1d shell". Nucl. Phys. 62 (1): 1. Bibcode:1965NucPh..62....1H. doi:10.1016/0029-5582(65)90068-4.
- Itzykson, C.; Nauenberg, M. (1966). "Unitary groups: representations and decompositions". Rev. Mod. Phys. 38 (1): 95. Bibcode:1966RvMp...38...95I. doi:10.1103/RevModPhys.38.95.
- Kramer, P. (1967). "Orbital fractional parentage coefficients for the harmonic oscillator shell model". Z. Phys. 205 (2): 181. Bibcode:1967ZPhy..205..181K. doi:10.1007/BF01333370.
- Kramer, P. (1968). "Recoupling coefficients of the symmetric group for shell and cluster model configurations". Z. Phys. 216 (1): 68. Bibcode:1968ZPhy..216...68K. doi:10.1007/BF01380094.
- Hecht, K. T.; Pang, Sing Ching (1969). "On the Wigner Supermultiplet Scheme". J. Math. Phys. 10 (9): 1571. Bibcode:1969JMP....10.1571H. doi:10.1063/1.1665007.
- Lezuo, K. J. (1972). "The symmetric group and the Gel'fand basis of U(3). Generalizations of the Dirac identity". J. Math. Phys. 13 (9): 1389. Bibcode:1972JMP....13.1389L. doi:10.1063/1.1666151.
- Draayer, J. P.; Akiyama, Yoshimi (1973). "Wigner and Racah coefficients for SU3". J. Math. Phys. 14 (12): 1904. Bibcode:1973JMP....14.1904D. doi:10.1063/1.1666267.
- Akiyama, Yoshimi; Draayer, J. P. (1973). "A users' guide to fortran programs for Wigner and Racah coefficients of SU3". Comp. Phys. Comm. 5: 405. Bibcode:1973CoPhC...5..405A. doi:10.1016/0010-4655(73)90077-5.
- Paldus, Josef (1974). "Group theoretical approach to the configuration interaction and perturbation theory calculations for atomic and molecular systems". J. Chem. Phys 61 (12): 5321. Bibcode:1974JChPh..61.5321P. doi:10.1063/1.1681883.
- Schulten, Klaus; Gordon, Roy G. (1975). "Exact recursive evaluation of 3j and 6j-coefficients for quantum mechanical coupling of angular momenta". J. Math. Phys. 16 (10): 1961–1970. Bibcode:1975JMP....16.1961S. doi:10.1063/1.522426.
- Haacke, E. M.; Moffat, J. W.; Savaria, P. (1976). "A calculation of SU(4) Glebsch-Gordan coefficients". J. Math. Phys. 17 (11): 2041. Bibcode:1976JMP....17.2041H. doi:10.1063/1.522843.
- Paldus, Josef (1976). "Unitary-group approach to the many-electron correlation problem: Relation of Gelfand and Weyl tableau formulations". Phys. Rev. A 14 (5): 1620. Bibcode:1976PhRvA..14.1620P. doi:10.1103/PhysRevA.14.1620.
- Bickerstaff, R. P.; Butler, P. H.; Butts, M. B.; Haase, R. w.; Reid, M. F. (1982). "3jm and 6j tables for some bases of SU6 and SU3". J. Phys. A 15: 1087. Bibcode:1982JPhA...15.1087B. doi:10.1088/0305-4470/15/4/014.
- Sarma, C. R.; Sahasrabudhe, G. G. (1980). "Permutational symmetry of many particle states". J. Math. Phys. 21 (4): 638. Bibcode:1980JMP....21..638S. doi:10.1063/1.524509.
- Chen, Jin-Quan; Gao, Mei-Juan (1982). "A new approach to permutation group representation". J. Math. Phys. 23: 928. Bibcode:1982JMP....23..928C. doi:10.1063/1.525460.
- Sarma, C. R. (1982). "Determination of basis for the irreducible representations of the unitary group for U(p+q)↓U(p)×U(q)". J. Math. Phys. 23 (7): 1235. Bibcode:1982JMP....23.1235S. doi:10.1063/1.525507.
- Chen, J.-Q.; Chen, X.-G. (1983). "The Gel'fand basis and matrix elements of the graded unitary group U(m/n)". J. Phys. A 16 (15): 3435. Bibcode:1983JPhA...16.3435C. doi:10.1088/0305-4470/16/15/010.
- Nikam, R. S.; Dinesha, K. V.; Sarma, C. R. (1983). "Reduction of inner-product representations of unitary groups". J. Math. Phys. 24 (2): 233. Bibcode:1983JMP....24..233N. doi:10.1063/1.525698.
- Chen, Jin-Quan; Collinson, David F.; Gao, Mei-Juan (1983). "Transformation coefficients of permutation groups". J. Math. Phys. 24: 2695. Bibcode:1983JMP....24.2695C. doi:10.1063/1.525668.
- Chen, Jin-Quan; Gao, Mei-Juan; Chen, Xuan-Gen (1984). "The Clebsch-Gordan coefficient for SU(m/n) Gel'fand basis". J. Phys. A 17 (3): 481. Bibcode:1984JPhA...17..727K. doi:10.1088/0305-4470/17/3/011.
- Srinivasa Rao, K. (1985). "Special topics in the quantum theory of angular momentum". Pramana 24 (1): 15–26. Bibcode:1985Prama..24...15R. doi:10.1007/BF02894812.
- Wei, Liqiang (1999). "Unified approach for exact calculation of angular momentum coupling and recoupling coefficients". Comp. Phys. Comm. 120 (2–3): 222–230. Bibcode:1999CoPhC.120..222W. doi:10.1016/S0010-4655(99)00232-5.
- Rasch, J.; Yu, A. C. H. (2003). "Efficient Storage Scheme for Pre-calculated Wigner 3j, 6j and Gaunt Coefficients". SIAM J. Sci. Comput. 25 (4): 1416–1428. doi:10.1137/s1064827503422932.
External links
- Stone, Anthony. "Wigner coefficient calculator".
- Volya, A. "Clebsch-Gordan, 3-j and 6-j Coefficient Web Calculator". (Numerical)
- Stevenson, Paul. "Clebsch-O-Matic". Bibcode:2002CoPhC.147..853S. doi:10.1016/S0010-4655(02)00462-9.
- 369j-symbol calculator at the Plasma Laboratory of Weizmann Institute of Science (Numerical)
- Frederik J Simons: Matlab software archive, the code THREEJ.M
- Sage (mathematics software) Gives exact answer for any value of j, m
- Johansson, H.T.; Forssén, C. "(WIGXJPF)". (accurate; C, fortran, python)
- Johansson, H.T. "(FASTWIGXJ)". (fast lookup, accurate; C, fortran)
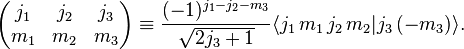
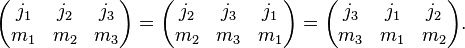
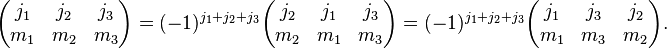
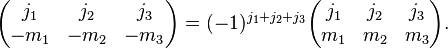
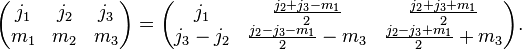
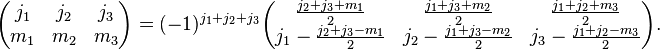
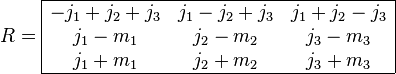

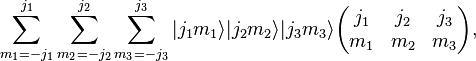
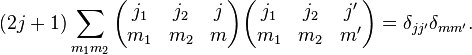
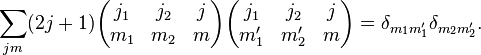
![\begin{align}
& {} \quad \int Y_{l_1m_1}(\theta,\varphi)Y_{l_2m_2}(\theta,\varphi)Y_{l_3m_3}(\theta,\varphi)\,\sin\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi \\
& =
\sqrt{\frac{(2l_1+1)(2l_2+1)(2l_3+1)}{4\pi}}
\begin{pmatrix}
l_1 & l_2 & l_3 \\[8pt]
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
l_1 & l_2 & l_3\\
m_1 & m_2 & m_3
\end{pmatrix}
\end{align}](../I/m/3d701a69eb30c470385a582e40b73b5c.png)
![\begin{align}
& {} \quad \int d{\mathbf{\hat n}}\,{}_{s_1} Y_{j_1 m_1}({\mathbf{\hat n}})
\,{}_{s_2} Y_{j_2m_2}({\mathbf{\hat n}})\, {}_{s_3} Y_{j_3m_3}({\mathbf{\hat
n}}) \\[8pt]
& = \sqrt{\frac{(2j_1+1)(2j_2+1)(2j_3+1)}{4\pi}}
\begin{pmatrix}
j_1 & j_2 & j_3\\
m_1 & m_2 & m_3
\end{pmatrix}
\begin{pmatrix}
j_1 & j_2 & j_3\\
-s_1 & -s_2 & -s_3
\end{pmatrix}
\end{align}](../I/m/42fce865d657e4b785980bf06d197590.png)