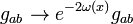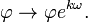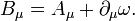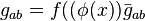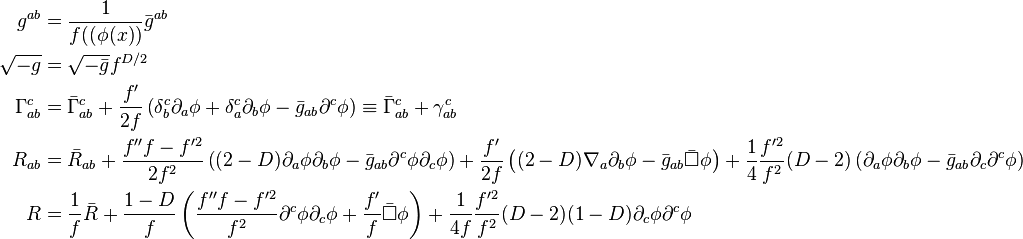Weyl transformation
- See also Wigner–Weyl transform, for another definition of the Weyl transform.
In theoretical physics, the Weyl transformation, named after Hermann Weyl, is a local rescaling of the metric tensor:
which produces another metric in the same conformal class. A theory or an expression invariant under this transformation is called conformally invariant, or is said to possess Weyl symmetry. The Weyl symmetry is an important symmetry in conformal field theory. It is, for example, a symmetry of the Polyakov action.
The ordinary Levi-Civita connection and associated spin connections are not invariant under Weyl transformations. An appropriately invariant notion is the Weyl connection, which is one way of specifying the structure of a conformal connection.
A quantity φ has conformal weight k if, under the Weyl transformation, it transforms via
Thus conformally weighted quantities belong to certain density bundles; see also conformal dimension. Let Aμ be the connection one-form associated to the Levi-Civita connection of g. Introduce a connection that depends also on an initial one-form 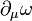 via
via
Then 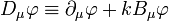 is covariant and has conformal weight
is covariant and has conformal weight  .
.
Formulas
For the transformation
We can derive the following formulas
Note that the Weyl tensor is invariant under a Weyl rescaling.
Literature
- Hermann Weyl, Raum, Zeit, Materie (Space, Time, Matter), Lectures on General Relativity, in German. Berlin, Springer 1921, with later reprints in 1993. ISBN 3-540-56978-2