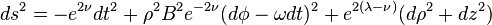Weyl−Lewis−Papapetrou coordinates

General relativity
Introduction History Mathematical formulation Resources Tests
Fundamental concepts Equivalence principle Special relativity World line Riemannian geometry
Phenomena Kepler problem Gravitational lensing Gravitational waves Frame-dragging Geodetic effect Event horizon Singularity Black hole Spacetime Spacetime diagrams Minkowski spacetime Einstein–Rosen bridge
Equations Formalisms Equations Linearized gravity Einstein field equations Friedmann Geodesics Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalisms ADM BSSN Post-Newtonian Advanced theory Kaluza–Klein theory Quantum gravity
Solutions Schwarzschild Reissner–Nordström Gödel Kerr Kerr–Newman Kasner Lemaître–Tolman Taub-NUT Milne Robertson–Walker pp-wave van Stockum dust
Scientists Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedman Milne Zwicky Lemaître Gödel Wheeler Robertson Bardeen Walker Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Newman Yau Thorne others

In general relativity, the Weyl−Lewis−Papapetrou coordinates are a set of coordinates, used in the solutions to the vacuum region surrounding an axisymmetric distribution of mass–energy. They are named for Hermann Weyl, T. Lewis, and Achilles Papapetrou.

The square of the line element is of the form:^[1]

where (t, ρ, ϕ, z) are the cylindrical Weyl−Lewis−Papapetrou coordinates in 3 + 1 spacetime, and λ, ν, ω, and B, are unknown functions of the spatial non-angular coordinates ρ and z only. Different authors define the functions of the coordinates differently.

See also

• Introduction to the mathematics of general relativity
• Stress–energy tensor
• Metric tensor (general relativity)
• Relativistic angular momentum

References

Selected papers

• J. Marek; A. Sloane (1979). "A finite rotating body in general relativity". Il Nuovo Cimento B Series 11 51 (1). pp. 45–52. 

• L. Richterek; J. Novotny; J. Horsky (2002). "Einstein−Maxwell fields generated from the gamma-metric and their limits" (PDF). Czech.J.Phys. 52. p. 2. arXiv:gr-qc/0209094v1. doi:10.1023/A:1020581415399. 

• M. Sharif (2007). "Energy-Momentum Distribution of the Weyl−Lewis−Papapetrou and the Levi-Civita Metrics" (PDF). Brazilian Journal of Physics 37. 

• A. Sloane (1978). "The axially symmetric stationary vacuum field equations in Einstein's theory of general relativity". Aust. J. Phys 31 (CSIRO). p. 429. Bibcode:1978AuJPh..31..427S. 

Selected books

• J. L. Friedman; N. Stergioulas (2013). Rotating Relativistic Stars. Cambridge Monographs on Mathematical Physics. Cambridge University Press. p. 151. ISBN 052-187-254-5. 

• A. Macías; J. L. Cervantes-Cota; C. Lämmerzahl (2001). Exact Solutions and Scalar Fields in Gravity: Recent Developments. Springer. p. 39. ISBN 030-646-618-X. 

• A. Das; A. DeBenedictis (2012). The General Theory of Relativity: A Mathematical Exposition. Springer. p. 317. ISBN 146-143-658-3. 

• G. S. Hall; J. R. Pulham (1996). General relativity: proceedings of the forty sixth Scottish Universities summer school in physics, Aberdeen, July 1995. SUSSP proceedings 46. Scottish Universities Summer School in Physics. pp. 65, 73, 78. ISBN 075-030-395-6.