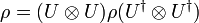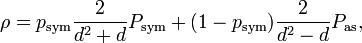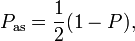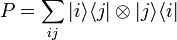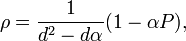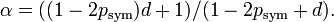Werner state

A Werner state^[1] is a d × d-dimensional bipartite quantum state density matrix that is invariant under all unitary operators of the form 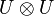$U \otimes U$ . That is, it is a quantum state ρ that satisfies

\rho = (U \otimes U) \rho (U^\dagger \otimes U^\dagger)

for all unitary operators U acting on d-dimensional Hilbert space.

Every Werner state is a mixture of projectors onto the symmetric and antisymmetric subspaces, with the relative weight p_sym being the only parameter that defines the state.

\rho = p_\text{sym} \frac{2}{d^2 + d} P_\text{sym} + (1-p_\text{sym}) \frac{2}{d^2 - d} P_\text{as},

where

P_\text{sym} = \frac{1}{2}(1+P),

P_\text{as} = \frac{1}{2}(1-P),

are the projectors and

P = \sum_{ij} |i\rangle \langle j| \otimes |j\rangle \langle i|

is the permutation operator that exchanges the two subsystems.

Werner states are separable for p_sym ≥ ¹⁄₂ and entangled for p_sym < ¹⁄₂. All entangled Werner states violate the PPT separability criterion, but for d ≥ 3 no Werner states violate the weaker reduction criterion. Werner states can be parametrized in different ways. One way of writing them is

\rho = \frac{1}{d^2-d \alpha}(1 - \alpha P),

where the new parameter α varies between −1 and 1 and relates to p_sym as

\alpha = ((1-2p_\text{sym})d+1)/(1-2p_\text{sym}+d) .

Multipartite Werner states

Werner states can be generalized to the multipartite case.^[2] An N-party Werner state is a state that is invariant under 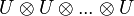$U \otimes U \otimes ... \otimes U$ for any unitary U on a single subsystem. The Werner state is no longer described by a single parameter, but by N! − 1 parameters, and is a linear combination of the N! different permutations on N systems.

References

↑ Reinhard F. Werner (1989). "Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model". Physical Review A 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. PMID 9902666.
↑ Eggeling et al. (2008)

This article is issued from Wikipedia - version of the Thursday, August 29, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.