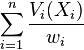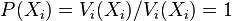Weller's theorem

Weller's theorem^[1] is a theorem in economics. It says that a cake can be divided among n partners with different preferences in a way that is both Pareto-efficient (PE) and envy-free (EF). Thus, it is possible to divide a cake fairly without compromising on economic efficiency.

Moreover, Weller's theorem says that there exists a price such that the allocation and the price are a competitive equilibrium with equal incomes. Thus, it connects two research fields which were previously unrelated: fair cake-cutting and general equilibrium.

Background

Fair cake-cutting has been studied since the 1940s. There is a heterogeneous divisible resource, such as a cake or a land-estate. There are n partners, each of whom has a personal value-density function over the cake. The value of a piece to a partner is the integral of his value-density over that piece (this means that the value is a nonatomic measure over the cake). The envy-free cake-cutting problem is to partition the cake to n disjoint pieces, one piece per agent, such for each agent, the value of his piece is weakly larger than the values of all other pieces (so no agent envies another agent's share).

A corollary of the Dubins–Spanier convexity theorem (1961) is that there always exists a "consensus partition" - a partition of the cake to n pieces such that every agent values every piece as exactly 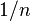$1/n$ . A consensus partition is of course EF, but it is not PE. Moreover, another corollary of the Dubins–Spanier convexity theorem is that, when at least two agents have different value measures, there exists a division that gives each agent strictly more than 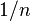$1/n$ . This means that the consensus partition is not even weakly PE.

Envy-freeness, as a criterion for fair allocation, were introduced into economics in the 1960s and studied intensively during the 1970s. Varian's theorems study it in the context of dividing homogeneous goods. Under certain restrictions on the agents' utility functions, there exist allocations which are both PE and EF. The proof uses a previous result on the existence of a competitive equilibrium. David Gale proved a similar existence result for agents with linear utilities.

Cake-cutting is more challenging than homogeneous good allocation, since a cake is heteroeneous. In a sense, a cake is a continuum of goods: each point in the cake is a different good. This is the topic of Weller's theorem.

Proof sketch

Weller's proof relies on weighted-utilitarian-maximal (WUM) cake divisions. A WUM division is a division maximizing a function of the following form:

\sum_{i=1}^{n}{V_i(X_i) \over w_i}

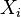where $i$ is an index of an agent, $V_i$ is agent $i$ 's value measure, $X_i$ is the piece given to $i$ , and $w_i$ is a positive weight.

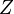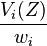A corollary of the Dubins–Spanier compactness theorem is that WUM allocations always exist. Intuitively, each tiny piece of cake $Z$ should be given to the person $i$ for whom ${V_i(Z) \over w_i}$ is largest. If there are two or more people for whom this value is the same, then every arbitrary division of that piece between them results in a WUM division.

Every WUM division is obviously PE. However, a WUM division can be very unfair; for example, if $w_i$ is very small, then agent $i$ might get the entire cake; if $w_i$ is very large, then agent $i$ might get no cake at all.

Weller's idea is to prove that there exists a vector of weights for which the WUM division is also EF. This is done as follows:

For every weight vector $w=[w_1,\dots,w_n]$ , find all WUM divisions.
For every such division, consider the vector of values enjoyed by the people, i.e. the vector: $[V_1(X_1),\dots,V_n(X_n)]$ . Make this the new set of weight vectors and return to step 1.
By the Kakutani fixed-point theorem, this process has a fixed point, i.e., there is a vector $w$ such that one of the WUM divisions belonging to $w$ generates a vector of values proportional to $w$ . It is possible to show that such division is EF.

Calculating the price measure

Once we have a PEEF allocation $X$ , a price measure $P$ can be calculated as follows:

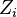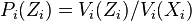
For every piece $Z_i$ that is held entirely by agent $i$ , $P_i(Z_i) = V_i(Z_i)/V_i(X_i)$
For every piece divided among several agent, the price is the sum of prices of its subsets held by these agents.

It is possible to prove that the pair 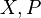$X,P$ satisfy the conditions of competitive equilibrium with equal incomes. Specifically, the income of every agent, under the price measure $P$ , is exactly 1, since:

P(X_i) = V_i(X_i)/V_i(X_i) = 1

Example

As an illustration, consider a cake with two parts: chocolate and vanilla, and two partners: Alice and George, with the following valuations:

Partner	Chocolate	Vanilla
Alice	9	1
George	6	4

Since there are two agents, the vector $w$ can be represented by a single number - the ratio of the weight of Alice to the weight of George:

If the ratio is less than 1:4, then a WUM division should give the entire cake to Alice. The ratio of values enjoyed by the people will be infinite (or 1:0), so of course no fixed point will be found in this range.
If the ratio is exactly 1:4, then the entire chocolate should be given to Alice, but the vanilla can be divided arbitrarily between Alice and George. The ratio of values of the WUM divisions ranges between 1:0 and 9:4. This range does not contain the ratio 1:4, hence the fixed point is not here.
If the ratio is between 1:4 and 9:6, then the entire vanilla should be given to George and the entire chocolate should be given to Alice. The ratio of values is 9:4, which is not in the range, so the fixed point is not found yet.
If the ratio is exactly 9:6, then the entire vanilla should be given to George but the chocolate can be divided arbitrarily between Alice and George. The ratio of values of the WUM divisions ranges between 9:4 and 0:1. We see that 9:6 is in the range so we have a fixed point. It can be achieved by giving to George the entire vanilla and 1/6 of the chocolate (for a total value of 5) and giving to Alice the remaining 5/6 of the chocolate (for a total value of 7.5). This division is PEEF.

Generalizations and extensions

Weller's theorem has a nice geometric interpretation based on the Radon–Nikodym set.

Berliant, Thomson and Dunz^[2] introduced the criterion of group envy-freeness, which generalizes both Pareto-efficiency and envy-freeness. They proved the existence of group-envy-free allocations with additive utilities. Later, Berliant and Dunz^[3] studied some natural non-additive utility functions, motivated by the problem of land division. When utilities are not additive, a PEEF allocation is no longer guaranteed to exist, but it does exist under certain restrictions.

More related results can be found in Efficient cake-cutting and Utilitarian cake-cutting.

Algorithms

Weller's theorem is purely existential. Some later authors studied the algorithmic aspects of finding a PEEF division:

If the value measures are piecewise-constant, then there is an algorithm that finds a PEEF division.^[4]

If the value measures are Lipschitz continuous, then they can be approximated as piecewise-constant functions "as close as we like", therefore that algorithm approximates a PEEF division "as close as we like".^[4]

References

↑ Weller, Dietrich (1985). "Fair division of a measurable space". Journal of Mathematical Economics 14: 5. doi:10.1016/0304-4068(85)90023-0.
↑ Berliant, M.; Thomson, W.; Dunz, K. (1992). "On the fair division of a heterogeneous commodity". Journal of Mathematical Economics 21 (3): 201. doi:10.1016/0304-4068(92)90001-n.
↑ Berliant, Marcus; Dunz, Karl (2004). "A foundation of location theory: Existence of equilibrium, the welfare theorems, and core". Journal of Mathematical Economics 40 (5): 593. doi:10.1016/s0304-4068(03)00077-6.
1 2 Reijnierse, J. H.; Potters, J. A. M. (1998). "On finding an envy-free Pareto-optimal division". Mathematical Programming 83: 291. doi:10.1007/bf02680564.

This article is issued from Wikipedia - version of the Monday, December 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.