Weighted space

In functional analysis, a weighted space is a space of functions under a weighted norm, which is a finite norm (or semi-norm) that involves multiplication by a particular function referred to as the weight.

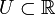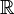Weights can be used to expand or reduce a space of considered functions. For example, in the space of functions from a set $U\subset\mathbb{R}$ to $\mathbb{R}$ under the norm $\|\cdot\|_U$ defined by: 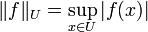$\|f\|_U=\sup_{x\in U}{|f(x)|}$ , functions that have infinity as a limit point are excluded. However, the weighted norm 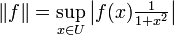$\|f\|=\sup_{x\in U}{\left|f(x)\tfrac{1}{1+x^2}\right|}$ is finite for many more functions, so the associated space contains more functions. Alternatively, the weighted norm $\|f\|=\sup_{x\in U}{\left|f(x)x^4\right|}$ is finite for many fewer functions.

When the weight is of the form $\tfrac{1}{1+x^m}$ , the weighted space is called polynomial-weighted.^[1]

References

↑ Walczak, Zbigniew (2005). "On the rate of convergence for some linear operators" (PDF). Hiroshima Mathematical Journal 35: 115–124.

Kudryavtsev, L D (2001). "Weighted Space". In Michiel Hazewinkel. Encyclopaedia of Mathematics. Springer.

This article is issued from Wikipedia - version of the Tuesday, September 10, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.