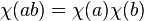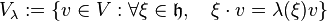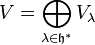Weight (representation theory)

In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.

Motivation and general concept

Weights

Given a set S of matrices, each of which is diagonalizable, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of S.^{[note 1]}^{[note 2]} Equivalently, for any set S of mutually commuting semisimple linear transformations of a finite-dimensional vector space V there exists a basis of V consisting of simultaneous eigenvectors of all elements of S. Each of these common eigenvectors v ∈ V defines a linear functional on the subalgebra U of End(V) generated by the set of endomorphisms S; this functional is defined as the map which associates to each element of U its eigenvalue on the eigenvector v. This map is also multiplicative, and sends the identity to 1; thus it is an algebra homomorphism from U to the base field. This "generalized eigenvalue" is a prototype for the notion of a weight.

The notion is closely related to the idea of a multiplicative character in group theory, which is a homomorphism χ from a group G to the multiplicative group of a field F. Thus χ: G → F^× satisfies χ(e) = 1 (where e is the identity element of G) and

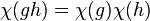\chi(gh) = \chi(g)\chi(h)

for all g, h in G.

Indeed, if G acts on a vector space V over F, each simultaneous eigenspace for every element of G, if such exists, determines a multiplicative character on G: the eigenvalue on this common eigenspace of each element of the group.

The notion of multiplicative character can be extended to any algebra A over F, by replacing χ: G → F^× by a linear map χ: A → F with:

\chi(ab) = \chi(a)\chi(b)

for all a, b in A. If an algebra A acts on a vector space V over F to any simultaneous eigenspace, this corresponds an algebra homomorphism from A to F assigning to each element of A its eigenvalue.

If A is a Lie algebra, then the commutativity of the field and the anticommutativity of the Lie bracket imply that this map vanish on commutators : χ([a,b])=0. A weight on a Lie algebra g over a field F is a linear map λ: g → F with λ([x, y])=0 for all x, y in g. Any weight on a Lie algebra g vanishes on the derived algebra [g,g] and hence descends to a weight on the abelian Lie algebra g/[g,g]. Thus weights are primarily of interest for abelian Lie algebras, where they reduce to the simple notion of a generalized eigenvalue for space of commuting linear transformations.

If G is a Lie group or an algebraic group, then a multiplicative character θ: G → F^× induces a weight χ = dθ: g → F on its Lie algebra by differentiation. (For Lie groups, this is differentiation at the identity element of G, and the algebraic group case is an abstraction using the notion of a derivation.)

Weight space of a representation of a Lie algebra

Among the set of weights, some are related to the data of a representation. Let V be a representation of a Lie algebra g over a field F and let λ be a weight of g. Then the weight space of V with weight λ: ħ → F (ħ is the Cartan subalgebra of g.) is the subspace

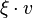V_\lambda:=\{v\in V: \forall \xi\in \mathfrak{h},\quad \xi\cdot v=\lambda(\xi)v\}

(where $\xi \cdot v$ denotes the action of ħ on V). A weight of the representation V is a weight λ such that the corresponding weight space is nonzero. Nonzero elements of the weight space are called weight vectors.

If V is the direct sum of its weight spaces

V=\bigoplus_{\lambda\in\mathfrak{h}^*} V_\lambda

then it is called a weight module; this corresponds to there being a common eigenbasis (a basis of simultaneous eigenvectors) for all the represented elements of the algebra, i.e., to their being simultaneously diagonalizable matrices (see diagonalizable matrix).

Similarly, we can define a weight space V_λ for any representation of a Lie group or an associative algebra.

Semisimple Lie algebras

Let g be a Lie algebra, h a maximal commutative Lie subalgebra consisting of semi-simple elements (sometimes called Cartan subalgebra) and let V be a finite dimensional representation of g. If g is semisimple, then [g, g] = g and so all weights on g are trivial. However, V is, by restriction, a representation of h, and it is well known that V is a weight module for h, i.e., equal to the direct sum of its weight spaces. By an abuse of language, the weights of V as a representation of h are often called weights of V as a representation of g.

Similar definitions apply to a Lie group G, a maximal commutative Lie subgroup H and any representation V of G. Clearly, if λ is a weight of the representation V of G, it is also a weight of V as a representation of the Lie algebra g of G.

If V is the adjoint representation of g, its weights are called roots, the weight spaces are called root spaces, and weight vectors are sometimes called root vectors.

We now assume that g is semisimple, with a chosen Cartan subalgebra h and corresponding root system. Let us suppose also that a choice of positive roots Φ⁺ has been fixed. This is equivalent to the choice of a set of simple roots.

Ordering on the space of weights

Let h*₀ be the real subspace of h* (if it is complex) generated by the roots of g.

There are two concepts how to define an ordering of h*₀.

The first one is

μ ≤ λ if and only if λ − μ is nonnegative linear combination of simple roots.

The second concept is given by an element f in h₀ and

μ ≤ λ if and only if μ(f) ≤ λ(f).

Usually, f is chosen so that β(f) > 0 for each positive root β.

Integral weight

A weight λ ∈ h* is integral (or g-integral), if λ(H_γ) ∈ Z for each coroot H_γ such that γ is a positive root.

The fundamental weights 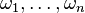$\omega_1,\ldots,\omega_n$ are defined by the property that they form a basis of h* dual to the set of simple coroots $H_{\alpha_1}, \ldots, H_{\alpha_n}$ .

Hence λ is integral if it is an integral combination of the fundamental weights. The set of all g-integral weights is a lattice in h* called weight lattice for g, denoted by P(g).

A weight λ of the Lie group G is called integral, if for each t in h such that 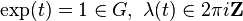$\exp(t)=1\in G,\,\,\lambda(t)\in 2\pi i \mathbf{Z}$ . For G semisimple, the set of all G-integral weights is a sublattice P(G) ⊂ P(g). If G is simply connected, then P(G) = P(g). If G is not simply connected, then the lattice P(G) is smaller than P(g) and their quotient is isomorphic to the fundamental group of G.^[1]

Dominant weight

A weight λ is dominant if 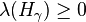$\lambda(H_\gamma)\geq 0$ for each coroot H_γ such that γ is a positive root. Equivalently, λ is dominant, if it is a non-negative linear combination of the fundamental weights.

The convex hull of the dominant weights is sometimes called the fundamental Weyl chamber.

Sometimes, the term dominant weight is used to denote a dominant (in the above sense) and integral weight.

Highest weight

A weight λ of a representation V is called a highest weight if no other weight of V is larger than λ in the partial order given above. Sometimes, one imposes the stronger condition that all other weights of V are strictly smaller than λ in the partial order. The term highest weight often suggests (or denotes) the highest weight of a "highest-weight module".

One defines a lowest weight similarly.

The space of all possible weights is a vector space. Let's fix a total ordering of this vector space such that a nonnegative linear combination of positive vectors with at least one nonzero coefficient is another positive vector.

Then, a representation is said to have highest weight λ if λ is a weight and all its other weights are less than λ.

Similarly, it is said to have lowest weight λ if λ is a weight and all its other weights are greater than it.

A weight vector 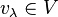$v_\lambda \in V$ of weight λ is called a highest-weight vector, or vector of highest weight, if all other weights of V are smaller than λ.

Highest-weight module

A representation V of g is called highest-weight module if it is generated by a weight vector v ∈ V that is annihilated by the action of all positive root spaces in g. Every finite-dimensional, irreducible representation of a semisimple Lie algebra g is a highest-weight module, and the representations can be classified by their highest weights ("theorem of the highest weight").^[2]

This is something more special than a g-module with a highest weight.

Similarly we can define a highest-weight module for representation of a Lie group or an associative algebra.

Verma module

Main article: Verma module

For each dominant weight λ ∈ h*, there exists a unique (up to isomorphism) simple highest-weight g-module with highest weight λ, which is denoted L(λ).

It can be shown that each highest weight module with highest weight λ is a quotient of the Verma module M(λ). This is just a restatement of universality property in the definition of a Verma module.

A highest-weight module is a weight module. The weight spaces in a highest-weight module are always finite dimensional.

Notes

↑ The converse is also true – a set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable (Horn & Johnson 1985, pp. 51–53).
↑ In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that they are diagonalizable.

References

↑ Hall 2015 Corollary 13.8 and Corollary 13.20
↑ Hall 2015 Theorems 9.4 and 9.5

Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6 .
Goodman, Roe; Wallach, Nolan R. (1998), Representations and Invariants of the Classical Groups, Cambridge University Press, ISBN 978-0-521-66348-9 .
Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics 222 (2nd ed.), Springer
Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
Humphreys, James E. (1972a), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7 .
Humphreys, James E. (1972b), Linear Algebraic Groups, Graduate Texts in Mathematics 21, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90108-4, MR 0396773

Knapp, Anthony W. (2002), Lie Groups Beyond an Introduction (2nd ed.), Birkhäuser, ISBN 978-0-8176-4259-4 .

This article is issued from Wikipedia - version of the Monday, December 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.