Woodin cardinal
In set theory, a Woodin cardinal (named for W. Hugh Woodin) is a cardinal number λ such that for all functions
- f : λ → λ
there exists a cardinal κ < λ with
- {f(β)|β < κ} ⊆ κ
and an elementary embedding
- j : V → M
from the Von Neumann universe V into a transitive inner model M with critical point κ and
- Vj(f)(κ) ⊆ M.
An equivalent definition is this: λ is Woodin if and only if λ is strongly inaccessible and for all 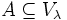 there exists a
there exists a 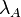 < λ which is
< λ which is 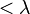 -
- -strong.
-strong.
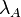 being
being 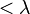 -
- -strong means that for all ordinals α < λ, there exist a
-strong means that for all ordinals α < λ, there exist a 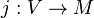 which is an elementary embedding with critical point
which is an elementary embedding with critical point 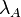 ,
, 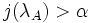 ,
, 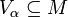 and
and 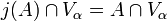 . (See also strong cardinal.)
. (See also strong cardinal.)
A Woodin cardinal is preceded by a stationary set of measurable cardinals, and thus it is a Mahlo cardinal. However, the first Woodin cardinal is not even weakly compact.
Consequences
Woodin cardinals are important in descriptive set theory. By a result[1] of Martin and Steel, existence of infinitely many Woodin cardinals implies projective determinacy, which in turn implies that every projective set is measurable, has the Baire property (differs from an open set by a meager set, that is, a set which is a countable union of nowhere dense sets), and the perfect set property (is either countable or contains a perfect subset).
The consistency of the existence of Woodin cardinals can be proved using determinacy hypotheses. Working in ZF+AD+DC one can prove that 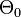 is Woodin in the class of hereditarily ordinal-definable sets.
is Woodin in the class of hereditarily ordinal-definable sets. 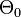 is the first ordinal onto which the continuum cannot be mapped by an ordinal-definable surjection (see Θ (set theory)).
is the first ordinal onto which the continuum cannot be mapped by an ordinal-definable surjection (see Θ (set theory)).
Shelah proved that if the existence of a Woodin cardinal is consistent then it is consistent that the nonstationary ideal on ω1 is  -saturated.
Woodin also proved the equiconsistency of the existence of infinitely many Woodin cardinals and the existence of an
-saturated.
Woodin also proved the equiconsistency of the existence of infinitely many Woodin cardinals and the existence of an 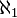 -dense ideal over
-dense ideal over 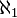 .
.
Hyper-Woodin cardinals
A cardinal κ is called hyper-Woodin if there exists a normal measure U on κ such that for every set S, the set
- {λ < κ | λ is <κ-S-strong}
is in U.
λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary embedding
- j : V → N
with
- λ = crit(j),
- j(λ)≥ δ, and
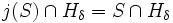 .
.
The name alludes to the classical result that a cardinal is Woodin if and only if for every set S, the set
- {λ < κ | λ is <κ-S-strong}
is a stationary set
The measure U will contain the set of all Shelah cardinals below κ.
Weakly hyper-Woodin cardinals
A cardinal κ is called weakly hyper-Woodin if for every set S there exists a normal measure U on κ such that the set {λ < κ | λ is <κ-S-strong} is in U. λ is <κ-S-strong if and only if for each δ < κ there is a transitive class N and an elementary
embedding j : V → N with λ = crit(j), j(λ) >= δ, and 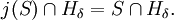
The name alludes to the classic result that a cardinal is Woodin if for every set S, the set {λ < κ | λ is <κ-S-strong} is stationary.
The difference between hyper-Woodin cardinals and weakly hyper-Woodin cardinals is that the choice of U does not depend on the choice of the set S for hyper-Woodin cardinals.
Notes and references
Further reading
- Kanamori, Akihiro (2003). The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings (2nd ed.). Springer. ISBN 3-540-00384-3.
- For proofs of the two results listed in consequences see Handbook of Set Theory (Eds. Foreman, Kanamori, Magidor) (to appear). Drafts of some chapters are available.
- Ernest Schimmerling, Woodin cardinals, Shelah cardinals and the Mitchell-Steel core model, Proceedings of the American Mathematical Society 130/11, pp. 3385–3391, 2002, online
- Steel, John R. (October 2007). "What is a Woodin Cardinal?" (PDF). Notices of the American Mathematical Society 54 (9): 1146–7. Retrieved 2008-01-15.