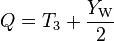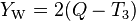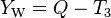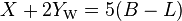Weak hypercharge

Flavour in particle physics
Flavour quantum numbers
Isospin: I or I₃ Charm: C Strangeness: S Topness: T Bottomness: B′
Related quantum numbers
Baryon number: B Lepton number: L Weak isospin: T or T₃ Electric charge: Q X-charge: X
Combinations
Hypercharge: Y Y = (B + S + C + B′ + T) Y = 2 (Q − I₃) Weak hypercharge: Y_W Y_W = 2 (Q − T₃) X + 2Y_W = 5 (B − L)
Flavour mixing
CKM matrix PMNS matrix Flavour complementarity

The weak hypercharge in particle physics is a quantum number relating the electric charge and the third component of weak isospin. It is conserved (only terms that are overall weak-hypercharge neutral are allowed in the Lagrangian) and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions (which is not conserved in weak interactions). It is frequently denoted Y_W and corresponds to the gauge symmetry U(1).^[1]

Definition

Weak hypercharge is the generator of the U(1) component of the electroweak gauge group, SU(2)×U(1) and its associated quantum field B mixes with the W³ electroweak quantum field to produce the observed Z gauge boson and the photon of quantum electrodynamics.

Weak hypercharge, usually written as Y_W, satisfies the equality:

\qquad Q = T_3 + {Y_{\rm W} \over 2}

where Q is the electrical charge (in elementary charge units) and T₃ is the third component of weak isospin. Rearranging, the weak hypercharge can be explicitly defined as:

\qquad Y_{\rm W} = 2(Q - T_3)

	left-handed	el. charge Q	weak isospin T₃	weak hyper- charge Y_W	right-handed	el. charge Q	weak isospin T₃	weak hyper- charge Y_W
Leptons	ν e, ν μ, ν τ	0	+1/2	−1	Do not interact (if exist at all)
Leptons	e−, μ−, τ−	−1	−1/2	−1	e− R, μ− R, τ− R	−1	0	−2
Quarks	u, c, t	+2/3	+1/2	+1/3	u R, c R, t R	+2/3	0	+4/3
Quarks	d, s, b	−1/3	−1/2	+1/3	d R, s R, b R	−1/3	0	−2/3

Note: sometimes weak hypercharge is scaled so that

\qquad Y_{\rm W} = Q - T_3

although this is a minority usage.^[2]

Hypercharge assignments in the Standard Model are determined up to a twofold ambiguity by demanding cancellation of all anomalies.

Baryon and lepton number

Weak hypercharge is related to baryon number minus lepton number via:

X + 2Y_{\rm W} = 5(B - L) \,

where X is a GUT-associated conserved quantum number. Since weak hypercharge is always conserved this implies that baryon number minus lepton number is also always conserved, within the Standard Model and most extensions.

Neutron decay

n → p + e− + ν
e

Hence neutron decay conserves baryon number B and lepton number L separately, so also the difference B − L is conserved.

Proton decay

Proton decay is a prediction of many grand unification theories.

p+ → e+ + π0 → e+ + 2γ

Hence proton decay conserves B − L, even though it violates both lepton number and baryon number conservation.

Notes

↑ J. F. Donoghue, E. Golowich, B. R. Holstein (1994). Dynamics of the standard model. Cambridge University Press. p. 52. ISBN 0-521-47652-6.
↑ M. R. Anderson (2003). The mathematical theory of cosmic strings. CRC Press. p. 12. ISBN 0-7503-0160-0.

This article is issued from Wikipedia - version of the Thursday, September 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.