Weak Büchi automaton

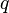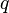In computer science and automata theory, a Weak Büchi automaton is a formalism which represents a set of infinite words. A Weak Büchi automaton is a modification of Büchi automaton such that for all pair of states $q$ and $q'$ belonging to the same strongly connected component, $q$ is accepting if and only if $q'$ is accepting.

A Büchi automaton accepts a word $w$ if there exists a run, such that at least one state occurring infinitely often in the final state set 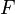$F$ . For Weak Büchi automata, this condition is equivalent to the existence of a run which ultimately stays in the set of accepting states.

Weak Büchi automata are strictly less-expressive than Büchi automaton and than Co-Büchi automaton.

Properties

Weak Büchi automata are equivalent to deterministic Weak Büchi automata. The determinization algorithm runs in exponential time. The deterministic Weak Büchi automata can be minimized in time 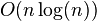$O(n \log(n))$ .

The languages accepted by Weak Büchi automata are closed under union, intersection and complementation.

References

Boigelot, Bernard (3 July 2005). "An effective decision procedure for linear arithmetic over the integers and reals". ACM Transactions on Computational Logic 6 (3): 614–633. doi:10.1145/1071596.1071601.

This article is issued from Wikipedia - version of the Monday, January 25, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.