
Illustration of water retention on a surface.
Water retention on mathematical surfaces refers to the water caught in ponds on a surface of cells of various heights on a regular array such as a square lattice, where water is rained down on every cell in the system. The boundaries of the system are open and allow water to flow out. Water will be trapped in ponds, and eventually all ponds will fill to their maximum height, with any additional water flowing over spillways and out the boundaries of the system. The problem is to find the amount of water trapped or retained for a given surface. This has been studied extensively for two mathematical surfaces: magic squares and random surfaces.
Magic squares

A 5x5 magic square with the maximal retention.
Magic squares have been studied for over 2000 years. In 2007, the idea of studying the water retention on a magic square was proposed.[1] In 2010, Al Zimmermann's programing contest[2] produced the presently known maximum retention values for magic squares order 4 to 28.[3] Computing tools used to investigate and illustrate this problem are found here.[4][5][6]
There are 4,211,744 different retention patterns for the 7x7 square. A combination
of a lake and ponds is best for attaining maximum retention. No known patterns for maximum retention
have an island in a pond or lake.[1]
136 units of retention
| 1 |
34 |
36 |
32 |
31 |
39 |
2 |
| 25 |
20 |
5 |
15 |
14 |
49 |
47 |
| 24 |
12 |
45 |
28 |
16 |
13 |
37 |
| 38 |
9 |
27 |
40 |
29 |
11 |
21 |
| 41 |
8 |
17 |
23 |
46 |
18 |
22 |
| 43 |
48 |
10 |
7 |
6 |
19 |
42 |
| 3 |
44 |
35 |
30 |
33 |
26 |
4 |
|
|
island |
|
spillway |
|
365 units of retention
| 5 |
33 |
44 |
39 |
34 |
18 |
2 |
| 20 |
49 |
8 |
15 |
11 |
48 |
24 |
| 37 |
14 |
23 |
29 |
30 |
6 |
36 |
| 43 |
12 |
22 |
17 |
26 |
10 |
45 |
| 38 |
1 |
27 |
21 |
32 |
16 |
40 |
| 28 |
47 |
9 |
13 |
7 |
46 |
25 |
| 4 |
19 |
42 |
41 |
35 |
31 |
3 |
|
|
lake |
|
405 units of retention
| 4 |
25 |
46 |
19 |
31 |
32 |
18 |
| 27 |
44 |
16 |
45 |
12 |
2 |
29 |
| 47 |
10 |
14 |
6 |
48 |
20 |
30 |
| 21 |
43 |
1 |
42 |
5 |
41 |
22 |
| 33 |
11 |
49 |
3 |
24 |
15 |
40 |
| 34 |
7 |
13 |
37 |
17 |
39 |
28 |
| 9 |
35 |
36 |
23 |
38 |
26 |
8 |
|
|
pond |
|
417 units of retention
| 13 |
30 |
22 |
41 |
39 |
20 |
10 |
| 31 |
15 |
48 |
7 |
4 |
45 |
25 |
| 27 |
44 |
17 |
18 |
21 |
8 |
40 |
| 23 |
42 |
5 |
29 |
9 |
43 |
24 |
| 34 |
1 |
47 |
6 |
49 |
2 |
36 |
| 35 |
11 |
3 |
46 |
16 |
38 |
26 |
| 12 |
32 |
33 |
28 |
37 |
19 |
14 |
|
|
|
best for max retention |
|
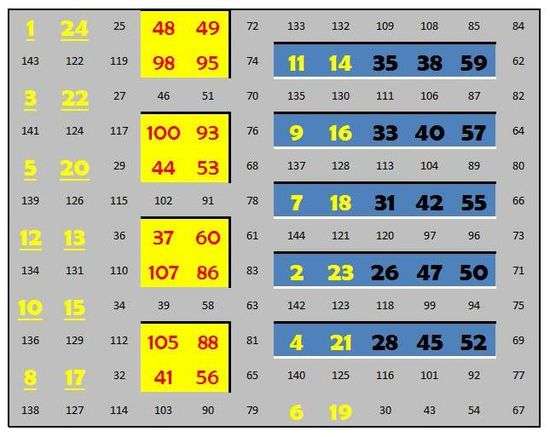
Maximum-retention magic squares for orders 7-9 are shown below:[3]
418 units of retention
| 2 | 22 | 38 | 40 | 39 | 19 | 15 |
| 29 | 45 | 13 | 12 | 4 | 44 | 28 |
| 42 | 17 | 20 | 21 | 26 | 8 | 41 |
| 25 | 46 | 10 | 18 | 6 | 43 | 27 |
| 32 | 3 | 49 | 7 | 48 | 1 | 35 |
| 31 | 9 | 11 | 47 | 16 | 37 | 24 |
| 14 | 33 | 34 | 30 | 36 | 23 | 5 |
| Hermann Jurksch April 6, 2010 |
|
797 units of retention
| 1 | 26 | 41 | 39 | 50 | 47 | 40 | 16 |
| 36 | 43 | 21 | 61 | 9 | 7 | 51 | 32 |
| 42 | 6 | 62 | 15 | 57 | 25 | 5 | 48 |
| 29 | 58 | 14 | 23 | 27 | 56 | 4 | 49 |
| 52 | 13 | 20 | 33 | 22 | 18 | 64 | 38 |
| 53 | 17 | 35 | 24 | 8 | 60 | 19 | 44 |
| 37 | 63 | 12 | 11 | 59 | 2 | 46 | 30 |
| 10 | 34 | 55 | 54 | 28 | 45 | 31 | 3 |
| Hermann Jurksch April 5, 2010 |
|
1,408 units of retention
| 1 | 37 | 57 | 47 | 66 | 50 | 53 | 55 | 3 |
| 43 | 59 | 11 | 77 | 25 | 75 | 10 | 15 | 54 |
| 58 | 7 | 78 | 21 | 34 | 22 | 81 | 12 | 56 |
| 45 | 73 | 14 | 23 | 32 | 30 | 27 | 74 | 51 |
| 69 | 17 | 39 | 28 | 52 | 36 | 35 | 26 | 67 |
| 44 | 72 | 18 | 38 | 42 | 13 | 20 | 76 | 46 |
| 64 | 6 | 80 | 16 | 31 | 24 | 79 | 8 | 61 |
| 40 | 65 | 9 | 70 | 19 | 71 | 4 | 62 | 29 |
| 5 | 33 | 63 | 49 | 68 | 48 | 60 | 41 | 2 |
| Walter Trump June 12, 2010 |
|
The figures below show the 10x10 magic square. Is it possible to look at the
patterns above and predict what the pattern for maximum retention for
the 10x10 square will be? No theory has been developed that
can predict the correct combination of lake and ponds for all orders, however some principles do apply.
The first color-coded figure
shows a design principle of how the largest available numbers are placed around
the lake and ponds. The second and third figures
show promising patterns that were tried but did not achieve
maximum retention.[1]
2267 units of retention
| 1 |
41 |
79 |
58 |
75 |
63 |
64 |
68 |
52 |
4 |
| 47 |
80 |
5 |
81 |
8 |
90 |
87 |
6 |
76 |
25 |
| 78 |
7 |
35 |
23 |
97 |
44 |
36 |
100 |
13 |
72 |
| 60 |
82 |
19 |
91 |
39 |
29 |
27 |
14 |
93 |
51 |
| 73 |
21 |
98 |
32 |
40 |
48 |
33 |
59 |
16 |
85 |
| 65 |
89 |
46 |
26 |
50 |
62 |
34 |
30 |
20 |
83 |
| 56 |
88 |
43 |
28 |
31 |
37 |
22 |
42 |
92 |
66 |
| 70 |
11 |
99 |
17 |
55 |
38 |
45 |
94 |
9 |
67 |
| 53 |
71 |
12 |
95 |
24 |
10 |
96 |
18 |
77 |
49' |
| 2 |
15 |
69 |
54 |
86 |
84 |
61 |
74 |
57 |
3 |
| color key: |
|
> |
|
> |
|
> |
|
> |
|
|
|
2251 units of retention
| 1 | 50 | 66 | 46 | 86 | 54 | 77 | 74 | 48 | 3 |
| 53 | 68 | 17 | 97 | 32 | 91 | 25 | 4 | 78 | 40 |
| 67 | 13 | 98 | 28 | 35 | 24 | 96 | 52 | 16 | 76 |
| 58 | 93 | 15 | 41 | 36 | 21 | 51 | 92 | 23 | 75 |
| 85 | 30 | 29 | 34 | 45 | 64 | 37 | 26 | 99 | 56 |
| 55 | 95 | 10 | 31 | 63 | 44 | 22 | 89 | 14 | 82 |
| 71 | 20 | 90 | 60 | 33 | 27 | 100 | 7 | 18 | 79 |
| 70 | 6 | 59 | 88 | 19 | 87 | 8 | 38 | 83 | 47 |
| 43 | 73 | 72 | 11 | 94 | 12 | 9 | 84 | 65 | 42 |
| 2 | 57 | 49 | 69 | 62 | 81 | 80 | 39 | 61 | 5 |
|
2228 units of retention
| 1 | 45 | 79 | 53 | 87 | 83 | 55 | 72 | 27 | 3 |
| 51 | 80 | 20 | 95 | 11 | 40 | 89 | 14 | 74 | 31 |
| 78 | 19 | 90 | 42 | 15 | 56 | 33 | 94 | 5 | 73 |
| 48 | 97 | 30 | 9 | 64 | 26 | 36 | 43 | 91 | 41 |
| 85 | 28 | 54 | 22 | 68 | 57 | 61 | 23 | 25 | 82 |
| 86 | 13 | 39 | 62 | 21 | 52 | 46 | 60 | 38 | 88 |
| 66 | 99 | 10 | 49 | 59 | 32 | 12 | 24 | 96 | 58 |
| 70 | 9 | 98 | 6 | 34 | 67 | 17 | 92 | 37 | 75 |
| 18 | 71 | 16 | 100 | 65 | 8 | 93 | 7 | 77 | 50 |
| 2 | 44 | 69 | 47 | 81 | 84 | 63 | 76 | 35 | 4 |
|
Several orders have more than one pattern for maximum retention. The figure below shows the two patterns for the 11x11 magic square with the apparent maximum retention of 3,492 units:[3]
Pattern #1
| 1 | 55 | 81 | 69 | 103 | 47 | 83 | 64 | 99 | 67 | 2 |
| 59 | 89 | 13 | 106 | 17 | 111 | 18 | 102 | 8 | 100 | 48 |
| 82 | 14 | 119 | 36 | 45 | 53 | 117 | 19 | 76 | 12 | 98 |
| 73 | 107 | 31 | 43 | 46 | 23 | 37 | 112 | 30 | 101 | 68 |
| 104 | 20 | 56 | 61 | 54 | 60 | 52 | 38 | 121 | 21 | 84 |
| 105 | 27 | 25 | 50 | 80 | 70 | 66 | 16 | 49 | 108 | 75 |
| 74 | 109 | 35 | 39 | 78 | 58 | 41 | 22 | 120 | 5 | 90 |
| 86 | 10 | 115 | 57 | 34 | 28 | 40 | 114 | 26 | 96 | 65 |
| 77 | 91 | 33 | 116 | 29 | 32 | 118 | 24 | 42 | 15 | 94 |
| 6 | 87 | 92 | 9 | 113 | 110 | 11 | 97 | 7 | 95 | 44 |
| 4 | 62 | 71 | 85 | 72 | 79 | 88 | 63 | 93 | 51 | 3 |
|
Pattern #2
| 1 | 36 | 97 | 69 | 86 | 74 | 64 | 89 | 90 | 62 | 3 |
| 68 | 99 | 10 | 101 | 8 | 108 | 109 | 12 | 11 | 92 | 53 |
| 98 | 5 | 31 | 15 | 118 | 28 | 58 | 116 | 61 | 91 | 50 |
| 77 | 100 | 21 | 113 | 22 | 29 | 35 | 66 | 117 | 9 | 82 |
| 87 | 6 | 121 | 32 | 51 | 41 | 72 | 39 | 38 | 114 | 70 |
| 79 | 105 | 46 | 33 | 52 | 71 | 60 | 47 | 49 | 25 | 104 |
| 75 | 106 | 54 | 23 | 81 | 55 | 56 | 45 | 48 | 26 | 102 |
| 88 | 7 | 120 | 67 | 42 | 40 | 63 | 43 | 34 | 110 | 57 |
| 76 | 96 | 59 | 107 | 27 | 30 | 37 | 24 | 119 | 13 | 83 |
| 18 | 95 | 19 | 17 | 111 | 115 | 14 | 112 | 20 | 85 | 65 |
| 4 | 16 | 93 | 94 | 73 | 80 | 103 | 78 | 84 | 44 | 2 |
|
The most-perfect magic squares require all 2x2 cell blocks to have the same sum. ( a few examples flagged with yellow background, red font).
Increased internal complexity reduces retention.[7]
Before 2010 if you wanted an example of a magic square larger than 5x5 you had to follow clever construction rules that provided very isolated examples. The 13x13 pandiagonal magic square below is such an example. Harry White's CompleteSquare Utility [4] allows anyone to use the magic square as a potter would use a lump of clay. The second image shows a 14x14 magic square that was molded to form ponds that write the 1514 - 2014 dates. The animation notes how the surface was sculptured to fill all ponds to capacity before the water flows off the square. This square honors the 500th anniversary of Durer's famous magic square in Melencolia I.
The figure below is a 15x15 bordered magic square with zero water retention.[4]
This figure also provides an example of a square and its complement that have the same pattern of retention.
There are 137 order 4 and 3,254,798 order 5 magic squares that do not retain water.[1]
| 212 |
198 |
200 |
202 |
204 |
206 |
208 |
13 |
12 |
10 |
8 |
6 |
4 |
2 |
210 |
| 27 |
186 |
174 |
176 |
178 |
180 |
182 |
39 |
38 |
36 |
34 |
32 |
30 |
184 |
199 |
| 25 |
51 |
164 |
154 |
156 |
158 |
160 |
61 |
60 |
58 |
56 |
54 |
162 |
175 |
201 |
| 23 |
49 |
71 |
146 |
138 |
140 |
142 |
79 |
78 |
76 |
74 |
144 |
155 |
177 |
203 |
| 21 |
47 |
69 |
87 |
132 |
126 |
128 |
93 |
92 |
90 |
130 |
139 |
157 |
179 |
205 |
| 19 |
45 |
67 |
85 |
99 |
122 |
118 |
103 |
102 |
120 |
127 |
141 |
159 |
181 |
207 |
| 17 |
43 |
65 |
83 |
97 |
107 |
116 |
109 |
114 |
119 |
129 |
143 |
161 |
183 |
209 |
| 15 |
41 |
63 |
81 |
95 |
105 |
111 |
113 |
115 |
121 |
131 |
145 |
163 |
185 |
211 |
| 215 |
189 |
167 |
149 |
135 |
125 |
112 |
117 |
110 |
101 |
91 |
77 |
59 |
37 |
11 |
| 217 |
191 |
169 |
151 |
137 |
106 |
108 |
123 |
124 |
104 |
89 |
75 |
57 |
35 |
9 |
| 219 |
193 |
171 |
153 |
96 |
100 |
98 |
133 |
134 |
136 |
94 |
73 |
55 |
33 |
7 |
| 221 |
195 |
173 |
82 |
88 |
86 |
84 |
147 |
148 |
150 |
152 |
80 |
53 |
31 |
5 |
| 223 |
197 |
64 |
72 |
70 |
68 |
66 |
165 |
166 |
168 |
170 |
172 |
62 |
29 |
3 |
| 225 |
42 |
52 |
50 |
48 |
46 |
44 |
187 |
188 |
190 |
192 |
194 |
196 |
40 |
1 |
| 16 |
28 |
26 |
24 |
22 |
20 |
18 |
213 |
214 |
216 |
218 |
220 |
222 |
224 |
14 |
|
16 x 16 associative magic square retaining 17840 units. The lake in the first image looks a little uglier than common. Jarek Wroblewski notes that good patterns for maximum retention will have equal or near equal number of retaining cells on each peripheral edge ( in this case 7 cells on each edge) [2] The second image is doctored, shading in the top and bottom 37 values.
The figure below is a 17x17 Luo-Shu format magic square.[8]
The Luo-Shu format construction method seems to produce a maximum number of ponds. The drainage path for the cell in green is long eventually
spilling off the square at the yellow spillway cell.
The figure to the right shows what information can be derived from looking at the actual water content for each cell.
Only the 144 values are highlighted to keep the square from looking too busy.
Focusing on the green cell with a base value 7, the highest obstruction on the path out is its neighbor cell
with the value of 151 (151-7=144 units retained). Water rained into this cell exits the square at the yellow 10 cell.
| 137 | 282 | 121 | 266 | 105 | 250 | 89 | 234 | 73 | 218 | 57 | 202 | 41 | 186 | 25 | 170 | 9 |
| 10 | 138 | 283 | 122 | 267 | 106 | 251 | 90 | 235 | 74 | 219 | 58 | 203 | 42 | 187 | 26 | 154 |
| 155 | 11 | 139 | 284 | 123 | 268 | 107 | 252 | 91 | 236 | 75 | 220 | 59 | 204 | 43 | 171 | 27 |
| 28 | 156 | 12 | 140 | 285 | 124 | 269 | 108 | 253 | 92 | 237 | 76 | 221 | 60 | 188 | 44 | 172 |
| 173 | 29 | 157 | 13 | 141 | 286 | 125 | 270 | 109 | 254 | 93 | 238 | 77 | 205 | 61 | 189 | 45 |
| 46 | 174 | 30 | 158 | 14 | 142 | 287 | 126 | 271 | 110 | 255 | 94 | 222 | 78 | 206 | 62 | 190 |
| 191 | 47 | 175 | 31 | 159 | 15 | 143 | 288 | 127 | 272 | 111 | 239 | 95 | 223 | 79 | 207 | 63 |
| 64 | 192 | 48 | 176 | 32 | 160 | 16 | 144 | 289 | 128 | 256 | 112 | 240 | 96 | 224 | 80 | 208 |
| 209 | 65 | 193 | 49 | 177 | 33 | 161 | 17 | 145 | 273 | 129 | 257 | 113 | 241 | 97 | 225 | 81 |
| 82 | 210 | 66 | 194 | 50 | 178 | 34 | 162 | 1 | 146 | 274 | 130 | 258 | 114 | 242 | 98 | 226 |
| 227 | 83 | 211 | 67 | 195 | 51 | 179 | 18 | 163 | 2 | 147 | 275 | 131 | 259 | 115 | 243 | 99 |
| 100 | 228 | 84 | 212 | 68 | 196 | 35 | 180 | 19 | 164 | 3 | 148 | 276 | 132 | 260 | 116 | 244 |
| 245 | 101 | 229 | 85 | 213 | 52 | 197 | 36 | 181 | 20 | 165 | 4 | 149 | 277 | 133 | 261 | 117 |
| 118 | 246 | 102 | 230 | 69 | 214 | 53 | 198 | 37 | 182 | 21 | 166 | 5 | 150 | 278 | 134 | 262 |
| 263 | 119 | 247 | 86 | 231 | 70 | 215 | 54 | 199 | 38 | 183 | 22 | 167 | 6 | 151 | 279 | 135 |
| 136 | 264 | 103 | 248 | 87 | 232 | 71 | 216 | 55 | 200 | 39 | 184 | 23 | 168 | 7 | 152 | 280 |
| 281 | 120 | 265 | 104 | 249 | 88 | 233 | 72 | 217 | 56 | 201 | 40 | 185 | 24 | 169 | 8 | 153 |
|
| 00 | | | | | | | | | | | | | | | | |
| | | | 144 | | 144 | | 144 | | 144 | | 144 | | 144 | | 128 | |
| | 127 | | | 144 | | 144 | | 144 | | 144 | | 144 | | 128 | | |
| | | 127 | | | 144 | | 144 | | 144 | | 144 | | 128 | | 127 | |
| | 127 | | 127 | | | 144 | | 144 | | 144 | | 128 | | 127 | | |
| | | 127 | | 127 | | | 144 | | 144 | | 128 | | 127 | | 127 | |
| | 127 | | 127 | | 127 | | | 144 | | 128 | | 127 | | 127 | | |
| | | 127 | | 127 | | 127 | | | 128 | | 127 | | 127 | | 127 | |
| | 127 | | 127 | | 127 | | 127 | | | 127 | | 127 | | 127 | | |
| | | 127 | | 127 | | 127 | | 144 | | | 127 | | 127 | | 127 | |
| | 127 | | 127 | | 127 | | 144 | | 144 | | | 127 | | 127 | | |
| | | 127 | | 127 | | 144 | | 144 | | 144 | | | 127 | | 127 | |
| | 127 | | 127 | | 144 | | 144 | | 144 | | 144 | | | 127 | | |
| | | 127 | | 144 | | 144 | | 144 | | 144 | | 144 | | | 127 | |
| | 127 | | 144 | | 144 | | 144 | | 144 | | 144 | | 144 | | | |
| | | 144 | | 144 | | 144 | | 144 | | 144 | | 144 | | 144 | | |
| 00 | | | | | | | | | | | | | | | | |
|
The computer age now allows for the exploration of the physical properties of magic squares of any order. The figure below shows the largest magic square studied in the contest. For L > 20 the number of variables/ equations increases to the point where it makes the pattern for maximum retention predictable.
L = 28: 219822 units of retention
| 1 | 5 | 259 | 659 | 257 | 713 | 712 | 282 | 256 | 283 | 657 | 255 | 656 | 284 | 726 | 725 | 254 | 285 | 654 | 253 | 286 | 55 | 673 | 674 | 471 | 645 | 7 | 3 |
| 9 | 640 | 664 | 25 | 717 | 26 | 27 | 716 | 715 | 714 | 28 | 668 | 29 | 744 | 30 | 31 | 730 | 743 | 50 | 681 | 680 | 679 | 51 | 52 | 678 | 206 | 646 | 11 |
| 265 | 665 | 355 | 722 | 496 | 618 | 71 | 484 | 95 | 121 | 721 | 400 | 774 | 418 | 130 | 176 | 293 | 541 | 749 | 479 | 106 | 175 | 389 | 148 | 230 | 682 | 43 | 644 |
| 663 | 14 | 724 | 356 | 313 | 513 | 75 | 189 | 198 | 449 | 213 | 775 | 87 | 478 | 539 | 139 | 326 | 60 | 451 | 750 | 461 | 566 | 141 | 442 | 638 | 477 | 677 | 276 |
| 266 | 720 | 164 | 572 | 354 | 226 | 491 | 171 | 512 | 117 | 776 | 247 | 244 | 503 | 435 | 85 | 629 | 406 | 144 | 634 | 751 | 592 | 462 | 125 | 134 | 514 | 44 | 672 |
| 711 | 15 | 565 | 116 | 100 | 357 | 579 | 112 | 637 | 777 | 108 | 469 | 433 | 546 | 80 | 559 | 525 | 468 | 526 | 227 | 146 | 752 | 368 | 557 | 328 | 212 | 46 | 671 |
| 710 | 16 | 153 | 174 | 222 | 119 | 353 | 627 | 778 | 64 | 297 | 456 | 544 | 474 | 178 | 473 | 410 | 563 | 515 | 331 | 403 | 387 | 753 | 402 | 569 | 304 | 45 | 670 |
| 709 | 17 | 70 | 325 | 168 | 509 | 445 | 779 | 166 | 366 | 401 | 83 | 92 | 482 | 129 | 338 | 408 | 492 | 585 | 529 | 369 | 298 | 424 | 754 | 582 | 519 | 676 | 275 |
| 267 | 719 | 156 | 103 | 455 | 531 | 780 | 391 | 358 | 537 | 76 | 142 | 367 | 309 | 522 | 245 | 320 | 437 | 632 | 386 | 545 | 497 | 224 | 123 | 755 | 161 | 675 | 277 |
| 264 | 718 | 444 | 600 | 508 | 781 | 196 | 553 | 65 | 352 | 488 | 344 | 624 | 104 | 216 | 551 | 98 | 616 | 370 | 294 | 233 | 101 | 416 | 490 | 109 | 756 | 47 | 652 |
| 662 | 18 | 723 | 417 | 782 | 310 | 564 | 606 | 420 | 483 | 359 | 518 | 548 | 246 | 475 | 58 | 628 | 385 | 571 | 69 | 149 | 223 | 335 | 235 | 86 | 113 | 733 | 274 |
| 263 | 669 | 218 | 783 | 127 | 429 | 581 | 77 | 399 | 136 | 88 | 351 | 602 | 538 | 636 | 635 | 371 | 220 | 74 | 570 | 99 | 633 | 543 | 498 | 502 | 173 | 48 | 727 |
| 661 | 19 | 784 | 407 | 179 | 184 | 195 | 609 | 393 | 495 | 203 | 567 | 360 | 576 | 394 | 384 | 388 | 137 | 625 | 154 | 523 | 229 | 489 | 485 | 219 | 314 | 738 | 279 |
| 268 | 748 | 597 | 307 | 505 | 615 | 441 | 315 | 583 | 562 | 194 | 542 | 446 | 350 | 372 | 588 | 316 | 443 | 120 | 162 | 89 | 102 | 560 | 317 | 110 | 329 | 737 | 272 |
| 729 | 20 | 521 | 177 | 232 | 340 | 128 | 411 | 152 | 122 | 334 | 241 | 605 | 383 | 361 | 412 | 578 | 202 | 619 | 73 | 611 | 549 | 589 | 587 | 432 | 568 | 736 | 278 |
| 262 | 746 | 68 | 580 | 242 | 187 | 558 | 183 | 398 | 601 | 594 | 182 | 373 | 296 | 460 | 349 | 332 | 556 | 205 | 419 | 614 | 323 | 547 | 586 | 207 | 114 | 735 | 273 |
| 269 | 745 | 458 | 131 | 111 | 78 | 337 | 610 | 532 | 612 | 622 | 382 | 59 | 365 | 554 | 448 | 362 | 613 | 82 | 574 | 172 | 493 | 466 | 126 | 145 | 630 | 734 | 280 |
| 261 | 747 | 158 | 465 | 598 | 221 | 459 | 214 | 524 | 167 | 374 | 608 | 533 | 409 | 319 | 330 | 595 | 348 | 181 | 428 | 305 | 453 | 584 | 199 | 61 | 765 | 33 | 651 |
| 660 | 21 | 773 | 536 | 561 | 94 | 345 | 165 | 204 | 381 | 621 | 528 | 447 | 211 | 500 | 135 | 452 | 342 | 363 | 301 | 396 | 527 | 185 | 225 | 764 | 306 | 666 | 281 |
| 270 | 694 | 517 | 772 | 392 | 431 | 312 | 240 | 375 | 190 | 617 | 151 | 91 | 324 | 333 | 520 | 231 | 215 | 511 | 347 | 540 | 238 | 97 | 763 | 413 | 707 | 49 | 650 |
| 260 | 693 | 105 | 405 | 771 | 550 | 295 | 380 | 302 | 336 | 311 | 620 | 234 | 133 | 427 | 197 | 516 | 150 | 90 | 607 | 364 | 425 | 762 | 486 | 67 | 530 | 703 | 271 |
| 53 | 692 | 300 | 163 | 631 | 770 | 376 | 191 | 157 | 552 | 414 | 415 | 555 | 422 | 626 | 590 | 339 | 507 | 79 | 188 | 147 | 761 | 430 | 308 | 436 | 132 | 702 | 54 |
| 683 | 22 | 397 | 423 | 535 | 379 | 769 | 155 | 421 | 494 | 322 | 454 | 390 | 217 | 510 | 623 | 107 | 200 | 591 | 186 | 760 | 341 | 346 | 593 | 237 | 115 | 24 | 696 |
| 684 | 23 | 228 | 118 | 377 | 575 | 303 | 768 | 327 | 534 | 487 | 573 | 438 | 472 | 457 | 599 | 464 | 439 | 143 | 759 | 604 | 138 | 160 | 72 | 395 | 124 | 32 | 697 |
| 480 | 691 | 209 | 378 | 440 | 504 | 140 | 501 | 767 | 81 | 201 | 159 | 404 | 210 | 467 | 577 | 57 | 169 | 758 | 193 | 426 | 470 | 93 | 596 | 639 | 180 | 701 | 499 |
| 648 | 258 | 695 | 299 | 192 | 208 | 481 | 321 | 318 | 766 | 463 | 96 | 63 | 506 | 84 | 236 | 239 | 757 | 343 | 708 | 450 | 243 | 170 | 434 | 603 | 706 | 62 | 641 |
| 10 | 649 | 38 | 690 | 39 | 37 | 689 | 688 | 687 | 40 | 732 | 36 | 742 | 741 | 740 | 739 | 731 | 41 | 667 | 35 | 705 | 42 | 34 | 13 | 704 | 66 | 643 | 12 |
| 2 | 6 | 647 | 287 | 686 | 685 | 288 | 252 | 251 | 658 | 289 | 728 | 250 | 249 | 290 | 248 | 291 | 655 | 292 | 653 | 56 | 698 | 699 | 700 | 476 | 642 | 8 | 4 |
| Jarek Wroblewski March 24, 2010 |
2014 brought the ability to write a unlimited amount of text on the mathematical surface of a magic square.[1][4]
Random surfaces

Water retention on a random surface of 10 levels.
Another system in which the retention question has been studied is a surface of random heights. Here one can map the random surface to site percolation, and each cell is mapped to a site on the underlying graph or lattice that represents the system. Using percolation theory, one can explain many properties of this system. It is an example of the invasion percolation model in which fluid is introduced in the system from any random site.[9][10][11]
In hydrology, one is concerned with runoff and formation of catchments.[12] The boundary between different drainage basin (watersheds in North America) forms a drainage divide with a fractal dimension of about 1.22.[13]
[14]
[15]
The retention problem can be mapped to standard percolation.[16][17][18]
For a system of five equally probable levels, for example, the amount of water stored R5 is just the sum of the water stored in two-level systems R2(p) with varying fractions of levels p in the lowest state:
- R5 = R2(1/5) + R2(2/5) + R2(3/5) + R2(4/5)
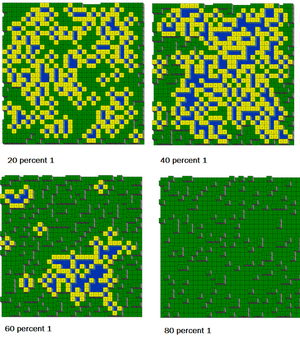
Typical two-level systems 1,2 with p = 0.2, 0.4, 0.6, 0.8 are shown on the right (blue: wet, green: dry, yellow: spillways bordering wet sites). The net retention of a five-level system is the sum of all these. The top level traps no water because it is far above the percolation threshold for a square lattice, 0.592746.
The retention of a two-level system R2(p) is the amount of water connected to ponds that do not touch the boundary of the system. When p is above the critical percolation threshold p c, there will be a percolating cluster or pond that visits the entire system. The probability that a point belongs to the percolating or "infinite" cluster is written as P∞ in percolation theory, and it is related to R2(p) by R2(p)/L2 = p − P∞ where L is the size of the square. Thus, the retention of a multilevel system can be related to a well-known quantity in percolation theory.
To measure the retention, one can use a flooding algorithm in which water is introduced from the boundaries and floods through the lowest spillway as the level is raised. The retention is just the difference in the water level that a site was flooded minus the height of the terrain below it.
Besides the systems of discrete levels described above, one can make the terrain variable a continuous variable say from 0 to 1. Likewise, one can make the surface height itself be a continuous function of the spatial variables. In all cases, the basic concept of the mapping to an appropriate percolation system remains.
A curious result is that a square system of n discrete levels can retain more water than a system of n+1 levels, for sufficiently large order L > L*. This behavior can be understood through percolation theory, which can also be used to estimate L* ≈ (p - pc)-ν where ν = 4/3, p = i*/n where i* is the largest value of i such that i/n < pc, and pc = 0.592746 is the site percolation threshold for a square lattice. Numerical simulations give the following values of L*, which are extrapolated to non-integer values. For example, R2 < R3 for L ≤ 51, but R2 > R3 for L ≥ 52:[16]
| n |
n+1 |
L* |
Retention at L* |
|---|
| 2 |
3 |
51.12 |
790 |
| 4 |
5 |
198.1 |
26000 |
| 7 |
8 |
440.3 |
246300 |
| 9 |
10 |
559.1 |
502000 |
| 12 |
13 |
1390.6 |
428850 |
| 14 |
15 |
1016.3 |
2607000 |
As n gets larger, crossing become less and less frequent, and the value of L* where crossing occurs is no longer a monotonic function of n.
The retention when the surface is not entirely random but correlated with a Hurst exponent H is discussed in.[18]
Algorithms
The following time line shows the application of different algorithms that have expanded the size of the square that can be evaluated for retention
2007 Define all neighbor-avoiding walks from each interior cell to the exterior and then sort all those paths for the least obstruction or cell value. The least obstruction value minus the interior cell value provides the water retention for that interior cell (negative values are set to a retention value of 0). The number of neighbor-avoiding walks to be evaluated grows exponentially with the square size and thus limits this methodology to L < 6.[1]
2009 Flooding algorithm - water is introduced from the boundaries and floods through the lowest spillway as the level is raised. The retention is just the difference in the water level that a site was flooded minus the height of the terrain below it. The flooding algorithm allows for the evaluation of water retention up to L < 10,000.[16] This algorithm is similar to Meyer's flooding algorithm that has been used in analysis of topographical surfaces.
2011 With the realization that an n-level system can be broken down into a collection of two-level systems with varying probabilities, standard percolation algorithms can be used to find the retention as simply the total number of sites at the lower level minus the draining regions (clusters of low-level sites touching the boundary). A novel application of the Hoshen-Kopelman algorithm in which both rows and columns are added one at a time allows L to be very large (up to 109), but computing time considerations limits L to the order of 107.[19]
Paths that drain water off the square, used in the neighbor-avoiding walk algorithm
The panel below from left to right shows: 1) the three unique interior positions for the 5x5 square; 2 & 4) correct paths off the square in grey for the interior corner cell in red; 3) incorrect path in grey as the water cannot travel on the diagonals; 5) this path is correct but there is a short-circuit possible between the grey cells. Neighbor-avoiding walks define the unique or non-redundant paths that drain water off the square.
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 1 | |
|
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
|
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
|
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
|
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
| 00 | 00 | 00 | 00 | 00 | |
|
See also
References
- 1 2 3 4 5 6 Craig Knecht, http://www.knechtmagicsquare.paulscomputing.com
- 1 2 Al Zimmermann http://www.azspcs.net/Contest/MagicWater/FinalReport
- 1 2 3 Harvey Heinz, http://www.magic-squares.net/square-update-2.htm#Knecht
- 1 2 3 4 Harry White, http://users.eastlink.ca/~sharrywhite/Download.html
- ↑ Walter Trump http://www.trump.de/magic-squares/
- ↑ Johan Ofverstedt,http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-176018
- ↑ Harry White, http://users.eastlink.ca/~sharrywhite/Most-perfect.html
- ↑ Harvey Heinz,http://www.magic-squares.net/square-update.htm
- ↑ Chayes, J. T.; L. Chayes; C. M. Newman (1985). "The stochastic geometry of invasion percolation". Communications in Mathematical Physics 101 (3): 383–407. Bibcode:1985CMaPh.101..383C. doi:10.1007/BF01216096.
- ↑ Damron, Michael; Artëm Sapozhnikov; Bálint Vágvölgyi (2009). "Relations between invasion percolation and critical percolation in two dimensions". Annals of Probability 37 (6): 2297–2331. doi:10.1214/09-AOP462.
- ↑ van den Berg, Jacob; Antal Járai; Bálint Vágvölgyi (2007). "The size of a pond in 2D invasion percolation". Electron. Comm. In Probab. 12: 411–420. doi:10.1214/ECP.v12-1327.
- ↑ Tetzlaff, D.; McDonnell, J. J.; Uhlenbrook, S.; McGuire, K. J.; Bogaart, P. W.; Naef, F.; Baird, A. J.; Dunn, S. M.; Soulsby, C. (2011). "Conceptualizing catchment processes: simply too complex?". Hydrological Processes 22 (11): 1099–1085. Bibcode:2008HyPr...22.1727T. doi:10.1002/hyp.7069.
- ↑ Fehr, E.; D. Kadau, N. A. M. Araújo, J. S. Andrade Jr., and H. J. Herrmann (2011). "Scaling Relations for Watersheds". Physical Review E 84 (3): 036116. arXiv:1106.6200. Bibcode:2011PhRvE..84c6116F. doi:10.1103/PhysRevE.84.036116.
- ↑ Schrenk, K. J.; N. A. M. Araújo, J. S. Andrade Jr., and H. J. Herrmann (2012). "Fracturing Ranked Surfaces". Scientific Reports 2: 348. arXiv:1103.3256. Bibcode:2012NatSR...2E.348S. doi:10.1038/srep00348.
- ↑ Fehr, E.; D. Kadau, J. S. Andrade Jr., and H. J. Herrmann (2011). "Impact of Perturbations on Watersheds". Physical Review Letters 106 (4): 048501. arXiv:1101.5890. Bibcode:2011PhRvL.106d8501F. doi:10.1103/PhysRevLett.106.048501.
- 1 2 3 Knecht, Craig; Walter Trump; Daniel ben-Avraham; Robert M. Ziff (2012). "Retention capacity of random surfaces". Physical Review Letters 108 (4): 045703. arXiv:1110.6166. Bibcode:2012PhRvL.108d5703K. doi:10.1103/PhysRevLett.108.045703.
- ↑ Baek, Seung Ki; Beom Jun Kim (2012). "Critical Condition of the Water-Retention Model". Physical Review E 85: 032103. arXiv:1111.0425. Bibcode:2012PhRvE..85c2103B. doi:10.1103/PhysRevE.85.032103.
- 1 2 Schrenk, K. J.; N. A. M Araújo; R. M. Ziff; H. J. Herrmann (2014). "Retention capacity of correlated surfaces". arXiv:1403.2082.
- ↑ Hoshen, Joseph (1998). "On the application of the enhanced Hoshen-Kopelman algorithm for image analysis". Pattern Recognition Letters 19 (7). doi:10.1016/S0167-8655(98)00018-x.
Further reading
- Pickover, Clifford (2002). The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures Across Dimensions. Princeton, NJ: Princeton University Press. ISBN 0-691-11597-4.
- Stauffer, Dietrich; Aharony, A. (1994). Introduction to Percolation Theory. London Bristol, PA: Taylor & Francis. ISBN 978-0-7484-0253-3.
External links














 A201126 with links to magic square pictures
A201126 with links to magic square pictures A201127
A201127