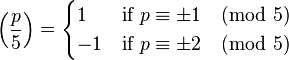Wall–Sun–Sun prime
| Named after | Donald Dines Wall, Zhi Hong Sun and Zhi Wei Sun |
|---|---|
| Publication year | 1992 |
| Number of known terms | 0 |
| Conjectured number of terms | Infinite |
In number theory, a Wall–Sun–Sun prime or Fibonacci–Wieferich prime is a certain kind of prime number which is conjectured to exist, although none are known.
Definition
A prime p ≠ 2, 5 is called a Wall–Sun–Sun prime if p2 divides the Fibonacci number 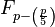 , where the Legendre symbol
, where the Legendre symbol 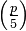 has the values
has the values
Equivalently, a prime p is a Wall–Sun–Sun prime if Lp ≡ 1 (mod p2), where Lp is the p-th Lucas number.[1]:42
Existence
| | Unsolved problem in mathematics: Are there any Wall–Sun–Sun primes? If yes, are there an infinite number of them? (more unsolved problems in mathematics) |
Originally, Donald Dines Wall hypothesized the non-existence of Fibonacci Wieferich primes, but could not prove they were impossible, hence the question remains open. It has since been conjectured that there are infinitely many Wall–Sun–Sun primes.[2] No Wall–Sun–Sun primes are known as of October 2014.
In 2007, Richard J. McIntosh and Eric L. Roettger showed that if any exist, they must be > 2×1014.[3] Dorais and Klyve extended this range to 9.7×1014 without finding such a prime.[4] In December 2011, another search was started by the PrimeGrid project.[5] As of October 2014, PrimeGrid has extended the search limit to 2.8×1016 and continues.[6]
History
Wall–Sun–Sun primes are named after Donald Dines Wall,[7] Zhi Hong Sun and Zhi Wei Sun; Z. H. Sun and Z. W. Sun showed in 1992 that if the first case of Fermat's last theorem was false for a certain prime p, then p would have to be a Wall–Sun–Sun prime.[8] As a result, prior to Andrew Wiles' proof of Fermat's last theorem, the search for Wall–Sun–Sun primes was also the search for a potential counterexample to this centuries-old conjecture.
Generalizations
A k-Wall–Sun–Sun prime is defined as a prime p such that p2 divides the k-Fibonacci number (a Lucas sequence Un with (P, Q) = (k, −1)) 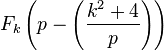 , where
, where 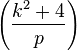 is the Legendre symbol. For example, 241 is a k-Wall–Sun–Sun prime for k = 3. Thus, a prime p is a k-Wall–Sun–Sun prime iff Vk(p) ≡ 1 (mod p2), where Vn is a Lucas sequence with (P, Q) = (k, −1).
Least n-Wall–Sun–Sun prime are
is the Legendre symbol. For example, 241 is a k-Wall–Sun–Sun prime for k = 3. Thus, a prime p is a k-Wall–Sun–Sun prime iff Vk(p) ≡ 1 (mod p2), where Vn is a Lucas sequence with (P, Q) = (k, −1).
Least n-Wall–Sun–Sun prime are
- 13, 241, 2, 3, 191, 5, 2, 3, 2683, ... (start with n = 2)
A Tribonacci–Wieferich prime is a prime p satisfying h(p) = h(p2), where h is the least positive integer satisfying [Th,Th+1,Th+2] ≡ [T0, T1, T2] (mod m) and Tn denotes the n-th Tribonacci number. No Tribonacci–Wieferich prime exists below 1011.[9]
A Pell–Wieferich prime is a prime p satisfying p2 divides Pp−1, when p congruent to 1 or 7 (mod 8), or p2 divides Pp+1, when p congruent to 3 or 5 (mod 8), where Pn denotes the n-th Pell number. For example, 13, 31, and 1546463 are Pell–Wieferich primes, and no others below 109. (sequence A238736 in OEIS) In fact, Pell–Wieferich primes are 2-Wall–Sun–Sun primes.
Near-Wall–Sun–Sun primes
A prime p such that 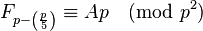 with small |A| is called near-Wall–Sun–Sun prime.[10] Near-Wall–Sun–Sun primes with A = 0 would be Wall–Sun–Sun primes.
with small |A| is called near-Wall–Sun–Sun prime.[10] Near-Wall–Sun–Sun primes with A = 0 would be Wall–Sun–Sun primes.
Wall–Sun–Sun primes with discriminant D
It is in the field 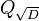 with discriminant D.
In the original Wall–Sun–Sun prime case, D = 5, more generalized, a Lucas–Wieferich prime to (P, Q) is a Wieferich prime to base Q and a Wall–Sun–Sun prime with discriminant D = P2 + 4Q.[11]
with discriminant D.
In the original Wall–Sun–Sun prime case, D = 5, more generalized, a Lucas–Wieferich prime to (P, Q) is a Wieferich prime to base Q and a Wall–Sun–Sun prime with discriminant D = P2 + 4Q.[11]
In this definition, a generalized Wall–Sun–Sun prime p should be odd and not divide D. It's a conjecture that for every natural number D, there are infinitely many Wall–Sun–Sun primes with discriminant D.
| D | Wall–Sun–Sun primes with discriminant D | OEIS sequence |
| 1 | 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (All odd primes) | A065091 |
| 2 | 13, 31, 1546463, ... | A238736 |
| 3 | 103, 2297860813, ... | A238490 |
| 4 | 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (All odd primes) | |
| 5 | ... | |
| 6 | 7, 523, ... | |
| 7 | ... | |
| 8 | 13, 31, 1546463, ... | |
| 9 | 5, 7, 11, 13, 17, 19, 23, 29, ... (All odd primes except 3) | |
| 10 | 191, 643, 134339, 25233137, ... | |
| 11 | ... | |
| 12 | 103, 2297860813, ... | |
| 13 | 241, ... | |
| 14 | 6707879, 93140353, ... | |
| 15 | 181, 1039, 2917, 2401457, ... | |
| 16 | 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (All odd primes) | |
| 17 | ... | |
| 18 | 13, 31, 1546463, ... | |
| 19 | 79, 1271731, 13599893, 31352389, ... | |
| 20 | ... | |
| 21 | 46179311, ... | |
| 22 | 43, 73, 409, 28477, ... | |
| 23 | 7, 733, ... | |
| 24 | 7, 523, ... | |
| 25 | 3, 7, 11, 13, 17, 19, 23, 29, ... (All odd primes except 5) | |
| 26 | 2683, 3967, 18587, ... | |
| 27 | 103, 2297860813, ... | |
| 28 | ... | |
| 29 | 3, 11, ... | |
| 30 | ... |
See also
- Wieferich prime
- Wolstenholme prime
- Wilson prime
- PrimeGrid
- Fibonacci prime
- Pisano period
- Table of congruences
References
- ↑ Andrejić, V. (2006). "On Fibonacci powers" (PDF). Univ. Beograd Publ. Elektrotehn. Fak. Ser. Mat. 17: 38–44. doi:10.2298/PETF0617038A.
- ↑ Klaška, Jiří (2007), "Short remark on Fibonacci−Wieferich primes", Acta Mathematica Universitatis Ostraviensis 15 (1): 21–25.
- ↑ McIntosh, R. J.; Roettger, E. L. (2007). "A search for Fibonacci−Wieferich and Wolstenholme primes" (PDF). Mathematics of Computation 76 (260): 2087–2094. doi:10.1090/S0025-5718-07-01955-2.
- ↑ Dorais, F. G.; Klyve, D. W. (2010). "Near Wieferich primes up to 6.7 × 1015" (PDF).
- ↑ Wall–Sun–Sun Prime Search project at PrimeGrid
- ↑ Wall–Sun–Sun Prime Search statistics at PrimeGrid
- ↑ Wall, D. D. (1960), "Fibonacci Series Modulo m", American Mathematical Monthly 67 (6): 525–532, doi:10.2307/2309169
- ↑ Sun, Zhi-Hong; Sun, Zhi-Wei (1992), "Fibonacci numbers and Fermat’s last theorem" (PDF), Acta Arithmetica 60 (4): 371–388
- ↑ Klaška, Jiří (2008). "A search for Tribonacci–Wieferich primes". Acta Mathematica Universitatis Ostraviensis 16 (1): 15–20.
- ↑ McIntosh, R. J.; Roettger, E. L. (2007), "A search for Fibonacci–Wieferich and Wolstenholme primes", Mathematics of Computation (AMS) 76 (260): 2087–2094, doi:10.1090/S0025-5718-07-01955-2, archived from the original (PDF) on 2010-12-10
- ↑ The Fibonacci sequence modulo p2
Further reading
- Crandall, Richard E.; Pomerance, Carl (2001). Prime Numbers: A Computational Perspective. Springer. p. 29. ISBN 0-387-94777-9.
- Saha, Arpan; Karthik, C. S. (2011). "A Few Equivalences of Wall–Sun–Sun Prime Conjecture". Working paper. arXiv:1102.1636.
External links
- Chris Caldwell, The Prime Glossary: Wall–Sun–Sun prime at the Prime Pages.
- Weisstein, Eric W., "Wall–Sun–Sun prime", MathWorld.
- Richard McIntosh, Status of the search for Wall–Sun–Sun primes (October 2003)
| ||||||||||||||||||||||||||||||||||||||||||||||