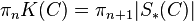Waldhausen S-construction
In mathematics, specifically in algebraic K-theory, the Waldhausen S-construction produces from a Waldhausen category C a sequence of Kan complexes 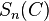 , which forms a spectrum. Let
, which forms a spectrum. Let 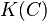 denote the loop space of the geometric realization
denote the loop space of the geometric realization 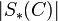 of
of 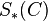 . Then the group
. Then the group
is the n-th K-grouo of C. Thus, it gives a way to define higher K-groups. Another approach for higher K-theory is Quillen's Q-construction.
The construction is due to Friedhelm Waldhausen.
See also
References
- F. Waldhausen, Algebraic K-theory of spaces, Alg. and Geo. Top., Springer Lect. Notes Math. 1126 (1985), 318-419, pdf.
- Lurie, J., Higher K-Theory of ∞-Categories (Lecture 16)
External links
This article is issued from Wikipedia - version of the Monday, January 25, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.