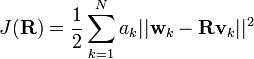Wahba's problem

In applied mathematics, Wahba's problem, first posed by Grace Wahba in 1965, seeks to find a rotation matrix (special orthogonal matrix) between two coordinate systems from a set of (weighted) vector observations. Solutions to Wahba's problem are often used in satellite attitude determination utilising sensors such as magnetometers and multi-antenna GPS receivers. The cost function that Wahba's problem seeks to minimise is as follows:

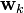J(\mathbf{R}) = \frac{1}{2} \sum_{k=1}^{N} a_k|| \mathbf{w}_k - \mathbf{R} \mathbf{v}_k ||^2

where $\mathbf{w}_k$ is the k-th 3-vector measurement in the reference frame, 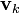$\mathbf{v}_k$ is the corresponding k-th 3-vector measurement in the body frame and 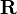$\mathbf{R}$ is a 3 by 3 rotation matrix between the coordinate frames. $a_k$ is an optional set of weights for each observation.

A number of solutions to the problem have appeared in literature, notably Davenport's q-method, QUEST and singular value decomposition-based methods.

Solution by Singular Value Decomposition

One solution can be found using a singular value decomposition as reported by Markley

1. Obtain a matrix 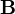$\mathbf{B}$ as follows:

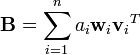
$\mathbf{B} = \sum_{i=1}^{n} a_i \mathbf{w}_i {\mathbf{v}_i}^T$

2. Find the singular value decomposition of 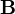$\mathbf{B}$

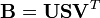
$\mathbf{B} = \mathbf{U} \mathbf{S} \mathbf{V}^T$

3. The rotation matrix is simply:

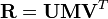
$\mathbf{R} = \mathbf{U} \mathbf{M} \mathbf{V}^T$

where 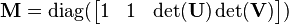$\mathbf{M} = \operatorname{diag}(\begin{bmatrix} 1 & 1 & \det(\mathbf{U}) \det(\mathbf{V})\end{bmatrix})$

References

Markley, F. L. Attitude Determination using Vector Observations and the Singular Value Decomposition Journal of the Astronautical Sciences, 1988, 38, 245-258

Wahba, G. Problem 65–1: A Least Squares Estimate of Spacecraft Attitude, SIAM Review, 1965, 7(3), 409

Wahba's problem

Solution by Singular Value Decomposition

References

See also