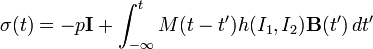Wagner model

Wagner model is a rheological model developed for the prediction of the viscoelastic properties of polymers. It might be considered as a simplified practical form of the Bernstein-Kearsley-Zapas model. The model was developed by German rheologist Manfred Wagner.

For the isothermal conditions the model can be written as:

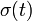\mathbf{\sigma}(t) = -p \mathbf{I} + \int_{-\infty}^{t} M(t-t')h(I_1,I_2)\mathbf{B}(t')\, dt'

where:

$\mathbf{\sigma}(t)$ is the Cauchy stress tensor as function of time t,
p is the pressure
$\mathbf{I}$ is the unity tensor
M is the memory function showing, usually expressed as a sum of exponential terms for each mode of relaxation:

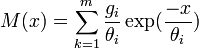M(x)=\sum_{k=1}^m \frac{g_i}{\theta_i}\exp(\frac{-x}{\theta_i})

, where for each mode of the relaxation,

g_i

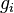is the relaxation modulus and

\theta_i

is the relaxation time;

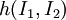$h(I_1,I_2)$ is the strain damping function that depends upon the first and second invariants of Finger tensor $\mathbf{B}$ .

The strain damping function is usually written as:

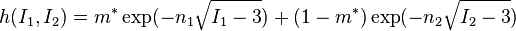h(I_1,I_2)=m^*\exp(-n_1 \sqrt{I_1-3})+(1-m^*)\exp(-n_2 \sqrt{I_2-3})

The strain hardening function equal to one, then the deformation is small and approaching zero, then the deformations are large.

The Wagner equation can be used in the non-isothermal cases by applying time-temperature shift factor.

References

M.H. Wagner Rheologica Acta, v.15, 136 (1976)
M.H. Wagner Rheologica Acta, v.16, 43, (1977)
B. Fan, D. Kazmer, W. Bushko, Polymer Engineering and Science, v44, N4 (2004)

This article is issued from Wikipedia - version of the Thursday, April 02, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.