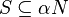Bounded set (topological vector space)
In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set. Conversely a set that is not bounded is called unbounded.
Bounded sets are a natural way to define a locally convex polar topologies on the vector spaces in a dual pair, as the polar of a bounded set is an absolutely convex and absorbing set. The concept was first introduced by John von Neumann and Andrey Kolmogorov in 1935.
Definition
Given a topological vector space (X,τ) over a field F, S is called bounded if for every neighborhood N of the zero vector there exists a scalar α such that
with
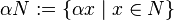 .
.
This is equivalent[1] to the condition that S is absorbed by every neighborhood of the zero vector, i.e., that for all neighborhoods N, there exists t such that
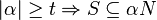 .
.
In locally convex topological vector spaces the topology τ of the space can be specified by a family P of semi-norms. An equivalent characterization of bounded sets in this case is, a set S in (X,P) is bounded if and only if it is bounded for all semi normed spaces (X,p) with p a semi norm of P.
Examples and nonexamples
- Every finite set of points is bounded
- The set of points of a Cauchy sequence is bounded, the set of points of a Cauchy net need not to be bounded.
- Every relatively compact set in a topological vector space is bounded. If the space is equipped with the weak topology the converse is also true.
- A (non null) subspace of a Hausdorff topological vector space is not bounded
Properties
- The closure of a bounded set is bounded.
- In a locally convex space, the convex envelope of a bounded set is bounded. (Without local convexity this is false, as the
 spaces for
spaces for  have no nontrivial open convex subsets.)
have no nontrivial open convex subsets.) - The finite union or finite sum of bounded sets is bounded.
- Continuous linear mappings between topological vector spaces preserve boundedness.
- A locally convex space is seminormable if and only if there exists a bounded neighbourhood of zero.
- The polar of a bounded set is an absolutely convex and absorbing set.
- A set A is bounded if and only if every countable subset of A is bounded
Generalization
The definition of bounded sets can be generalized to topological modules. A subset A of a topological module M over a topological ring R is bounded if for any neighborhood N of 0M there exists a neighborhood w of 0R such that w A ⊂ N.
See also
Notes
- ↑ Schaefer 1970, p. 25.
References
- Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics 53. Cambridge University Press. pp. 44–46.
- H.H. Schaefer (1970). Topological Vector Spaces. GTM 3. Springer-Verlag. pp. 25–26. ISBN 0-387-05380-8.
| ||||||||||||||||||||||||||||||||||