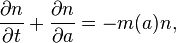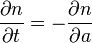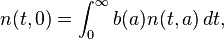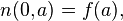Von Foerster equation (ecology)
The von Foerster equation is a linear first-order partial differential equation encountered in several areas of mathematical biology – for example, cell proliferation modeling; it is applied when age structure is an important feature in the mathematical model.[1] It was presented by biophysics professor Heinz von Foerster.
Mathematical formula
The mathematical formula can be derived from first principles. It reads:
where: n = n(t,a), t stands for time and a for age. m(a) is the death in function of the population age; n(t,a) is the population density in function of age.
When m(a) = 0, we have:[1]
It relates that a population ages, and that fact is the only one that influences change in population density; the negative sign shows that time flows in just one direction, that there is no birth and the population is going to die out.
Analytical solution
The von Foerster equation is a transport equation; it can be solved using a characteristics method.[1] Another way is by similarity solution; and a third is a numerical approach such as finite differences.
To get the solution, the following boundary conditions should be added:
which states that the initial births should be conserved (see Sharpe–Lotka–McKendrick’s equation for otherwise), and that
which states that the initial population must be given; then it will evolve according to the partial differential equation.
Similar equations
In Sebastian Anita, Viorel Arnautu, Vincenzo Capasso. An Introduction to Optimal Control Problems in Life Sciences and Economics (Birkhouser. 2011), this equation appears as a special case of the Sharpe–Lotka–McKendrick’s equation; in the latter there is inflow, and the math is based on directional derivative.