Volume hologram

Volume holograms are holograms where the thickness of the recording material is much larger than the light wavelength used for recording. In this case diffraction of light from the hologram is possible only as Bragg diffraction, i.e., the light has to have the right wavelength (color) and the wave must have the right shape (beam direction, wavefront profile). Volume holograms are also called thick holograms or Bragg holograms.

Theory

Volume holograms were first treated by H. Kogelnik in 1969 ^[1] by the so-called "coupled-wave theory". For volume phase holograms it is possible to diffract 100% of the incoming reference light into the signal wave, i.e., full diffraction of light can be achieved. Volume absorption holograms show much lower efficiencies. H. Kogelnik provides analytical solutions for transmission as well as for reflection conditions. A good text-book description of the theory of volume holograms can be found in a book from J. Goodman .^[2]

Manufacturing

A volume hologram is usually made by exposing a photo-thermo-refractive glass to an interference pattern from an ultraviolet laser. It is also possible to make volume holograms in nonphotosensitive glass by exposing it to femtosecond laser pulses ^[3]

Bragg selectivity

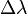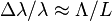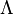In the case of a simple Bragg reflector the wavelength selectivity $\Delta\lambda$ can be roughly estimated by $\Delta\lambda/\lambda \approx \Lambda/L$ , where $\lambda$ is the vacuum wavelength of the reading light, $\Lambda$ is the period length of the grating and $L$ is the thickness of the grating. The assumption is just that the grating is not too strong, i.e., that the full length of the grating is used for light diffraction. 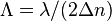Considering that because of the Bragg condition the simple relation $\Lambda=\lambda/(2\Delta n)$ holds, where 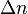$\Delta n$ is the modulated refractive index in the material (not the base index) at this wavelength, one sees that for typical values ( 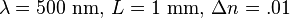$\lambda = 500\mbox{ nm},\, L = 1\mbox{ mm},\, \Delta n = .01$ ) one gets
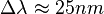$\Delta\lambda \approx 25 nm$ showing the extraordinary wavelength selectivity of such volume holograms.

In the case of a simple grating in the transmission geometry the angular selectivity 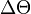$\Delta\Theta$ can be estimated as well: 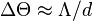$\Delta\Theta \approx \Lambda/d$ , where 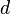$d$ is the thickness of the holographic grating. Here 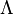$\Lambda$ is given by 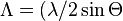$\Lambda = (\lambda/2\sin\Theta$ ). Using again typical numbers ( 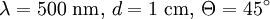$\lambda = 500\mbox{ nm},\, d = 1\mbox{ cm},\, \Theta = 45 ^\circ$ ) one ends up with
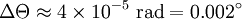$\Delta\Theta \approx 4 \times 10^{-5}\mbox{ rad} = 0.002^\circ$ showing the impressive angular selectivity of volume holograms.

Applications of volume holograms

The Bragg selectivity makes volume holograms very important. Prominent examples are:

Distributed feedback lasers (DFB lasers) as well as distributed Bragg reflector lasers (DBR lasers) where the wavelength selectivity of volume holograms is used to narrow the spectral emission of semiconductor lasers.
Holographic memory devices for holographic data storage where the Bragg selectivity is used to multiplex several holograms in one piece of holographic recording material using effectively the third dimension of the storage material.
Fiber Bragg gratings that employ volume holographic gratings encrypted into an optical fiber.
Wavelength filters that are used as an external feedback in particular for semiconductor lasers.^[4]^[5]^[6] Although the idea is similar to that of DBR lasers, these filters are not integrated onto the chip. With the help of such filters also high-power laser diodes become narrow-band and less temperature sensitive.
Imaging spectroscopy can be achieved by selecting a single wavelength for each pixel in a full camera field.^[7] Volume holograms are used as tunable optical filters to produce monochromatic images, also known as hyperspectral imaging.

Footnotes

↑ H. Kogelnik (1969). "Coupled-wave theory for thick hologram gratings". Bell System Technical Journal 48: 2909. doi:10.1002/j.1538-7305.1969.tb01198.x.
↑ J. Goodman (2005). Introduction to Fourier optics. Roberts & Co Publishers.
↑ Richter, D. and Voigtlander, C. and Becker, R. and Thomas, Jens and Tunnermann, Andreas and Nolte, S. (2011). "Efficient volume Bragg gratings in various transparent materials induced by femtosecond laser pulses". Lasers and Electro-Optics Europe (CLEO EUROPE/EQEC), 2011 Conference on and 12th European Quantum Electronics Conference. pp. 1–1. doi:10.1109/CLEOE.2011.5943325. ISBN 978-1-4577-0533-5.
↑ http://www.ondaxinc.com/ - Ondax, Inc.
↑ http://www.pdld.com/index.htm - PD LD, Inc.
↑ http://www.optigrate.com/ - Optigrate
↑ Blais-Ouellette S., Daigle O., Taylor K., The imaging Bragg Tunable Filter: a new path to integral field spectroscopy and narrow band imaging. Full text here

This article is issued from Wikipedia - version of the Friday, January 22, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.