Vertical vector field
In differential geometry, a vertical vector field is a vector field on a principal G-bundle 
that is in the kernel of 
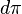at each point of P.[1] More generally, the projection needs only to be a fibered manifold, i.e., a surjective submersion.
See also
Notes
- ↑ Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag, p. 77
References
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag
- Krupka, Demeter; Janyška, Josef (1990), Lectures on differential invariants, Univerzita J. E. Purkyně V Brně, ISBN 80-210-0165-8
- Saunders, D.J. (1989), The geometry of jet bundles, Cambridge University Press, ISBN 0-521-36948-7
This article is issued from Wikipedia - version of the Sunday, January 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.