Supersymmetric gauge theory

In theoretical physics, one often analyzes theories with supersymmetry which also have internal gauge symmetries. So, it is important to come up with a supersymmetric generalization of gauge theories.

We begin this article with a brief introduction to gauge theory. Then we will see what happens when gauge theories are formulated in the framework of supersymmetry (SUSY).

Gauge theory

A gauge theory is a mathematical framework for analysing gauge symmetries. There are two types of symmetries, viz., global and local. A global symmetry is the symmetry which remains invariant at each point of a manifold (manifold can be either of space-time coordinates or that of internal quantum numbers). A local symmetry is the symmetry which depends upon the space over which it is defined, and changes with the variation in coordinates. Thus such symmetry is invariant only locally (i.e., on a subset of the manifold).

Maxwell's equations and quantum electrodynamics are famous examples of gauge theories.

SUSY

According to the Particle Physics, there exist two kinds of particles in nature, namely, bosons and fermions. Bosons are integer spin particles. Their characteristic feature is that any amount of these can occupy a single place in space. Thus they are identified with the forces of nature. Fermions are half-integer spin particles. No two of which, bearing the same quantum number can occupy a single position in space-time. Thus they are identified with the matter. This is the reason why SUSY is considered such an ideal candidate for the unification of radiation (boson-mediated forces) and matter.

This mechanism works via an operator 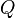$Q$ , known as supersymmetry generator, which acts as follows:

$Q|\text{boson}\rangle = \text{fermion}$
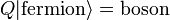
$Q|\text{fermion}\rangle = \text{boson}$

For instance, the supersymmetry generator can take a photon as an argument and transform it into a photino and vice versa. This happens through translation in the (parameter) space. This superspace is a ${\mathbb{Z}_2}$ -graded vector space $\mathcal{W}=\mathcal{W}^0 \oplus \mathcal{W}^1$ , where $\mathcal{W}^0$ is the bosonic Hilbert space and $\mathcal{W}^1$ is the fermionic Hilbert space.

SUSY gauge theory

The motivation for a supersymmetric version of gauge theory can be the fact that gauge invariance is consistent with supersymmetry.

Because both the half-integer spin fermions and the integer spin bosons can become gauge particles. Moreover the vector fields and the spinor fields both reside in the same representation of the internal symmetry group.

Suppose we have a gauge transformation 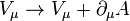$V_{\mu} \rightarrow V_{\mu} + \partial_{\mu} A$ , where $V_{\mu}$ is a vector field and $A$ is the gauge function. The main problem in construction of SUSY Gauge Theory is to extend the above transformation in a way that is consistent with SUSY transformations.

The Wess-Zumino gauge provides a successful solution to this problem. Once such suitable gauge is obtained, the dynamics of the SUSY gauge theory work as follows: we seek a lagrangian that is invariant under the Super-gauge transformations (these transformations are an important tool needed to develop supersymmetric version of a gauge theory). Then we can integrate the lagrangian using the Berezin integration rules and thus obtain the action. Which further leads to the equations of motion and hence can provide a complete analysis of the dynamics of the theory.

$N = 1$ SUSY in 4D (with 4 real generators)

In four dimensions, the minimal $N = 1$ supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates $\theta^1,\theta^2,\bar\theta^1,\bar\theta^2$ , transforming as a two-component spinor and its conjugate.

Every superfield, i.e. a field that depends on all coordinates of the superspace, may be expanded with respect to the new fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfields, that only depend on the variables $θ$ but not their conjugates (more precisely, $\overline{D}f=0$ ). However, a vector superfield depends on all coordinates. It describes a gauge field and its superpartner, namely a Weyl fermion that obeys a Dirac equation.

V = C + i\theta\chi - i \overline{\theta}\overline{\chi} + \tfrac{i}{2}\theta^2(M+iN)-\tfrac{i}{2}\overline{\theta^2}(M-iN) - \theta \sigma^\mu \overline{\theta} v_\mu +i\theta^2 \overline{\theta} \left( \overline{\lambda} + \tfrac{1}{2}\overline{\sigma}^\mu \partial_\mu \chi \right) -i\overline{\theta}^2 \theta \left(\lambda + \tfrac{i}{2}\sigma^\mu \partial_\mu \overline{\chi} \right) + \tfrac{1}{2}\theta^2 \overline{\theta}^2 \left(D + \tfrac{1}{2}\Box C\right)

$V$ is the vector superfield (prepotential) and is real ( $V = V$ ). The fields on the right hand side are component fields.

The gauge transformations act as

V \to V + \Lambda + \overline{\Lambda}

where $Λ$ is any chiral superfield.

It's easy to check that the chiral superfield

W_\alpha \equiv -\tfrac{1}{4}\overline{D}^2 D_\alpha V

is gauge invariant. So is its complex conjugate $\overline{W}_{\dot{\alpha}}$ .

A nonSUSY covariant gauge which is often used is the Wess–Zumino gauge. Here, $C, χ, M$ and $N$ are all set to zero. The residual gauge symmetries are gauge transformations of the traditional bosonic type.

A chiral superfield $X$ with a charge of $q$ transforms as

X \to e^{q\Lambda}X, \qquad \overline{X} \to e^{q\overline{\Lambda}}X

Therefore $X e - qV X$ is gauge invariant. Here $e - qV$ is called a bridge since it "bridges" a field which transforms under $Λ$ only with a field which transforms under $Λ$ only.

More generally, if we have a real gauge group $G$ that we wish to supersymmetrize, we first have to complexify it to $G c \cdot e - qV$ then acts a compensator for the complex gauge transformations in effect absorbing them leaving only the real parts. This is what's being done in the Wess–Zumino gauge.

Differential superforms

Let's rephrase everything to look more like a conventional Yang–Mills gauge theory. We have a $U(1)$ gauge symmetry acting upon full superspace with a 1-superform gauge connection A. In the analytic basis for the tangent space, the covariant derivative is given by $D_M=d_M+iqA_M$ . Integrability conditions for chiral superfields with the chiral constraint

\overline{D}_{\dot{\alpha}}X=0

leave us with

\left\{\overline{D}_{\dot{\alpha}}, \overline{D}_{\dot{\beta}} \right\}=F_{\dot{\alpha}\dot{\beta}}=0.

A similar constraint for antichiral superfields leaves us with $F αβ = 0$ . This means that we can either gauge fix $A_{\dot{\alpha}}=0$ or $A α = 0$ but not both simultaneously. Call the two different gauge fixing schemes I and II respectively. In gauge I, $\overline{d}_{\dot{\alpha}}X=0$ and in gauge II, $d α X = 0$ . Now, the trick is to use two different gauges simultaneously; gauge I for chiral superfields and gauge II for antichiral superfields. In order to bridge between the two different gauges, we need a gauge transformation. Call it $e - V$ (by convention). If we were using one gauge for all fields, $X X$ would be gauge invariant. However, we need to convert gauge I to gauge II, transforming $X$ to $(e - V) q X$ . So, the gauge invariant quantity is $X e - qV X$ .

In gauge I, we still have the residual gauge $e Λ$ where 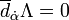$\overline{d}_{\dot{\alpha}}\Lambda=0$ and in gauge II, we have the residual gauge $e Λ$ satisfying $d α Λ = 0$ . Under the residual gauges, the bridge transforms as

e^{-V}\to e^{-\overline{\Lambda}-V-\Lambda}.

Without any additional constraints, the bridge $e - V$ wouldn't give all the information about the gauge field. However, with the additional constraint 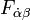$F_{\dot{\alpha}\beta}$ , there's only one unique gauge field which is compatible with the bridge modulo gauge transformations. Now, the bridge gives exactly the same information content as the gauge field.

Theories with 8 or more SUSY generators ( $N > 1$ )

In theories with higher supersymmetry (and perhaps higher dimension), a vector superfield typically describes not only a gauge field and a Weyl fermion but also at least one complex scalar field.

References

Stephen P. Martin. A Supersymmetry Primer, arxiv.org/pdf/hep-ph/9709356v6.pdf .
Prakash, Nirmala. Mathematical Perspective on Theoretical Physics: A Journey from Black Holes to Superstrings, World Scientific (2003).

This article is issued from Wikipedia - version of the Sunday, January 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.