Vector logic
Vector logic[1][2] is an algebraic model of elementary logic based on matrix algebra. Vector logic assumes that the truth values map on vectors, and that the monadic and dyadic operations are executed by matrix operators.
Overview
Classic binary logic is represented by a small set of mathematical functions depending on one (monadic ) or two (dyadic) variables. In the binary set, the value 1 corresponds to true and the value 0 to false. A two-valued vector logic requires a correspondence between the truth-values true (t) and false (f), and two q-dimensional normalized column vectors composed by real numbers s and n, hence:
-
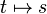 and
and 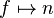
(where 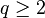 is an arbitrary natural number, and “normalized” means that the length of the vector is 1; usually s and n are orthogonal vectors). This correspondence generates a space of vector truth-values: V2 = {s,n}. The basic logical operations defined using this set of vectors lead to matrix operators.
is an arbitrary natural number, and “normalized” means that the length of the vector is 1; usually s and n are orthogonal vectors). This correspondence generates a space of vector truth-values: V2 = {s,n}. The basic logical operations defined using this set of vectors lead to matrix operators.
The operations of vector logic are based on the scalar product between q-dimensional column vectors: 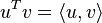 : the orthonormality between vectors s and n implies that
: the orthonormality between vectors s and n implies that 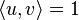 if
if  , and
, and 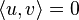 if
if 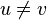 .
.
Monadic operators
The monadic operators result from the application 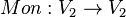 , and the associated matrices have q rows and q columns. The two basic monadic operators for this two-valued vector logic are the identity and the negation:
, and the associated matrices have q rows and q columns. The two basic monadic operators for this two-valued vector logic are the identity and the negation:
- Identity: A logical identity ID(p)is represented by matrix
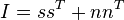 . This matrix operates as follows: Ip = p, p ∈ V2; due to the orthogonality of s respect to n, we have
. This matrix operates as follows: Ip = p, p ∈ V2; due to the orthogonality of s respect to n, we have 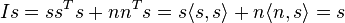 , and conversely
, and conversely 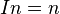 .
.
- Negation: A logical negation ¬p is represented by matrix
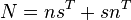 Consequently, Ns = n and Nn = s. The involutory behavior of the logical negation, namely that ¬(¬p) equals p, corresponds with the fact that N2 = I. Is important to note that this vector logic identity matrix is not generally an identity matrix in the sense of matrix algebra.
Consequently, Ns = n and Nn = s. The involutory behavior of the logical negation, namely that ¬(¬p) equals p, corresponds with the fact that N2 = I. Is important to note that this vector logic identity matrix is not generally an identity matrix in the sense of matrix algebra.
Dyadic operators
The 16 two-valued dyadic operators correspond to functions of the type 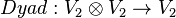 ; the dyadic matrices have q rows and q2 columns.
The matrices that execute these dyadic operations are based on the properties of the Kronecker product.
; the dyadic matrices have q rows and q2 columns.
The matrices that execute these dyadic operations are based on the properties of the Kronecker product.
Two properties of this product are essential for the formalism of vector logic:
- The mixed-product property
If A, B, C and D are matrices of such size that one can form the matrix products AC and BD, then
- Distributive transpose The operation of transposition is distributive over the Kronecker product:
Using these properties, expressions for dyadic logic functions can be obtained:
- Conjunction. The conjunction (p∧q) is executed by a matrix that acts on two vector truth-values:
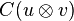 .This matrix reproduces the features of the classical conjunction truth-table in its formulation:
.This matrix reproduces the features of the classical conjunction truth-table in its formulation:
- and verifies
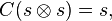 and
and
- Disjunction. The disjunction (p∨q) is executed by the matrix
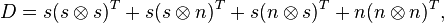 resulting in
resulting in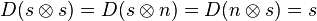 and
and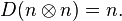
- Implication. The implication corresponds in classical logic to the expression p → q ≡ ¬p ∨ q. The vector logic version of this equivalence leads to a matrix that represents this implication in vector logic:
 . The explicit expression for this implication is:
. The explicit expression for this implication is:
- and the properties of classical implication are satisfied:
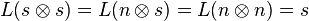 and
and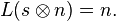
- Equivalence and Exclusive or. In vector logic the equivalence p≡q is represented by the following matrix:
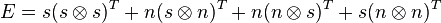 with
with
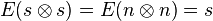 and
and
- The Exclusive or is the negation of the equivalence, ¬(p≡q); it corresponds with the matrix
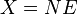 given by
given by
- The Exclusive or is the negation of the equivalence, ¬(p≡q); it corresponds with the matrix
- with
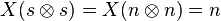 and
and
- with
The matrices S and P correspond to the Sheffer (NAND) and the Peirce (NOR) operations, respectively:
De Morgan's law
In the two-valued logic, the conjunction and the disjunction operations satisfy the De Morgan's law: p∧q≡¬(¬p∨¬q), and its dual: p∨q≡¬(¬p∧¬q)). For the two-valued vector logic this Law is also verified:
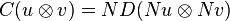 , where u and v are two logic vectors.
, where u and v are two logic vectors.
The Kronecker product implies the following factorization:
Then it can be proved that in the two–dimensional vector logic the De Morgan's law is a law involving operators, and not only a law concerning operations:[3]
Law of contraposition
In the classical propositional calculus, the Law of Contraposition p → q ≡ ¬q → ¬p is proved because the equivalence holds for all the possible combinations of truth-values of p and q.[4] Instead, in vector logic, the law of contraposition emerges from a chain of equalities within the rules of matrix algebra and Kronecker products, as shown in what follows:
This result is based in the fact that D, the disjunction matrix, represents a commutative operation.
Many-valued two-dimensional logic
Many-valued logic was developed by many researchers, particularly by Jan Łukasiewicz and allows extending logical operations to truth-values that include uncertainties.[5] In the case of two-valued vector logic, uncertainties in the truth values can be introduced using vectors with s and n weighted by probabilities.
Let 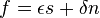 , with
, with ![\epsilon, \delta \in [0,1], \epsilon + \delta = 1](../I/m/72524ae7993eb4a46efad747eb795eac.png) be this kind of “probabilistic” vectors. Here, the many-valued character of the logic is introduced a posteriori via the uncertainties introduced in the inputs.[1]
be this kind of “probabilistic” vectors. Here, the many-valued character of the logic is introduced a posteriori via the uncertainties introduced in the inputs.[1]
Scalar projections of vector outputs
The outputs of this many-valued logic can be projected on scalar functions and generate a particular class of probabilistic logic with similarities with the many-valued logic of Reichenbach.[6][7][8] Given two vectors 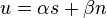 and
and 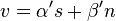 and a dyadic logical matrix
and a dyadic logical matrix  , a scalar probabilistic logic is provided by the projection over vector s:
, a scalar probabilistic logic is provided by the projection over vector s:
Here are the main results of these projections:
The associated negations are:
If the scalar values belong to the set {0, ½, 1}, this many-valued scalar logic is for many of the operators almost identical to the 3-valued logic of Łukasiewicz. Also, it has been proved that when the monadic or dyadic operators act over probabilistic vectors belonging to this set, the output is also an element of this set.[3]
History
The approach has been inspired in neural network models based on the use of high-dimensional matrices and vectors.[9][10] Vector logic is a direct translation into a matrix-vector formalism of the classical Boolean polynomials.[11] This kind of formalism has been applied to develop a fuzzy logic in terms of complex numbers.[12] Other matrix and vector approaches to logical calculus have been developed in the framework of quantum physics, computer science and optics.[13][14][15] Early attempts to use linear algebra to represent logic operations can be referred to Peirce and Copilowish.[16] The Indian biophysicist G.N. Ramachandran developed a formalism using algebraic matrices and vectors to represent many operations of classical Jain Logic known as Syad and Saptbhangi. Indian logic.[17] It requires independent affirmative evidence for each assertion in a proposition, and does not make the assumption for binary complementation.
Boolean polynomials
George Boole established the development of logical operations as polynomials.[11] For the case of monadic operators (such as identity or negation), the Boolean polynomials look as follows:
The four different monadic operations result from the different binary values for the coefficients. Identity operation requires f(1) = 1 and f(0) = 0, and negation occurs if f(1) = 0 and f(0) = 1. For the 16 dyadic operators, the Boolean polynomials are of the form:
The dyadic operations can be translated to this polynomial format when the coefficients f take the values indicated in the respective truth tables. For instance: the NAND operation requires that:
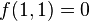 and
and 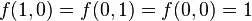 .
.
These Boolean polynomials can be immediately extended to any number of variables, producing a large potential variety of logical operators. In vector logic, the matrix-vector structure of logical operators is an exact translation to the format of liner algebra of these Boolean polynomials, where the x and 1-x correspond to vectors s and n respectively (the same for y and 1-y). In the example of NAND, f(1,1)=n and f(1,0)=f(0,1)=f(0,0)=s and the matrix version becomes:
Extensions
- Vector logic can be extended to include many truth values since large dimensional vector spaces allow to create many orthogonal truth values and the corresponding logical matrices.[2]
- Logical modalities can be fully represented in this context, with recursive process inspired in neural models[2][18]
- Some cognitive problems about logical computations can be analyzed using this formalism, in particular recursive decisions. Any logical expression of classical propositional calculus can be naturally represented by a tree structure.[4] This fact is retained by vector logic, and has been partially used in neural models focused in the investigation of the branched structure of natural languages.[19][20][21][22][23][24]
- The computation via reversible operations as the Fredkin gate can be implemented in vector logic. This implementations provides explicit expressions for matrix operators that produce the input format and the output filtering necessary for obtaining computations[2][3]
- Elementary cellular automata can be analyzed using the operator structure of vector logic; this analysis leads to a spectral decomposition of the laws governing the its dynamics[25][26]
- In addition, based on this formalism, a discrete differential and integral calculus has been developed[27]
See also
References
- 1 2 Mizraji, E. (1992). Vector logics: the matrix-vector representation of logical calculus. Fuzzy Sets and Systems, 50, 179–185, 1992
- 1 2 3 4 Mizraji, E. (2008) Vector logic: a natural algebraic representation of the fundamental logical gates. Journal of Logic and Computation, 18, 97–121, 2008
- 1 2 3 Mizraji, E. (1996) The operators of vector logic. Mathematical Logic Quarterly, 42, 27–39
- 1 2 Suppes, P. (1957) Introduction to Logic, Van Nostrand Reinhold, New York.
- ↑ Łukasiewicz, J. (1980) Selected Works. L. Borkowski, ed., pp. 153–178. North-Holland, Amsterdam, 1980
- ↑ Rescher, N. (1969) Many-Valued Logic. McGraw–Hill, New York
- ↑ Blanché, R. (1968) Introduction à la Logique Contemporaine, Armand Colin, Paris
- ↑ Klir, G.J., Yuan, G. (1995) Fuzzy Sets and Fuzzy Logic. Prentice–Hall, New Jersey
- ↑ Kohonen, T. (1977) Associative Memory: A System-Theoretical Approach. Springer-Verlag, New York
- ↑ Mizraji, E. (1989) Context-dependent associations in linear distributed memories. Bulletin of Mathematical Biology, 50, 195–205
- 1 2 Boole, G. (1854) An Investigation of the Laws of Thought, on which are Founded the Theories of Logic and Probabilities. Macmillan, London, 1854; Dover, New York Reedition, 1958
- ↑ Dick, S. (2005) Towards complex fuzzy logic. IEEE Transactions on Fuzzy Systems, 15,405–414, 2005
- ↑ Mittelstaedt, P. (1968) Philosophische Probleme der Modernen Physik, Bibliographisches Institut, Mannheim
- ↑ Stern, A. (1988) Matrix Logic: Theory and Applications. North-Holland, Amsterdam
- ↑ Westphal, J., Hardy, J. (2005) Logic as a vector system. Journal of Logic and Computation, 15, 751–765
- ↑ Copilowish, I.M. (1948) Matrix development of the calculus of relations. Journal of Symbolic Logic, 13, 193–203
- ↑ Jain, M.K. (2011) Logic of evidence-based inference propositions, Current Science, 1663–1672, 100
- ↑ Mizraji, E. (1994) Modalities in vector logic. Notre Dame Journal of Formal Logic, 35, 272–283
- ↑ Mizraji, E., Lin, J. (2002) The dynamics of logical decisions. Physica D, 168–169, 386–396
- ↑ beim Graben, P., Potthast, R. (2009). Inverse problems in dynamic cognitive modeling. Chaos, 19, 015103
- ↑ beim Graben, P., Pinotsis, D., Saddy, D., Potthast, R. (2008). Language processing with dynamic fields. Cogn. Neurodyn., 2, 79–88
- ↑ beim Graben, P., Gerth, S., Vasishth, S.(2008) Towards dynamical system models of language-related brain potentials. Cogn. Neurodyn., 2, 229–255
- ↑ beim Graben, P., Gerth, S. (2012) Geometric representations for minimalist grammars. Journal of Logic, Language and Information, 21, 393-432 .
- ↑ Binazzi, A.(2012) Cognizione logica e modelli mentali. Studi sulla formazione, 1–2012, pag. 69–84
- ↑ Mizraji, E. (2006) The parts and the whole: inquiring how the interaction of simple subsystems generates complexity. International Journal of General Systems, 35, pp. 395–415.
- ↑ Arruti, C., Mizraji, E. (2006) Hidden potentialities. International Journal of General Systems, 35, 461–469.
- ↑ Mizraji, E. (2015) Differential and integral calculus for logical operations. A matrix–vector approach Journal of Logic and Computation 25, 613-638, 2015
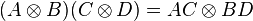
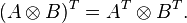
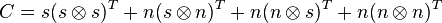
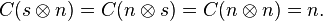

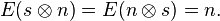
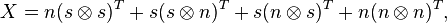
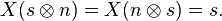
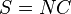
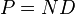
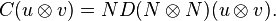
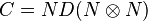
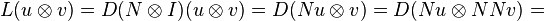

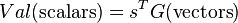
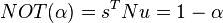
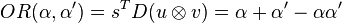
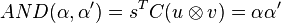
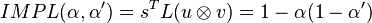
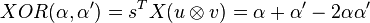
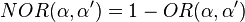
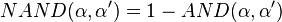
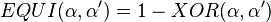
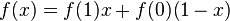
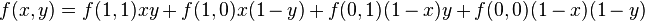
![S=n(s\otimes s)^T + s[(s\otimes n)^T+(n\otimes s)^T+(n\otimes n)^T]](../I/m/dfff7138eb4406f554043258bfbe2e72.png)