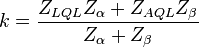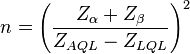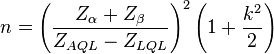Variables sampling plan
A variables sampling plan is an acceptance sampling technique. Plans for variables are intended for quality characteristics that are measured in a continuous scale. This plan requires the knowledge of the statistical model e.g. normal distribution. The historical evolution of this technique dates back to the seminal work of Wallis (1943). The purpose of a plan for variables is to assess whether the process is operating far enough from the specification limit. Plans for variables may produce a similar OC curve to attribute plans with significantly less sample size. The decision criterion of these plans are
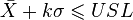 or
or 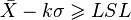
where 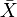 and
and 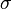 are the sample mean and the standard deviation respectively,
are the sample mean and the standard deviation respectively,  is the critical distance,
is the critical distance, 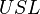 and
and 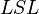 are the upper and lower regulatory limits.
When the above expression is satisfied the proportion nonconforming is lower that expected and therefore the lot is accepted.
are the upper and lower regulatory limits.
When the above expression is satisfied the proportion nonconforming is lower that expected and therefore the lot is accepted.
A variables sampling plan can be designed so that the OC curve passes through two points (AQL, ) and (LQL,
) and (LQL,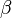 ).
AQL and LQL are the Acceptable quality limit and the limiting quality level respectively.
).
AQL and LQL are the Acceptable quality limit and the limiting quality level respectively.  and
and 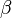 are the producer and consumer’s risks.
The required sample size (
are the producer and consumer’s risks.
The required sample size ( ) and the critical distance (
) and the critical distance ( ) can be obtained as
) can be obtained as
where 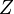 is the normal distribution function.
is the normal distribution function.
When the dispersion is known the required sample size ( ) is obtained from
) is obtained from
while for unknown 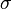 the sample size is approximately
the sample size is approximately
The MIL-STD-414 provides tables to obtain the required sample size and the critical distance according to the type of inspection.
See also
References
- Wallis, W. (1947), Use of variables in acceptance inspection for percent defective. In: Selected Techniques of Statistical Analysis for Scientific and Industrial Research and Production and Management Engineering., Columbia University line feed character in
|title=at position 156 (help)
- MIL-STD-414 (1957), Military Standard. Sampling Procedure and Tables for Inspection by Variables for Percent Defective
Further reading
- Schilling, Edward G.; Neubauer, Dean V. (2010), Acceptance sampling in quality control, CRC Press