Vickrey–Clarke–Groves auction
In auction theory, a Vickrey–Clarke–Groves (VCG) auction is a type of sealed-bid auction of multiple items. Bidders submit bids that report their valuations for the items, without knowing the bids of the other people in the auction. The auction system assigns the items in a socially optimal manner: it charges each individual the harm they cause to other bidders.[1] It also gives bidders an incentive to bid their true valuations, by ensuring that the optimal strategy for each bidder is to bid their true valuations of the items. It is a generalization of a Vickrey auction for multiple items.
The auction is named after William Vickrey,[2] Edward H. Clarke,[3] and Theodore Groves[4] for their papers that successively generalized the idea.
Formal description
- Notation
For any set of auctioned items 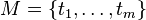 and any set of bidders
and any set of bidders 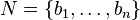 , let
, let 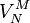 be the social value of the VCG auction for a given bid-combination. For a bidder
be the social value of the VCG auction for a given bid-combination. For a bidder 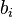 and item
and item 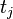 , let the bidder's bid for the item be
, let the bidder's bid for the item be 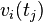 . The notation
. The notation 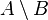 means the set of elements of A which are not elements of B.
means the set of elements of A which are not elements of B.
- Assignment
A bidder 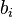 whose bid for an item
whose bid for an item 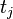 , namely
, namely 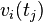 , is an "overbid" wins the item, but pays
, is an "overbid" wins the item, but pays 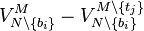 , which is the social cost of his winning that is incurred by the rest of the agents.
, which is the social cost of his winning that is incurred by the rest of the agents.
- Explanation
Indeed, the set of bidders other than 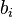 is
is 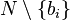 . When item
. When item 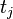 is available, they could attain welfare
is available, they could attain welfare 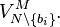 The winning of the item by
The winning of the item by 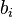 reduces the set of available items to
reduces the set of available items to 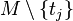 , however, so that the attainable welfare is now
, however, so that the attainable welfare is now 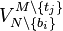 . The difference between the two levels of welfare is therefore the loss in attainable welfare suffered by the rest bidders, as predicted, given the winner
. The difference between the two levels of welfare is therefore the loss in attainable welfare suffered by the rest bidders, as predicted, given the winner 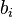 got the item
got the item 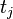 . This quantity depends on the offers of the rest agents and is unknown to agent
. This quantity depends on the offers of the rest agents and is unknown to agent 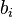 .
.
- Winner's utility
The winning bidder whose bid is his true value  for the item
for the item 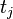 ,
, 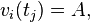 derives maximum utility
derives maximum utility 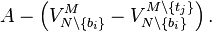
Examples
Example #1
See the example with apples in the Generalization section of Vickrey Auction.
Example #2
Assume that there are two bidders,  and
and  , two items,
, two items, 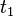 and
and  , and each bidder is allowed to obtain one item. We let
, and each bidder is allowed to obtain one item. We let  be bidder
be bidder 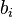 's valuation for item
's valuation for item 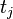 . Assume
. Assume 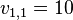 ,
, 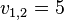 ,
, 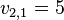 , and
, and 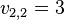 . We see that both
. We see that both  and
and  would prefer to receive item
would prefer to receive item 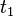 ; however, the socially optimal assignment gives item
; however, the socially optimal assignment gives item 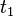 to bidder
to bidder  (so his achieved value is
(so his achieved value is  ) and item
) and item  to bidder
to bidder  (so his achieved value is
(so his achieved value is  ). Hence, the total achieved value is
). Hence, the total achieved value is 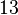 , which is optimal.
, which is optimal.
If person  were not in the auction, person
were not in the auction, person  would still be assigned to
would still be assigned to 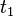 , and hence person
, and hence person  can gain nothing. The current outcome is
can gain nothing. The current outcome is  hence
hence  is charged
is charged 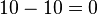 .
.
If person  were not in the auction,
were not in the auction, 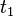 would be assigned to
would be assigned to  , and would have valuation
, and would have valuation 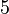 . The current outcome is 3 hence
. The current outcome is 3 hence  is charged
is charged 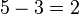 .
.
Example #3
Here we will look at a multiple item auction. Consider the situation when there are  bidders,
bidders,  houses, and values
houses, and values 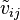 , representing
the value player
, representing
the value player  has for house
has for house 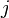 . Possible outcomes in this auction are characterized by bipartite matchings, pairing houses with people.
If we know the values, then maximizing social welfare reduces to computing a maximum weight bipartite matching.
. Possible outcomes in this auction are characterized by bipartite matchings, pairing houses with people.
If we know the values, then maximizing social welfare reduces to computing a maximum weight bipartite matching.
If we do not know the values, then we instead solicit bids 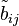 , asking each player
, asking each player  how much he would wish to bid for house
how much he would wish to bid for house 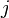 .
Define
.
Define 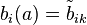 if bidder
if bidder  receives house
receives house  in the matching
in the matching  . Now compute
. Now compute  , a maximum weight
bipartite matching with respect to the bids, and compute
, a maximum weight
bipartite matching with respect to the bids, and compute
-
![p_i = \left[ \max_{a \in A} \sum_{j \neq i} b_j(a) \right] - \sum_{j \neq i} b_j(a^*)](../I/m/64e8c6fca1ba6a2a99b2ba1667664933.png) .
.
The first term is another max weight bipartite matching, and the second term can be computed easily from  .
.
Optimality of Truthful Bidding
The following is a proof that bidding one's true valuations for the auctioned items is optimal.[5]
For each bidder 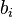 , let
, let  be his true valuation of an item
be his true valuation of an item  , and suppose (without loss of generality) that
, and suppose (without loss of generality) that 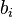 wins
wins  upon submitting his true valuations.
Then the net utility
upon submitting his true valuations.
Then the net utility  attained by
attained by 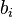 is given by
is given by 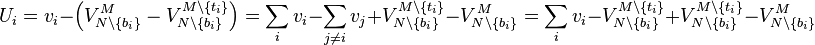
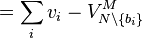 . As
. As 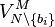 is independent of
is independent of  , the maximization of net utility is pursued by the mechanism along with the maximization of corporate gross utility
, the maximization of net utility is pursued by the mechanism along with the maximization of corporate gross utility 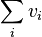 for the declared bid
for the declared bid  .
.
To make it clearer, let us form the difference ![U_i - U_j = \left[v_i + V^{M \setminus \{t_i\}}_{N \setminus \{b_i\}}\right] - \left[v_j + V^{M \setminus \{t_j\}}_{N \setminus \{b_i\}}\right]](../I/m/2c517a2c71202acafe3566690a5a2690.png) between net utility
between net utility  of
of 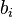 under truthful bidding
under truthful bidding  gotten item
gotten item  , and net utility
, and net utility 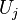 of bidder
of bidder 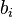 under non-truthful bidding
under non-truthful bidding 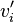 for item
for item  gotten item
gotten item 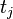 on true utility
on true utility  .
.
![\left[v_j + V^{M \setminus \{t_j\}}_{N \setminus \{b_i\}}\right]](../I/m/e6f9b3dcdd88e7b992f0cf2263f3bec5.png) is the corporate gross utility obtained with the non-truthful bidding. But the allocation assigning
is the corporate gross utility obtained with the non-truthful bidding. But the allocation assigning 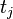 to
to 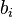 is different from the allocation assigning
is different from the allocation assigning  to
to 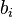 which gets maximum (true) gross corporate utility. Hence
which gets maximum (true) gross corporate utility. Hence ![\left[v_i + V^{M \setminus \{t_i\}}_{N \setminus \{b_i\}}\right] - \left[v_j + V^{M \setminus \{t_j\}}_{N \setminus \{b_i\}}\right]\geq 0](../I/m/a90425e71868f5af587f06bf4e05e300.png) and
and 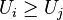 q.e.d.
q.e.d.
See also
- Vickrey–Clarke–Groves mechanism: a generalization of VCG auction. A VCG auction performs a specific task: dividing items among people. A VCG mechanism is more general: it can be used to select any outcome out of a set of possible outcomes.
- Preference revelation
References
- ↑ von Ahn, Luis (2011-10-13). "Sponsored Search" (PDF). 15–396: Science of the Web Course Notes. Carnegie Mellon University. Retrieved 2015-04-13.
- ↑ Vickrey, William (1961). "Counterspeculation, Auctions, and Competitive Sealed Tenders". The Journal of Finance 16 (1): 8–37. doi:10.1111/j.1540-6261.1961.tb02789.x.
- ↑ Clarke, E. (1971). "Multipart Pricing of Public Goods". Public Choice 11 (1): 17–33. doi:10.1007/bf01726210.
- ↑ Groves, T. (1973). "Incentives in Teams". Econometrica 41 (4): 617–631. doi:10.2307/1914085.
- ↑ http://www.cs.cmu.edu/~arielpro/15896/docs/notes14.pdf