Upward planar drawing
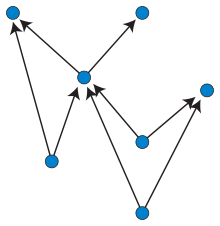
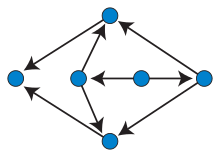
In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint.[1] In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.
Characterizations
A directed acyclic graph must be planar in order to have an upward planar drawing, but not every planar acyclic graph has such a drawing. Among the planar directed acyclic graphs with a single source (vertex with no incoming edges) and sink (vertex with no outgoing edges), the graphs with upward planar drawings are the st-planar graphs, planar graphs in which the source and sink both belong to the same face of at least one of the planar embeddings of the graph. More generally, a graph G has an upward planar drawing if and only if it is directed and acyclic, and is a subgraph of an st-planar graph on the same vertex set.[2]
In an upward embedding, the sets of incoming and outgoing edges incident to each vertex are contiguous in the cyclic ordering of the edges at the vertex. A planar embedding of a given directed acyclic graph is said to be bimodal when it has this property. Additionally, the angle between two consecutive edges with the same orientation at a given vertex may be labeled as small if it is less than π, or large if it is greater than π. Each source or sink must have exactly one large angle, and each vertex that is neither a source nor a sink must have none. Additionally, each internal face of the drawing must have two more small angles than large ones, and the external face must have two more large angles than small ones. A consistent assignment is a labeling of the angles that satisfies these properties; every upward embedding has a consistent assignment. Conversely, every directed acyclic graph that has a bimodal planar embedding with a consistent assignment has an upward planar drawing, that can be constructed from it in linear time.[3]
Another characterization is possible for graphs with a single source. In this case an upward planar embedding must have the source on the outer face, and every undirected cycle of the graph must have at least one vertex at which both cycle edges are incoming (for instance, the vertex with the highest placement in the drawing). Conversely, if an embedding has both of these properties, then it is equivalent to an upward embedding.[4]
Computational complexity
Several special cases of upward planarity testing are known to be possible in polynomial time:
- Testing whether a graph is st-planar may be accomplished in linear time by adding an edge from s to t and testing whether the remaining graph is planar. Along the same lines, it is possible to construct an upward planar drawing (when it exists) of a directed acyclic graph with a single source and sink, in linear time.[5]
- Testing whether a directed graph with a fixed planar embedding can be drawn upward planar, with an embedding consistent with the given one, can be accomplished by checking that the embedding is bimodal and modeling the consistent assignment problem as a network flow problem. The running time is linear in the size of the input graph, and polynomial in its number of sources and sinks.[6]
- Because oriented polyhedral graphs have a unique planar embedding, the existence of an upward planar drawing for these graphs may be tested in polynomial time.[7]
- Testing whether an outerplanar directed acyclic graph has an upward planar drawing is also polynomial.[8]
- Every series-parallel graph, oriented consistently with the series-parallel structure, is upward planar. An upward planar drawing can be constructed directly from the series-parallel decomposition of the graph.[9] More generally, arbitrary orientations of undirected series-parallel graphs may be tested for upward planarity in polynomial time.[10]
- Every oriented tree is upward planar.[9]
- Every bipartite planar graph, with its edges oriented consistently from one side of the bipartition to the other, is upward planar[9][11]
- A more complicated polynomial time algorithm is known for testing upward planarity of graphs that have a single source, but multiple sinks, or vice versa.[12]
- Testing upward planarity can be performed in polynomial time when there are a constant number of triconnected components and cut vertices, and is fixed-parameter tractable in these two numbers.[13] It is also fixed-parameter tractable in the cyclomatic number of the input graph.[14]
- If the y-coordinates of all vertices are fixed, then a choice of x-coordinates that makes the drawing upward planar can be found in polynomial time.[15]
However, it is NP-complete to determine whether a planar directed acyclic graph with multiple sources and sinks has an upward planar drawing.[16]
Straight-line drawing and area requirements
Fáry's theorem states that every planar graph has a drawing in which its edges are represented by straight line segments, and the same is true of upward planar drawing: every upward planar graph has a straight upward planar drawing.[17] A straight-line upward drawing of a transitively reduced st-planar graph may be obtained by the technique of dominance drawing, with all vertices having integer coordinates within an n × n grid.[18] However, certain other upward planar graphs may require exponential area in all of their straight-line upward planar drawings.[17] If a choice of embedding is fixed, even oriented series parallel graphs and oriented trees may require exponential area.[19]
Hasse diagrams
Upward planar drawings are particularly important for Hasse diagrams of partially ordered sets, as these diagrams are typically required to be drawn upwardly. In graph-theoretic terms, these correspond to the transitively reduced directed acyclic graphs; such a graph can be formed from the covering relation of a partial order, and the partial order itself forms the reachability relation in the graph. If a partially ordered set has one minimal element, has one maximal element, and has an upward planar drawing, then it must necessarily form a lattice, a set in which every pair of elements has a unique greatest lower bound and a unique least upper bound.[20] The Hasse diagram of a lattice is planar if and only if its order dimension is at most two.[21] However, some partial orders of dimension two and with one minimal and maximal element do not have an upward planar drawing (take the order defined by the transitive closure of 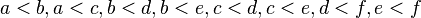 ).
).
References
- Footnotes
- ↑ Garg & Tamassia (1995); Di Battista et al. (1998).
- ↑ Garg & Tamassia (1995), pp. 111–112; Di Battista et al. (1998), 6.1 "Inclusion in a Planar st-Graph", pp. 172–179; Di Battista & Tamassia (1988); Kelly (1987).
- ↑ Garg & Tamassia (1995), pp. 112–115; Di Battista et al. (1998), 6.2 "Angles in Upward Drawings", pp. 180–188; Bertolazzi & Di Battista (1991); Bertolazzi et al. (1994).
- ↑ Garg & Tamassia (1995), p. 115; Di Battista et al. (1998), 6.7.2 "Forbidden Cycles for Single-Source Digraphs", pp. 209–210; Thomassen (1989).
- ↑ Garg & Tamassia (1995), p. 119; Di Battista et al. (1998), p. 179.
- ↑ Garg & Tamassia (1995), pp. 119–121; Di Battista et al. (1998), 6.3 "Upward Planarity Testing of Embedded Digraphs", pp. 188–192; Bertolazzi & Di Battista (1991); Bertolazzi et al. (1994); Abbasi, Healy & Rextin (2010).
- ↑ Di Battista et al. (1998), pp. 191–192; Bertolazzi & Di Battista (1991); Bertolazzi et al. (1994).
- ↑ Garg & Tamassia (1995), pp. 125–126; Di Battista et al. (1998), 6.7.1 "Outerplanar Digraph", p. 209; Papakostas (1995).
- 1 2 3 Di Battista et al. (1998), 6.7.4 "Some Classes of Upward Planar Digraphs", p. 212.
- ↑ Didimo, Giordano & Liotta (2009).
- ↑ Di Battista, Liu & Rival (1990).
- ↑ Garg & Tamassia (1995), pp. 122–125; Di Battista et al. (1998), 6.5 "Optimal Upward Planarity Testing of Single-Source Digraphs", pp. 195–200; Hutton & Lubiw (1996); Bertolazzi et al. (1998).
- ↑ Chan (2004); Healy & Lynch (2006).
- ↑ Healy & Lynch (2006).
- ↑ Jünger & Leipert (1999).
- ↑ Garg & Tamassia (1995), pp. 126–132; Di Battista et al. (1998), 6.6 "Upward Planarity Testing is NP-complete", pp. 201–209; Garg & Tamassia (2001).
- 1 2 Di Battista & Frati (2012); Di Battista, Tamassia & Tollis (1992).
- ↑ Di Battista et al. (1998), 4.7 "Dominance Drawings", pp. 112–127; Di Battista, Tamassia & Tollis (1992).
- ↑ Di Battista & Frati (2012); Bertolazzi et al. (1994); Frati (2008).
- ↑ Di Battista et al. (1998), 6.7.3 "Forbidden Structures for Lattices", pp. 210–212; Platt (1976).
- ↑ Garg & Tamassia (1995), pp. 118; Baker, Fishburn & Roberts (1972).
- Surveys and textbooks
- Di Battista, Giuseppe; Eades, Peter; Tamassia, Roberto; Tollis, Ioannis G. (1998), "Flow and Upward Planarity", Graph Drawing: Algorithms for the Visualization of Graphs, Prentice Hall, pp. 171–213, ISBN 978-0-13-301615-4.
- Di Battista, Giuseppe; Frati, Fabrizio (2012), "Drawing trees, outerplanar graphs, series-parallel graphs, and planar graphs in small area", Thirty Essays on Geometric Graph Theory, Algorithms and combinatorics 29, Springer, pp. 121–165, doi:10.1007/978-1-4614-0110-0_9, ISBN 9781461401100. Section 5, "Upward Drawings", pp. 149–151.
- Garg, Ashim; Tamassia, Roberto (1995), "Upward planarity testing", Order 12 (2): 109–133, doi:10.1007/BF01108622, MR 1354797.
- Research articles
- Abbasi, Sarmad; Healy, Patrick; Rextin, Aimal (2010), "Improving the running time of embedded upward planarity testing", Information Processing Letters 110 (7): 274–278, doi:10.1016/j.ipl.2010.02.004, MR 2642837.
- Baker, K. A.; Fishburn, P. C.; Roberts, F. S. (1972), "Partial orders of dimension 2", Networks 2 (1): 11–28, doi:10.1002/net.3230020103.
- Bertolazzi, Paola; Cohen, Robert F.; Di Battista, Giuseppe; Tamassia, Roberto; Tollis, Ioannis G. (1994), "How to draw a series-parallel digraph", International Journal of Computational Geometry & Applications 4 (4): 385–402, doi:10.1142/S0218195994000215, MR 1310911.
- Bertolazzi, Paola; Di Battista, Giuseppe (1991), "On upward drawing testing of triconnected digraphs", Proceedings of the Seventh Annual Symposium on Computational Geometry (SCG '91, North Conway, New Hampshire, USA), New York, NY, USA: ACM, pp. 272–280, doi:10.1145/109648.109679, ISBN 0-89791-426-0.
- Bertolazzi, P.; Di Battista, G.; Liotta, G.; Mannino, C. (1994), "Upward drawings of triconnected digraphs", Algorithmica 12 (6): 476–497, doi:10.1007/BF01188716, MR 1297810.
- Bertolazzi, Paola; Di Battista, Giuseppe; Mannino, Carlo; Tamassia, Roberto (1998), "Optimal upward planarity testing of single-source digraphs", SIAM Journal on Computing 27 (1): 132–169, doi:10.1137/S0097539794279626, MR 1614821.
- Chan, Hubert (2004), "A parameterized algorithm for upward planarity testing", Proc. 12th European Symposium on Algorithms (ESA '04), Lecture Notes in Computer Science 3221, Springer-Verlag, pp. 157–168, doi:10.1007/978-3-540-30140-0_16.
- Di Battista, Giuseppe; Liu, Wei-Ping; Rival, Ivan (1990), "Bipartite graphs, upward drawings, and planarity", Information Processing Letters 36 (6): 317–322, doi:10.1016/0020-0190(90)90045-Y, MR 1084490.
- Di Battista, Giuseppe; Tamassia, Roberto (1988), "Algorithms for plane representations of acyclic digraphs", Theoretical Computer Science 61 (2-3): 175–198, doi:10.1016/0304-3975(88)90123-5, MR 980241.
- Di Battista, Giuseppe; Tamassia, Roberto; Tollis, Ioannis G. (1992), "Area requirement and symmetry display of planar upward drawings", Discrete and Computational Geometry 7 (4): 381–401, doi:10.1007/BF02187850, MR 1148953.
- Didimo, Walter; Giordano, Francesco; Liotta, Giuseppe (2009), "Upward spirality and upward planarity testing", SIAM Journal on Discrete Mathematics 23 (4): 1842–1899, doi:10.1137/070696854, MR 2594962.
- Frati, Fabrizio (2008), "On minimum area planar upward drawings of directed trees and other families of directed acyclic graphs", International Journal of Computational Geometry & Applications 18 (3): 251–271, doi:10.1142/S021819590800260X, MR 2424444.
- Garg, Ashim; Tamassia, Roberto (2001), "On the computational complexity of upward and rectilinear planarity testing", SIAM Journal on Computing 31 (2): 601–625, doi:10.1137/S0097539794277123, MR 1861292.
- Healy, Patrick; Lynch, Karol (2006), "Two fixed-parameter tractable algorithms for testing upward planarity", International Journal of Foundations of Computer Science 17 (5): 1095–1114, doi:10.1142/S0129054106004285.
- Hutton, Michael D.; Lubiw, Anna (1996), "Upward planar drawing of single-source acyclic digraphs", SIAM Journal on Computing 25 (2): 291–311, doi:10.1137/S0097539792235906, MR 1379303. First presented at the 2nd ACM-SIAM Symposium on Discrete Algorithms, 1991.
- Jünger, Michael; Leipert, Sebastian (1999), "Level planar embedding in linear time", Graph Drawing (Proc. GD '99), Lecture Notes in Computer Science 1731, pp. 72–81, doi:10.1007/3-540-46648-7_7, ISBN 978-3-540-66904-3.
- Kelly, David (1987), "Fundamentals of planar ordered sets", Discrete Mathematics 63 (2-3): 197–216, doi:10.1016/0012-365X(87)90008-2, MR 885497.
- Papakostas, Achilleas (1995), "Upward planarity testing of outerplanar dags (extended abstract)", Graph Drawing: DIMACS International Workshop, GD '94, Princeton, New Jersey, USA, October 10–12, 1994, Proceedings, Lecture Notes in Computer Science 894, Berlin: Springer, pp. 298–306, doi:10.1007/3-540-58950-3_385, MR 1337518.
- Platt, C. R. (1976), "Planar lattices and planar graphs", Journal of Combinatorial Theory, Ser. B 21 (1): 30––39, doi:10.1016/0095-8956(76)90024-1.
- Thomassen, Carsten (1989), "Planar acyclic oriented graphs", Order 5 (4): 349–361, doi:10.1007/BF00353654, MR 1010384.