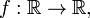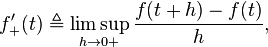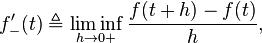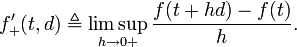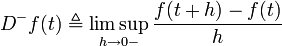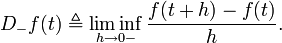Dini derivative
In mathematics and, specifically, real analysis, the Dini derivatives (or Dini derivates) are a class of generalizations of the derivative. They were introduced by Ulisse Dini.
The upper Dini derivative, which is also called an upper right-hand derivative,[1] of a continuous function
is denoted by 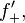 and defined by
and defined by
where 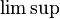 is the supremum limit and the limit is a one-sided limit. The lower Dini derivative,
is the supremum limit and the limit is a one-sided limit. The lower Dini derivative, 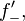 , is defined by
, is defined by
where 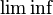 is the infimum limit.
is the infimum limit.
If  is defined on a vector space, then the upper Dini derivative at
is defined on a vector space, then the upper Dini derivative at  in the direction
in the direction 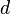 is defined by
is defined by
If  is locally Lipschitz, then
is locally Lipschitz, then 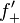 is finite. If
is finite. If  is differentiable at
is differentiable at  , then the Dini derivative at
, then the Dini derivative at  is the usual derivative at
is the usual derivative at  .
.
Remarks
- Sometimes the notation
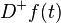 is used instead of
is used instead of 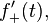 and
and 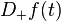 is used instead of
is used instead of 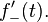 [1]
[1]
- Also,
and
- So when using the
 notation of the Dini derivatives, the plus or minus sign indicates the left- or right-hand limit, and the placement of the sign indicates the infimum or supremum limit.
notation of the Dini derivatives, the plus or minus sign indicates the left- or right-hand limit, and the placement of the sign indicates the infimum or supremum limit.
- On the extended reals, each of the Dini derivatives always exist; however, they may take on the values
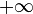 or
or 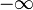 at times (i.e., the Dini derivatives always exist in the extended sense).
at times (i.e., the Dini derivatives always exist in the extended sense).
See also
References
- In-line references
- 1 2 Khalil, H.K. (2002). Nonlinear Systems (3rd ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-067389-7.
- General references
- Lukashenko, T.P. (2001), "Dini derivative", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4.
- Royden, H.L. (1968). Real analysis (2nd ed.). MacMillan. ISBN 978-0-02-404150-0.
- Brian S. Thomson; Judith B. Bruckner; Andrew M. Bruckner (2008). Elementary Real Analysis. ClassicalRealAnalysis.com [first edition published by Prentice Hall in 2001]. pp. 301–302. ISBN 978-1-4348-4161-2.
This article incorporates material from Dini derivative on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.