List of unsolved problems in mathematics
Since the Renaissance, every century has seen the solution of more mathematical problems than the century before, and yet many mathematical problems, both major and minor, still elude solution.[1] Most graduate students, in order to earn a Ph.D. in mathematics, are expected to produce new, original mathematics. That is, they are expected to solve problems that are not routine, and which cannot be solved by standard methods.
In the context of this article, a mathematical problem is a statement (conjecture) that no one knows whether it is true or not. The problem is to determine whether it is true or false. The task of the problem solver is to either produce a proof of the statement or a proof that the statement is false.
An unsolved problem in mathematics does not refer to the kind of problem found as an exercise in a textbook, but rather to the answer to a major question or a general method that provides a solution to an entire class of problems. Prizes are often awarded for the solution to a long-standing problem, and lists of unsolved problems receive considerable attention. This article reiterates the list of Millennium Prize Problems of unsolved problems in mathematics (includes problems of physics and computer science) as of August 2015, and lists further unsolved problems in algebra, additive and algebraic number theories, analysis, combinatorics, algebraic, discrete, and Euclidean geometries, dynamical systems, partial differential equations, and graph, group, model, number, set and Ramsey theories, as well as miscellaneous unsolved problems. A list of problems solved since 1975 also appears, alongside some sources, general and specific, for the stated problems.
Lists of unsolved problems in mathematics
Over the course of time, several lists of unsolved mathematical problems have appeared. The following is a listing of those lists.
| List | Number of problems | Proposed by | Proposed in |
|---|---|---|---|
| Hilbert's problems | 23 | David Hilbert | 1900 |
| Landau's problems | 4 | Edmund Landau | 1912 |
| Taniyama's problems[2] | 36 | Yutaka Taniyama | 1955 |
| Thurston's 24 questions[3][4] | 24 | William Thurston | 1982 |
| Smale's problems | 18 | Stephen Smale | 1998 |
| Millennium Prize problems | 7 | Clay Mathematics Institute | 2000 |
| Unsolved Problems on Mathematics for the 21st Century[5] | 22 | Jair Minoro Abe, Shotaro Tanaka | 2001 |
| DARPA's math challenges[6][7] | 23 | DARPA | 2007 |
Millennium Prize Problems
Of the original seven Millennium Prize Problems set by the Clay Mathematics Institute, six have yet to be solved, as of August 2015:[8]
- P versus NP
- Hodge conjecture
- Riemann hypothesis
- Yang–Mills existence and mass gap
- Navier–Stokes existence and smoothness
- Birch and Swinnerton-Dyer conjecture
The seventh problem, the Poincaré conjecture, has been solved.[9] The smooth four-dimensional Poincaré conjecture—that is, whether a four-dimensional topological sphere can have two or more inequivalent smooth structures—is still unsolved.[10]
Other still-unsolved problems
Additive number theory
- Beal's conjecture
- Fermat–Catalan conjecture
- Goldbach's conjecture
- The values of g(k) and G(k) in Waring's problem
- Collatz conjecture (3n + 1 conjecture)
- Lander, Parkin, and Selfridge conjecture
- Diophantine quintuples
- Gilbreath's conjecture
- Erdős conjecture on arithmetic progressions
- Erdős–Turán conjecture on additive bases
- Pollock octahedral numbers conjecture
- Skolem problem
Algebra
- Hilbert's sixteenth problem
- Hadamard conjecture
- Jacobson's conjecture
- Existence of perfect cuboids and associated Cuboid conjectures
- Zauner's conjecture: existence of SIC-POVMs in all dimensions
- Wild Problem: Classification of pairs of n×n matrices under simultaneous conjugation and problems containing it such as a lot of classification problems
Algebraic geometry
- André–Oort conjecture
- Bass conjecture
- Deligne conjecture
- Fröberg conjecture
- Fujita conjecture
- Hartshorne conjectures
- Jacobian conjecture
- Manin conjecture
- Nakai conjecture
- Resolution of singularities in characteristic p
- Standard conjectures on algebraic cycles
- Section conjecture
- Tate conjecture
- Virasoro conjecture
- Witten conjecture
- Zariski multiplicity conjecture
Algebraic number theory
- Are there infinitely many real quadratic number fields with unique factorization?
- Brumer–Stark conjecture
- Characterize all algebraic number fields that have some power basis.
Analysis
- The Jacobian conjecture
- Schanuel's conjecture
- Lehmer's conjecture
- Pompeiu problem
- Are
 (the Euler–Mascheroni constant), π + e, π − e, πe, π/e, πe, π√2, ππ, eπ2, ln π, 2e, ee, Catalan's constant or Khinchin's constant rational, algebraic irrational, or transcendental? What is the irrationality measure of each of these numbers?[11][12][13]
(the Euler–Mascheroni constant), π + e, π − e, πe, π/e, πe, π√2, ππ, eπ2, ln π, 2e, ee, Catalan's constant or Khinchin's constant rational, algebraic irrational, or transcendental? What is the irrationality measure of each of these numbers?[11][12][13] - The Khabibullin’s conjecture on integral inequalities
Combinatorics
- Number of magic squares (sequence A006052 in OEIS)
- Finding a formula for the probability that two elements chosen at random generate the symmetric group

- Frankl's union-closed sets conjecture: for any family of sets closed under sums there exists an element (of the underlying space) belonging to half or more of the sets
- The Lonely runner conjecture: if
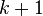 runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be at least a distance
runners with pairwise distinct speeds run round a track of unit length, will every runner be "lonely" (that is, be at least a distance 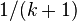 from each other runner) at some time?
from each other runner) at some time? - Singmaster's conjecture: is there a finite upper bound on the multiplicities of the entries greater than 1 in Pascal's triangle?
- The 1/3–2/3 conjecture: does every finite partially ordered set that is not totally ordered contain two elements x and y such that the probability that x appears before y in a random linear extension is between 1/3 and 2/3?
Discrete geometry
- Solving the happy ending problem for arbitrary

- Finding matching upper and lower bounds for K-sets and halving lines
- The Hadwiger conjecture on covering n-dimensional convex bodies with at most 2n smaller copies
- The Kobon triangle problem on triangles in line arrangements
- The McMullen problem on projectively transforming sets of points into convex position
- Ulam's packing conjecture about the identity of the worst-packing convex solid
Euclidean geometry
- The einstein problem – does there exist a two-dimensional shape that forms the prototile for an aperiodic tiling, but not for any periodic tiling?[14]
- Inscribed square problem – does every Jordan curve have an inscribed square?[15]
- Moser's worm problem – what is the smallest area of a shape that can cover every unit-length curve in the plane?[16]
- The moving sofa problem – what is the largest area of a shape that can be maneuvered through a unit-width L-shaped corridor?[17]
- Shephard's problem (a.k.a. Dürer's conjecture) – does every convex polyhedron have a net?[18]
- The Thomson problem - what is the minimum energy configuration of N particles bound to the surface of a unit sphere that repel each other with a 1/r potential (or any potential in general)?
- Pentagonal tiling - 15 types of convex pentagons are known to monohedrally tile the plane, and it is not known whether this list is complete.[19]
Dynamical systems
- Furstenberg conjecture – Is every invariant and ergodic measure for the
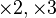 action on the circle either Lebesgue or atomic?
action on the circle either Lebesgue or atomic? - Margulis conjecture — Measure classification for diagonalizable actions in higher-rank groups
- MLC conjecture – Is the Mandelbrot set locally connected ?
- Weinstein conjecture - Does a regular compact contact type level set of a Hamiltonian on a symplectic manifold carry at least one periodic orbit of the Hamiltonian flow?
- Is every reversible cellular automaton in three or more dimensions locally reversible?[20]
Graph theory
- Barnette's conjecture that every cubic bipartite three-connected planar graph has a Hamiltonian cycle
- The Erdős–Gyárfás conjecture on cycles with power-of-two lengths in cubic graphs
- The Erdős–Hajnal conjecture on finding large homogeneous sets in graphs with a forbidden induced subgraph
- The Hadwiger conjecture relating coloring to clique minors
- The Erdős–Faber–Lovász conjecture on coloring unions of cliques
- Harborth's conjecture that every planar graph can be drawn with integer edge lengths
- The total coloring conjecture
- The list coloring conjecture
- The Ringel–Kotzig conjecture on graceful labeling of trees
- The Hadwiger–Nelson problem on the chromatic number of unit distance graphs
- Deriving a closed-form expression for the percolation threshold values, especially
 (square site)
(square site) - Tutte's conjectures that every bridgeless graph has a nowhere-zero 5-flow and every bridgeless graph without the Petersen graph as a minor has a nowhere-zero 4-flow
- The reconstruction conjecture and new digraph reconstruction conjecture concerning whether or not a graph is recognizable by the vertex deleted subgraphs.
- The cycle double cover conjecture that every bridgeless graph has a family of cycles that includes each edge twice.
- Does a Moore graph with girth 5 and degree 57 exist?
- Conway's thrackle conjecture
- Negami's conjecture on the characterization of graphs with planar covers
- The Blankenship–Oporowski conjecture on the book thickness of subdivisions
Group theory
- Is every finitely presented periodic group finite?
- The inverse Galois problem: is every finite group the Galois group of a Galois extension of the rationals?
- For which positive integers m, n is the free Burnside group B(m,n) finite? In particular, is B(2, 5) finite?
- Is every group surjunctive?
Model theory
- Vaught's conjecture
- The Cherlin–Zilber conjecture: A simple group whose first-order theory is stable in
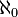 is a simple algebraic group over an algebraically closed field.
is a simple algebraic group over an algebraically closed field. - The Main Gap conjecture, e.g. for uncountable first order theories, for AECs, and for
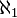 -saturated models of a countable theory.[21]
-saturated models of a countable theory.[21] - Determine the structure of Keisler's order[22][23]
- The stable field conjecture: every infinite field with a stable first-order theory is separably closed.
- Is the theory of the field of Laurent series over
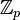 decidable? of the field of polynomials over
decidable? of the field of polynomials over 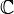 ?
? - (BMTO) Is the Borel monadic theory of the real order decidable? (MTWO) Is the monadic theory of well-ordering consistently decidable?[24]
- The Stable Forking Conjecture for simple theories[25]
- For which number fields does Hilbert's tenth problem hold?
- Assume K is the class of models of a countable first order theory omitting countably many types. If K has a model of cardinality
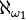 does it have a model of cardinality continuum?[26]
does it have a model of cardinality continuum?[26] - Is there a logic L which satisfies both the Beth property and Δ-interpolation, is compact but does not satisfy the interpolation property?[27]
- If the class of atomic models of a complete first order theory is categorical in the
 , is it categorical in every cardinal?[28][29]
, is it categorical in every cardinal?[28][29] - Is every infinite, minimal field of characteristic zero algebraically closed? (minimal = no proper elementary substructure)
- Kueker's conjecture[30]
- Does there exist an o-minimal first order theory with a trans-exponential (rapid growth) function?
- Lachlan's decision problem
- Does a finitely presented homogeneous structure for a finite relational language have finitely many reducts?
- Do the Henson graphs have the finite model property? (e.g. triangle-free graphs)
- The universality problem for C-free graphs: For which finite sets C of graphs does the class of C-free countable graphs have a universal member under strong embeddings?[31]
- The universality spectrum problem: Is there a first-order theory whose universality spectrum is minimum?[32]
Number theory (general)
- abc conjecture (Proof claimed in 2012, currently under review.)
- Carmichael's totient function conjecture
- Erdős–Straus conjecture
- Do any odd perfect numbers exist?
- Are there infinitely many perfect numbers?
- Do quasiperfect numbers exist?
- Do any odd weird numbers exist?
- Do any Lychrel numbers exist?
- Is 10 a solitary number?
- Do any Taxicab(5, 2, n) exist for n>1?
- Brocard's problem: existence of integers, (n,m), such that n!+1 = m2 other than n=4, 5, 7
- Littlewood conjecture
- Congruent number problem (a corollary to Birch and Swinnerton-Dyer conjecture, per Tunnell's theorem)
- Lehmer's totient problem: if φ(n) divides n − 1, must n be prime?
- Are there infinitely many amicable numbers?
- Are there any pairs of amicable numbers which have opposite parity?
- Are there any pairs of relatively prime amicable numbers?
- Are there infinitely many betrothed numbers?
- Are there any pairs of betrothed numbers which have same parity?
- The Gauss circle problem – how far can the number of integer points in a circle centered at the origin be from the area of the circle?
Number theory (prime numbers)
- Catalan's Mersenne conjecture
- Goldbach's conjecture
- Twin prime conjecture
- Legendre's conjecture
- Polignac's conjecture
- Dickson's conjecture
- Bunyakovsky conjecture
- The Gaussian moat problem: is it possible to find an infinite sequence of distinct Gaussian prime numbers such that the difference between consecutive numbers in the sequence is bounded?
- Are there infinitely many prime quadruplets?
- Are there infinitely many cousin primes?
- Are there infinitely many sexy primes?
- Are there infinitely many Mersenne primes (Lenstra–Pomerance–Wagstaff conjecture); equivalently, infinitely many even perfect numbers?
- Are there infinitely many Wagstaff primes?
- Are there infinitely many Sophie Germain primes?
- Are there infinitely many Pierpont primes?
- Are there infinitely many regular primes, and if so is their relative density
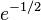 ?
? - Are there infinitely many repunit primes to every base except perfect power and numbers of the form -4k4?
- Are there infinitely many Cullen primes?
- Are there infinitely many Woodall primes?
- Are there infinitely many palindromic primes to every base?
- Are there infinitely many Fibonacci primes?
- Are there infinitely many Lucas primes?
- Are there infinitely many Pell primes?
- Are there infinitely many Newman–Shanks–Williams primes?
- Are all Mersenne numbers of prime index square-free?
- Are there infinitely many Wieferich primes?
- Are there any Wieferich prime in base 47?
- Are there any composite c satisfying 2c - 1 ≡ 1 (mod c2)?
- For any given integer a > 0, are there infinitely many primes p such that ap - 1 ≡ 1 (mod p2)?[33]
- Can a prime p satisfy 2p − 1 ≡ 1 (mod p2) and 3p − 1 ≡ 1 (mod p2) simultaneously?[34]
- Are there infinitely many Wilson primes?
- Are there infinitely many Wolstenholme primes?
- Are there any Wall–Sun–Sun primes?
- Is every Fermat number 22n + 1 composite for
 ?
? - Are all Fermat numbers square-free?
- For any given integer a which is not a square and does not equal to -1. Are there infinitely many primes with a as a primitive root?
- Artin's conjecture on primitive roots
- Is 78,557 the lowest Sierpiński number?
- Is 509,203 the lowest Riesel number?
- Fortune's conjecture (that no Fortunate number is composite)
- Landau's problems
- Does every prime number appear in the Euclid–Mullin sequence?
- Does the converse of Wolstenholme's theorem hold for all natural numbers?
- Elliott–Halberstam conjecture
Partial differential equations
- Regularity of solutions of Vlasov–Maxwell equations
- Regularity of solutions of Euler equations
Ramsey theory
- The values of the Ramsey numbers, particularly
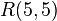
- The values of the Van der Waerden numbers
Set theory
- The problem of finding the ultimate core model, one that contains all large cardinals.
- If ℵω is a strong limit cardinal, then 2ℵω < ℵω1 (see Singular cardinals hypothesis). The best bound, ℵω4, was obtained by Shelah using his pcf theory.
- Woodin's Ω-hypothesis.
- Does the consistency of the existence of a strongly compact cardinal imply the consistent existence of a supercompact cardinal?
- (Woodin) Does the Generalized Continuum Hypothesis below a strongly compact cardinal imply the Generalized Continuum Hypothesis everywhere?
- Does there exist a Jónsson algebra on ℵω?
- Without assuming the axiom of choice, can a nontrivial elementary embedding V→V exist?
- Does the Generalized Continuum Hypothesis entail
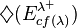 for every singular cardinal
for every singular cardinal  ?
?
Other
- Invariant subspace problem
- Problems in Latin squares
- Problems in loop theory and quasigroup theory
- Dixmier conjecture
- Baum–Connes conjecture
- Novikov conjecture
- Generalized star height problem
- Assorted sphere packing problems, e.g. the densest irregular hypersphere packings
- Closed curve problem: Find (explicit) necessary and sufficient conditions that determine when, given two periodic functions with the same period, the integral curve is closed.[35]
- Toeplitz' conjecture (open since 1911)
Problems solved since 1975
- Goldbach's weak conjecture (Harald Helfgott, 2013)[36][37][38]
- Kadison–Singer problem (Adam Marcus, Daniel Spielman and Nikhil Srivastava, 2013)[39][40]
- Willmore conjecture (Fernando Codá Marques and André Neves, 2012)[41]
- Gromov's problem on distortion of knots (John Pardon, 2011)[42]
- Circular law (Terence Tao and Van H. Vu, 2010)[43]
- Hirsch conjecture (Francisco Santos Leal, 2010)[44][45]
- Serre's modularity conjecture (Chandrashekhar Khare and Jean-Pierre Wintenberger, 2008)[46][47][48]
- Heterogeneous tiling conjecture (squaring the plane) (Frederick V. Henle and James M. Henle, 2007)
- Weinstein conjecture for closed 3-dimensional manifolds (Clifford Taubes, 2007)[49]
- Road coloring conjecture (Avraham Trahtman, 2007)[50]
- The Angel problem (Various independent proofs, 2006)
- The Langlands–Shelstad fundamental lemma (Ngô Bảo Châu and Gérard Laumon, 2004)[51]
- Stanley–Wilf conjecture (Gábor Tardos and Adam Marcus, 2004)[52]
- Green–Tao theorem (Ben J. Green and Terence Tao, 2004)[53]
- Cameron–Erdős conjecture (Ben J. Green, 2003, Alexander Sapozhenko, 2003)[54][55]
- Strong perfect graph conjecture (Maria Chudnovsky, Neil Robertson, Paul Seymour and Robin Thomas, 2002)
- Poincaré conjecture (Grigori Perelman, 2002)[56]
- Catalan's conjecture (Preda Mihăilescu, 2002)[57]
- Kato's conjecture (Auscher, Hofmann, Lacey, McIntosh, and Tchamitchian, 2001)
- The Langlands correspondence for function fields (Laurent Lafforgue, 1999)[58]
- Taniyama–Shimura conjecture (Wiles, Breuil, Conrad, Diamond, and Taylor, 1999)
- Kepler conjecture (Thomas Hales, 1998)
- Milnor conjecture (Vladimir Voevodsky, 1996)
- Fermat's Last Theorem (Andrew Wiles and Richard Taylor, 1995)
- Bieberbach conjecture (Louis de Branges, 1985)[59]
- Princess and monster game (Shmuel Gal, 1979) [60][61][62]
- Four-color theorem (Appel and Haken, 1977)
References
- ↑ Eves, An Introduction to the History of Mathematics 6th Edition, Thomson, 1990, ISBN 978-0-03-029558-4.
- ↑ Shimura, G. (1989). "Yutaka Taniyama and his time". Bulletin of the London Mathematical Society 21 (2): 186–196. doi:10.1112/blms/21.2.186.
- ↑ http://www.uni-regensburg.de/Fakultaeten/nat_Fak_I/friedl/papers/dmv_091514.pdf
- ↑ http://www.ams.org/journals/bull/1982-06-03/S0273-0979-1982-15003-0/S0273-0979-1982-15003-0.pdf THREE DIMENSIONAL MANIFOLDS, KLEINIAN GROUPS AND HYPERBOLIC GEOMETRY
- ↑ Abe, Jair Minoro; Tanaka, Shotaro (2001). Unsolved Problems on Mathematics for the 21st Century. IOS Press. ISBN 9051994907.
- ↑ "DARPA invests in math". CNN. 2008-10-14. Archived from the original on 2009-03-04. Retrieved 2013-01-14.
- ↑ "Broad Agency Announcement (BAA 07-68) for Defense Sciences Office (DSO)". DARPA. 2007-09-10. Archived from the original on 2012-10-01. Retrieved 2013-06-25.
- ↑ http://claymath.org/millennium-problems
- ↑ "Poincaré Conjecture". Clay Mathematics Institute.
- ↑ http://www.openproblemgarden.org/?q=op/smooth_4_dimensional_poincare_conjecture
- ↑ For background on the numbers that are the focus of this problem, see articles by Eric W. Weisstein, on pi (), e (), Khinchin's Constant (), irrational numbers (), transcendental numbers (), and irrationality measures () at Wolfram MathWorld, all articles accessed 15 December 2014.
- ↑ Michel Waldschmidt, 2008, "An introduction to irrationality and transcendence methods," at The University of Arizona The Southwest Center for Arithmetic Geometry 2008 Arizona Winter School, March 15–19, 2008 (Special Functions and Transcendence), see , accessed 15 December 2014.
- ↑ John Albert, posting date unknown, "Some unsolved problems in number theory" [from Victor Klee & Stan Wagon, "Old and New Unsolved Problems in Plane Geometry and Number Theory"], in University of Oklahoma Math 4513 course materials, see , accessed 15 December 2014.
- ↑ Socolar, Joshua E. S.; Taylor, Joan M. (2012), "Forcing nonperiodicity with a single tile", The Mathematical Intelligencer 34 (1): 18–28, arXiv:1009.1419, doi:10.1007/s00283-011-9255-y, MR 2902144.
- ↑ Matschke, Benjamin (2014), "A survey on the square peg problem", Notices of the American Mathematical Society 61 (4): 346–253, doi:10.1090/noti1100.
- ↑ Norwood, Rick; Poole, George; Laidacker, Michael (1992), "The worm problem of Leo Moser", Discrete and Computational Geometry 7 (2): 153–162, doi:10.1007/BF02187832, MR 1139077.
- ↑ Wagner, Neal R. (1976), "The Sofa Problem" (PDF), The American Mathematical Monthly 83 (3): 188–189, doi:10.2307/2977022, JSTOR 2977022
- ↑ Demaine, Erik D.; O'Rourke, Joseph (2007), "Chapter 22. Edge Unfolding of Polyhedra", Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge University Press, pp. 306–338.
- ↑ Bellos, Alex (11 August 2015), "Attack on the pentagon results in discovery of new mathematical tile", The Guardian
- ↑ Kari, Jarkko (2009), "Structure of reversible cellular automata", Unconventional Computation: 8th International Conference, UC 2009, Ponta Delgada, Portugal, September 7ÔÇô11, 2009, Proceedings, Lecture Notes in Computer Science 5715, Springer, p. 6, doi:10.1007/978-3-642-03745-0_5.
- ↑ Shelah S, Classification Theory, North-Holland, 1990
- ↑ Keisler, HJ, "Ultraproducts which are not saturated." J. Symb Logic 32 (1967) 23—46.
- ↑ Malliaris M, Shelah S, "A dividing line in simple unstable theories." http://arxiv.org/abs/1208.2140
- ↑ Gurevich, Yuri, "Monadic Second-Order Theories," in J. Barwise, S. Feferman, eds., Model-Theoretic Logics (New York: Springer-Verlag, 1985), 479–506.
- ↑ Peretz, Assaf, "Geometry of forking in simple theories." J. Symbolic Logic Volume 71, Issue 1 (2006), 347–359.
- ↑ Shelah, Saharon (1999). "Borel sets with large squares". Fundamenta Mathematicae 159 (1): 1–50. arXiv:math/9802134.
- ↑ Makowsky J, "Compactness, embeddings and definability," in Model-Theoretic Logics, eds Barwise and Feferman, Springer 1985 pps. 645–715.
- ↑ Baldwin, John T. (July 24, 2009). Categoricity (PDF). American Mathematical Society. ISBN 978-0821848937. Retrieved February 20, 2014.
- ↑ Shelah, Saharon. "Introduction to classification theory for abstract elementary classes".
- ↑ Hrushovski, Ehud, "Kueker's conjecture for stable theories." Journal of Symbolic Logic Vol. 54, No. 1 (Mar., 1989), pp. 207–220.
- ↑ Cherlin, G.; Shelah, S. (May 2007). "Universal graphs with a forbidden subtree". Journal of Combinatorial Theory, Series B 97 (3): 293–333. arXiv:math/0512218. doi:10.1016/j.jctb.2006.05.008.
- ↑ Džamonja, Mirna, "Club guessing and the universal models." On PCF, ed. M. Foreman, (Banff, Alberta, 2004).
- ↑ Ribenboim, P. (2006). Die Welt der Primzahlen (in German) (2nd ed.). Springer. pp. 242–243. doi:10.1007/978-3-642-18079-8. ISBN 978-3-642-18078-1.
- ↑ Dobson, J. B. (June 2012) [2011], On Lerch's formula for the Fermat quotient, p. 15, arXiv:1103.3907
- ↑ Barros, Manuel (1997), "General Helices and a Theorem of Lancret", American Mathematical Society 125: 1503–1509, JSTOR 2162098.
- ↑ Helfgott, Harald A. (2013). "Major arcs for Goldbach's theorem". arXiv:1305.2897 [math.NT].
- ↑ Helfgott, Harald A. (2012). "Minor arcs for Goldbach's problem". arXiv:1205.5252 [math.NT].
- ↑ Helfgott, Harald A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748 [math.NT].
- ↑ Casazza, Peter G.; Fickus, Matthew; Tremain, Janet C.; Weber, Eric (2006). Han, Deguang; Jorgensen, Palle E. T.; Larson, David Royal, eds. "The Kadison-Singer problem in mathematics and engineering: A detailed account". Contemporary Mathematics. Large Deviations for Additive Functionals of Markov Chains: The 25th Great Plains Operator Theory Symposium, June 7–12, 2005, University of Central Florida, Florida (American Mathematical Society.) 414: 299–355. doi:10.1090/conm/414/07820. ISBN 978-0-8218-3923-2. Retrieved 24 April 2015.
- ↑ Mackenzie, Dana. "Kadison–Singer Problem Solved" (PDF). SIAM News (January/February 2014) (Society for Industrial and Applied Mathematics). Retrieved 24 April 2015.
- ↑ Marques, Fernando C.; Neves, André (2013). "Min-max theory and the Willmore conjecture". Annals of Mathematics. arXiv:1202.6036. doi:10.4007/annals.2014.179.2.6.
- ↑ "2012 Morgan Prize" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 59 (4): 569–571. ISSN 1088-9477. OCLC 34550461.
- ↑ Tao, Terence; Vu, Van (2010). appendix by Manjunath Krishnapur. "Random matrices: Universality of ESD and the Circular Law". Annals of Probability 38 (5): 2023–2065. arXiv:0807.4898. doi:10.1214/10-AOP534. MR 2722794.
- ↑ Santos, Franciscos (2012). "A counterexample to the Hirsch conjecture". Annals of Mathematics (Princeton University and Institute for Advanced Study) 176 (1): 383–412. doi:10.4007/annals.2012.176.1.7.
- ↑ Ziegler, Günter M. (2012). "Who solved the Hirsch conjecture?". Documenta Mathematica. Extra Volume "Optimization Stories": 75–85.
- ↑ Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), "Serre’s modularity conjecture (I)", Inventiones Mathematicae 178 (3): 485–504, doi:10.1007/s00222-009-0205-7
- ↑ Khare, Chandrashekhar; Wintenberger, Jean-Pierre (2009), "Serre’s modularity conjecture (II)", Inventiones Mathematicae 178 (3): 505–586, doi:10.1007/s00222-009-0206-6
- ↑ "2011 Cole Prize in Number Theory" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 58 (4): 610–611. ISSN 1088-9477. OCLC 34550461.
- ↑ Jackson, Allyn (May 2008). "Taubes Receives NAS Award in Mathematics" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 55 (5): 596–597. ISSN 1088-9477. OCLC 34550461.
- ↑ Seigel-Itzkovich, Judy (2008-02-08). "Russian immigrant solves math puzzle". The Jerusalem Post. Retrieved 2015-11-12.
- ↑ "Fields Medal – Ngô Bảo Châu". International Congress of Mathematicians 2010. ICM. 19 August 2010. Retrieved 2015-11-12.
Ngô Bảo Châu is being awarded the 2010 Fields Medal for his proof of the Fundamental Lemma in the theory of automorphic forms through the introduction of new algebro-geometric methods.
- ↑ Chung, Fan; Greene, Curtis; Hutchinson, Joan (April 2015). "Herbert S. Wilf (1931–2012)" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 62 (4): 358. ISSN 1088-9477. OCLC 34550461.
The conjecture was finally given an exceptionally elegant proof by A. Marcus and G. Tardos in 2004.
- ↑ "Bombieri and Tao Receive King Faisal Prize" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 57 (5): 642–643. May 2010. ISSN 1088-9477. OCLC 34550461.
Working with Ben Green, he proved there are arbitrarily long arithmetic progressions of prime numbers—a result now known as the Green–Tao theorem.
- ↑ Green, Ben (2004), "The Cameron–Erdős conjecture", The Bulletin of the London Mathematical Society 36 (6): 769–778, arXiv:math.NT/0304058, doi:10.1112/S0024609304003650, MR 2083752
- ↑ "News from 2007". American Mathematical Society. AMS. 31 December 2007. Retrieved 2015-11-13.
The 2007 prize also recognizes Green for "his many outstanding results including his resolution of the Cameron-Erdős conjecture..."
- ↑ "Prize for Resolution of the Poincaré Conjecture Awarded to Dr. Grigoriy Perelman" (PDF) (Press release). Clay Mathematics Institute. March 18, 2010. Retrieved November 13, 2015.
The Clay Mathematics Institute hereby awards the Millennium Prize for resolution of the Poincaré conjecture to Grigoriy Perelman.
- ↑ Metsänkylä, Tauno (5 September 2003). "Catalan's conjecture: another old diophantine problem solved" (PDF). Bulletin of the American Mathematical Society (American Mathematical Society) 41 (1): 43–57. ISSN 0273-0979.
The conjecture, which dates back to 1844, was recently proven by the Swiss mathematician Preda Mihăilescu.
- ↑ Friedlander, Eric; Rapoport, Michael; Suslin, Andrei (February 2003). "The Mathematical Work of the 2002 Fields Medalists" (PDF). Notices of the AMS (Providence, Rhode Island, United States: American Mathematical Society) 50 (2): 212–217. ISSN 1088-9477. OCLC 34550461.
Laurent Lafforgue was awarded the Fields Medal for his proof of the Langlands correspondence for the general linear groups GLr over function fields of positive characteristic.
- ↑ Korevaar, Jacob (September 1986). "Ludwig Bieberbach's conjecture and its proof by Louis de Branges" (PDF). The American Mathematical Monthly (Mathematical Association of America) 93: 505–514. ISSN 0002-9890.
- ↑ S. Gal, SEARCH GAMES, Academic Press, New York (1980).
- ↑ Gal Shmuel (1979). "Search games with mobile and immobile hider". SIAM J. Control Optim. 17 (1): 99–122. doi:10.1137/0317009. MR 0516859.
- ↑ A. Garnaev (1992). "A Remark on the Princess and Monster Search Game" (PDF). Int. J. Game Theory 20 (3): 269–276. doi:10.1007/BF01253781.
Further reading
Books discussing unsolved problems
- Fan Chung; Graham, Ron (1999). Erdos on Graphs: His Legacy of Unsolved Problems. AK Peters. ISBN 1-56881-111-X.
- Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1994). Unsolved Problems in Geometry. Springer. ISBN 0-387-97506-3.
- Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer. ISBN 0-387-20860-7.
- Klee, Victor; Wagon, Stan (1996). Old and New Unsolved Problems in Plane Geometry and Number Theory. The Mathematical Association of America. ISBN 0-88385-315-9.
- Du Sautoy, Marcus (2003). The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics. Harper Collins. ISBN 0-06-093558-8.
- Derbyshire, John (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. Joseph Henry Press. ISBN 0-309-08549-7.
- Devlin, Keith (2006). The Millennium Problems – The Seven Greatest Unsolved* Mathematical Puzzles Of Our Time. Barnes & Noble. ISBN 978-0-7607-8659-8.
- Blondel, Vincent D.; Megrestski, Alexandre (2004). Unsolved problems in mathematical systems and control theory. Princeton University Press. ISBN 0-691-11748-9.
- Lizhen Ji, [various]; Yat-Sun Poon, Shing-Tung Yau (2013). Open Problems and Surveys of Contemporary Mathematics (volume 6 in the Surveys in Modern Mathematics series) (Surveys of Modern Mathematics). International Press of Boston. ISBN 1-571-46278-3.
Books discussing recently solved problems
- Singh, Simon (2002). Fermat's Last Theorem. Fourth Estate. ISBN 1-84115-791-0.
- O'Shea, Donal (2007). The Poincaré Conjecture. Penguin. ISBN 978-1-84614-012-9.
- Szpiro, George G. (2003). Kepler's Conjecture. Wiley. ISBN 0-471-08601-0.
- Ronan, Mark (2006). Symmetry and the Monster. Oxford. ISBN 0-19-280722-6.
Other works
- Waldschmidt, Michel (2004). "Open Diophantine Problems" (PDF). Moscow Mathematical Journal 4 (1): 245–305. ISSN 1609-3321. Zbl 1066.11030.
- Mazurov, V. D.; Khukhro, E. I. (1 Jun 2015). "Unsolved Problems in Group Theory. The Kourovka Notebook. No. 18 (English version)". arXiv:1401.0300v6.
- Thomas, Robin (1998), "An Update on the Four-Color Theorem" (http://www.ams.org/notices/199807/thomas.pdf) (PDF), Notices of the American Mathematical Society 45 (7), pp. 848–859, MR 1633714
External links
- Ball, John M. "Some Open Problems in Elasticity" (PDF).
- Constantin, Peter. "Some open problems and research directions in the mathematical study of fluid dynamics" (PDF).
- Serre, Denis. "Five Open Problems in Compressible Mathematical Fluid Dynamics" (PDF).
- Unsolved Problems in Number Theory, Logic and Cryptography
- Clay Institute Millennium Prize
- List of links to unsolved problems in mathematics, prizes and research.
- Open Problem Garden The collection of open problems in mathematics build on the principle of user editable ("wiki") site
- AIM Problem Lists
- Unsolved Problem of the Week Archive. MathPro Press.
- The Open Problems Project (TOPP), discrete and computational geometry problems
- Kirby's list of unsolved problems in low-dimensional topology
- Erdös' Problems on Graphs
| ||||||