Universality class

In statistical mechanics, a universality class is a collection of mathematical models which share a single scale invariant limit under the process of renormalization group flow. While the models within a class may differ dramatically at finite scales, their behavior will become increasingly similar as the limit scale is approached. In particular, asymptotic phenomena such as critical exponents will be the same for all models in the class.

Some well-studied universality classes are the ones containing the Ising model or the percolation theory at their respective phase transition points; these are both families of classes, one for each lattice dimension.

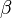
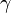
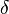
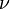
dimension	$\alpha$	$\beta$	$\gamma$	$\delta$	$\nu$	$\eta$	class
							3-state Potts
							Ashkin-Teller
							Chiral
							Directed percolation
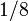
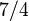
2	0	$1/8$	$7/4$		1	1/4	2D Ising
3	0.1096(5)	0.32653(10)	1.2373(2)	4.7893(8)	0.63012(16)	0.03639(15)	3D Ising
							Local linear interface
	0	$1/2$	1				Mean-field
							Molecular beam epitaxy
							Random-field
3	−0.0146(8)	0.3485(2)	1.3177(5)	4.780(2)	0.67155(27)	0.0380(4)	XY

External links

Universality classes from Sklogwiki
Zinn-Justin, Jean (2002). Quantum field theory and critical phenomena, Oxford, Clarendon Press (2002), ISBN 0-19-850923-5

This article is issued from Wikipedia - version of the Friday, February 05, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.