Unisolvent point set
In approximation theory, a finite collection of points 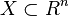 is often called unisolvent for a space
is often called unisolvent for a space 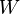 if any element
if any element 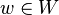 is uniquely determined by its values on
is uniquely determined by its values on  .
.
 is unisolvent for
is unisolvent for 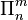 (polynomials in n variables of degree at most m) if there exists a unique polynomial in
(polynomials in n variables of degree at most m) if there exists a unique polynomial in 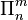 of lowest possible degree which interpolates the data
of lowest possible degree which interpolates the data  .
.
Simple examples in  would be the fact that two distinct points determine a line, three points determine a parabola, etc. It is clear that over
would be the fact that two distinct points determine a line, three points determine a parabola, etc. It is clear that over  , any collection of k + 1 distinct points will uniquely determine a polynomial of lowest possible degree in
, any collection of k + 1 distinct points will uniquely determine a polynomial of lowest possible degree in 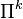 .
.
See also
External links
This article is issued from Wikipedia - version of the Wednesday, January 09, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.