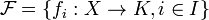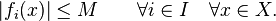Uniform boundedness

In mathematics, bounded functions are functions for which there exists a lower bound and an upper bound, in other words, a constant that is larger than the absolute value of any value of this function. If we consider a family of bounded functions, this constant can vary across functions in the family. If it is possible to find one constant that bounds all functions, this family of functions is uniformly bounded.

The uniform boundedness principle in functional analysis provides sufficient conditions for uniform boundedness of a family of operators.

Definition

Real line and complex plane

Let

\mathcal F=\{f_i: X \to K, i \in I\}

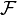be a family of functions indexed by $I$ , where $X$ is an arbitrary set and $K$ is the set of real or complex numbers. We call $\mathcal F$ uniformly bounded if there exists a real number $M$ such that

|f_i(x)|\le M \qquad \forall i \in I \quad \forall x \in X.

Metric space

In general let 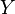$Y$ be a metric space with metric 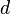$d$ , then the set

\mathcal F=\{f_i: X \to Y, i\in I\}

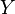is called uniformly bounded if there exists an element $a$ from $Y$ and a real number $M$ such that

d(f_i(x), a) \leq M \qquad \forall i \in I \quad \forall x \in X.

Examples

Every uniformly convergent sequence of bounded functions is uniformly bounded.

The family of functions $f_n(x)=\sin nx\,$ defined for real $x$ with $n$ traveling through the integers, is uniformly bounded by 1.

The family of derivatives of the above family, 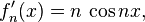$f'_n(x)=n\, \cos nx,$ is not uniformly bounded. Each 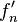$f'_n\,$ is bounded by 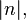$|n|,\,$ but there is no real number $M$ such that $|n|\le M$ for all integers $n.$

References

Ma, Tsoy-Wo (2002). Banach-Hilbert spaces, vector measures, group representations. World Scientific. p. 620pp. ISBN 981-238-038-8.

This article is issued from Wikipedia - version of the Friday, October 10, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.