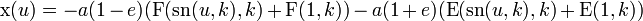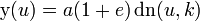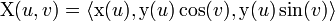Unduloid
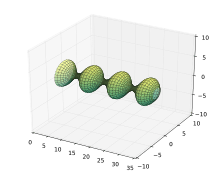
In geometry, an unduloid, or onduloid, is a surface with constant nonzero mean curvature obtained as a surface of revolution of an elliptic catenary: that is, by rolling an ellipse along a fixed line, tracing the focus, and revolving the resulting curve around the line. In 1841 Delaunay proved that the only surfaces of revolution with constant mean curvature were the surfaces obtained by rotating the roulettes of the conics. These are the plane, cylinder, sphere, the catenoid, the unduloid and nodoid.[1]
Formula
Let 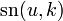 represent the normal Jacobi sine function and
represent the normal Jacobi sine function and 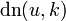 be the normal Jacobi elliptic function and let
be the normal Jacobi elliptic function and let 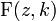 represent the normal elliptic integral of the first kind and
represent the normal elliptic integral of the first kind and 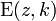 represent the normal elliptic integral of the second kind. Let a be the length of the ellipse's major axis, and e be the eccentricity of the ellipse. Let k be a fixed value between 0 and 1 called the modulus.
represent the normal elliptic integral of the second kind. Let a be the length of the ellipse's major axis, and e be the eccentricity of the ellipse. Let k be a fixed value between 0 and 1 called the modulus.
Given these variables,
The formula for the surface of revolution that is the unduloid is then
Properties
One interesting property of the unduloid is that the mean curvature is constant. In fact, the mean curvature across the entire surface is always the reciprocal of twice the major axis length: 1/(2a).
Also, geodesics on an unduloid obey the Clairaut relation, and their behavior is therefore predictable.
References
- ↑ C. Delaunay, Sur la surface de révolution dont la courbure moyenne est constante, J. Math. Pures Appl., 6 (1841), 309–320.