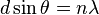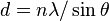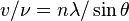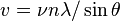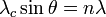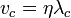Ultrasonic grating
An ultrasonic grating is a type of diffraction grating produced by interfering ultrasonic waves in a medium altering the physical properties of the medium, and hence the refractive index, in a grid-like pattern. The term acoustic grating is a more general term and can include operation at audible frequencies as well as ultrasonics.
An ultrasonic wave is a sound wave having a frequency greater than 20 kHz. The human ear cannot recognize ultrasonic waves, but animals such as bats and dogs can easily sense the ultrasonic wave. Ultrasonic waves can be produced by the Piezo-electric effect and magnetostriction.
Mechanism
When ultrasonic waves are generated in a liquid in a rectangular vessel, the wave can be reflected from the walls of the vessel. These reflected waves are called echoes. The direct and reflected waves are superimposed causing a standing wave to be formed. The density of the liquid at a node is more than the density at an antinode. Hence, the liquid acts as a diffraction grating to a parallel beam of light passed through the liquid at right angles to the wave.
The diffraction grating formed in this way is analogous to a conventional diffraction grating with lines ruled on a glass plate. The less dense antinodes refract light less and are analogous to the transmitting slits of a conventional grating. The denser nodes refract light more and are analogous to the opaque part of a conventional grating.
Mathematics
The grating element is equal to the wavelength of the ultrasonic waves. Let it be denoted by 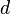 . If
. If  is the wavelength of the light passed through the grating which is diffracted by an angle
is the wavelength of the light passed through the grating which is diffracted by an angle  , then the nth order of the maximum is given by:
, then the nth order of the maximum is given by:
or
If v is the velocity of the ultrasonic wave in the liquid we can calculate the velocity of the wave with:
or,
where 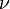 is the frequency of the wave.
is the frequency of the wave.
Debye-Sears method
The Debye-Sears method is used to determine the wavelength of monochromatic light using an acoustic or ultrasonic gratings. This method utilises the concept of piezoelectricity to obtain a grating.
The phenomenon of diffraction of light using an ultrasonic grating was first observed by Debye and Sears in 1932. When ultrasonic waves are propagated in a liquid, the density varies from layer to layer due to periodic variation of pressure. This grating can be used to determine the wavelength of monochromatic light and the speed of waves.
If 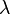 is the wavelength of a monochromatic light source, and
is the wavelength of a monochromatic light source, and 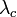 is the wavelength of the ultrasonic waves, then applying the principle of diffraction, we get
is the wavelength of the ultrasonic waves, then applying the principle of diffraction, we get
Where 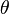 is the angle of diffraction.
is the angle of diffraction.
Thus we can calculate either 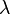 or
or 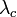 if the other is known. We need not worry about the grating element since the nodes themselves act as slits, hence the distance between two slits will be equal to the ultrasonic wave wavelength.
if the other is known. We need not worry about the grating element since the nodes themselves act as slits, hence the distance between two slits will be equal to the ultrasonic wave wavelength.
This method is used to determine the velocity of ultrasonic waves using monochromatic sources like sodium vapour lamps. The medium is usually a piezoelectric crystal such as quartz, tourmaline, or Rochelle salt. A mechanical stress is produced along an axis of the crystal using an RF oscillator. By adjusting the frequency of the oscillator, we can determine the velocity 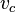 of the ultrasonic waves by using
of the ultrasonic waves by using
where 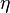 is the frequency of the oscillator.
is the frequency of the oscillator.
References
- Philip McCord Morse, "Light scattering by a sound beam", Theoretical Acoustics, pp. 809–816, Princeton University Press, 1986 ISBN 0691024014.
- Robert Lagemann, "The optical diffraction method", in Dudley Williams (ed), Molecular Physics, pp. 702–703, Academic Press, 1961 ISBN 0080859763.