UOBYQA
UOBYQA (Unconstrained Optimization BY Quadratic Approximation)[1][2][3] is a numerical optimization algorithm by Michael J. D. Powell. It is also the name of Powell's Fortran 77 implementation of the algorithm.
UOBYQA solves unconstrained optimization problems without using derivatives, which makes it a derivative-free algorithm. The algorithm is iterative, and exploits trust region technique. On each iteration, the algorithm establishes a quadratic model 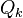 by interpolating the objective function at
by interpolating the objective function at  points, and then minimizes
points, and then minimizes 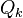 within a trust region.
within a trust region.
After UOBYQA, Powell developed NEWUOA, which also solves unconstrained optimization problems without using derivatives. In general, NEWUOA is much more efficient than UOBYQA and is capable of solving much larger problems (with up to several hundreds of variables). A major difference between them is that NEWUOA constructs quadratic models by interpolating the objective function at much less than  points (
points (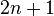 by default[4]). For general usage, NEWUOA is recommended to replace UOBYQA.
by default[4]). For general usage, NEWUOA is recommended to replace UOBYQA.
The UOBYQA software is distributed under The GNU Lesser General Public License (LGPL).[3]
See also
References
- ↑ Powell, M. J. D. (December 2000). UOBYQA: unconstrained optimization by quadratic approximation (Report). Department of Applied Mathematics and Theoretical Physics, Cambridge University. DAMTP 2000/NA14. Retrieved 2015-04-06.
- ↑ Powell, M. J. D. (2002). "UOBYQA: unconstrained optimization by quadratic approximation". Mathematical Programming, Series B (Springer) 92: 555–582. doi:10.1007/s101070100290.
- 1 2 "Source code of UOBYQA software". Retrieved 2015-04-06.
- ↑ "Source code of NEWUOA software". Retrieved 2014-01-14.
External links
- Optimization software by Professor M. J. D. Powell at CCPForge
- A repository of Professor M. J. D. Powell's software
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
